Kedudukan antara dua lingkaran atau kedudukan 2 lingkaran menunjukkan posisi antara lingkaran pertama dan lingkaran kedua. Posisi tersebut dapat berupa lingkaran di dalam lingkaran, kedua lingkaran bersinggungan di dalam lingkaran, kedua lingkaran berpotongan di dua titik, kedua lingkaran bersinggungan di luar lingkaran, atau kedua lingkaran saling lepas (tidak memiliki titik potong). Melalui halaman ini, sobat idschool akan mempelajari bagaimana kriteria kedudukan antara dua lingkaran.
Untuk menentukan posisi lingkaran pertama terhadap lingkaran kedua akan sangat mudah jika dilihat dalam gambar. Seperti halnya terlihat pada gambar di bawah. Berdasarkan gambar di atas dapat dilihat bahwa posisi lingkaran kedua berada di dalam lingkaran pertama. Namun, bagaimana jika yang diketahui hanya persamaan kedua lingkaran?

Baca Juga: Cara Mengetahui Kedudukan Titik Terhadap Lingkaran
Mencari tahu kedudukan 2 lingkaran dengan menggambarnya terlebih dahulu tentu bukan merupakan solusi yang baik. Cara ini sangat tidak efektif, sehingga tidak dianjurkan. Lalu, bagaimana cara untuk mengetahui kedudukan antara dua lingkaran yang baik? Caranya dapat dilakukan dengan memanfaatkan rumus jarak antara dua titik dan kriteria yang akan dibahas pada materi di bawah.
Table of Contents
Jarak Titik Terhadap Garis
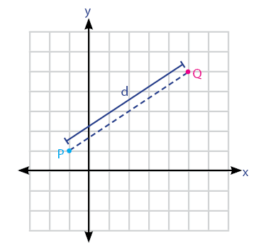
Sebelum mempelajari kedudukan antara dua lingkaran, mari kita ingat kembali rumus mengenai jarak antara dua titik. Berikut ini adalah cara atau rumus yang dapat digunakan untuk menentukan jarak antara dua titik dan jarak antara titik dan garis.
Jarak antara titik P(x1, y1) dan Q(x2, y2). Panjang titik ke garis (d) memenuhi persamaan d2 = (x1 – x2)2 + (y1 – y2)2 .
Jarak antara titik P(x1, y1) ke garis ax + by + c = 0 dapat dihitung dengan rumus dalam persamaan d berikut.
Kadua rumus di atas berguna untuk menentukan jarak antara kedua pusat lingkaran. Sehingga, kedudukan 2 lingkaran dapat diketahui melalui bentuk umum persamaan lingkarannya, tanpa harus menggambarnya terlebih dahulu.
Baca Juga: Kedudukan Garis Terhadap Lingkaran
Kriteria Kedudukan Antara Dua Lingkaran
Kedudukan antara dua lingkaran dapat diketahui melalui jarak kedua pusat lingkaran dan jumlah/selisih panjang jari-jari lingkaran. Jarak kedua pusat lingkaran dapat dihitung menggunakan rumus jarak antara dua titik seperti yang diberikan pada bahasan di atas. Sedangkan jumlah atau selilisih panjang jari-jari dapat dihitung secara langsung. Ada enam kriteria kedudukan antara dua lingkaran yang meliputi beberapa kedudukan seperti berikut.
1) Dua lingkaran memiliki titik pusat yang sama
Sebuah lingkaran memiliki pusat yang terletak di titik P1 dengan panjang jari-jari r1. Sebuah lingkaran lainnya memiliki pusat yang berada pada titik P2 dengan panjang jari-jari r2. Di mana letak titik P1 sama dengan P2 dan panjang jari-jari keduanya berbeda. Kedua lingkaran tersebut terletak pada pusat yang sama sehingga |P1 P2| = 0. Gambar kedudukan antara dua lingkaran yang memiliki titik pusat sama dan jari-jari berbeda ditunjukkan seperti berikut.
2) Bersinggungan di dalam lingkaran
Sebuah lingkaran dengan memiliki titik pusat P1 dan P2 dengan diameter r1 > r2. Jika |P1 P2| = r2 maka L1 dan L2 bersinggungan di dalam salah satu lingkaran.
3) Lingkaran kecil di dalam lingkaran besar
Suatu lingkaran memiliki titik pusat di P1 dengan panjang jari-jari r1. Suatu lingkaran lain memiliki titik pusar di P2 dengan panjang jari-jari r2. Diketahui bahwa panjang jari-jari r1 lebih besar dari panjang jari-jari r1. Jika |P1 P2| = r1 – r2 maka L2 terletak di dalam lingkaran.
4) Berpotongan di dua titik
Dua buah lingkaran memiliki letak di titik P1 dan titik P2 dengan jari-jari r1 dan r2. Jika r1 – r2 < |P1 P2| maka L1 berpotongan dengan L2 pada dua titik seperti yang ditunjukkan gambar berikut.
Baca Juga: Cara Menentukan Persamaan Lingkaran yang Diketahui Melalui Tiga Titik pada Busur Lingkaran
5) Bersinggungan di luar lingkaran (berpotongan di satu titik)
Letak titik pusat lingkaran pertama berada di titik P1 dan panjang jari-jari r1. Letak titik pusat lingkaran kedua berada di titik P2 dan panjang jari-jari r2. Jika |P1 P2| = r1 + r2 maka L1 dan L2 memiliki sebuah satu titik potong (bersinggungan).
6) Saling Lepas (Tidak Bersinggungan)
Dua buah lingkaran memiliki pusat yang terletek di titik P1 dan P2 dengan panjang jari-jari r1 dan r2. Jika jarak antara kedua pusat lingkaran |P1 P2| > r1 + r2 maka L1 dan L2 tidak bersinggugan. Gambar kedudukan antara dua lingkaran yang saling lepas (tidak bersinggungan) ditunjukkan seperti gambar berikut.
Baca Juga: Cara Menghitung Luas Segitiga Sembarang
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawa dapat sobat idschool gunakan untuk menambah pemahaman bahasan kedudukan antara dua lingkaran di atas. Setiap sontoh soal kedudukan antara dua lingkaran yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Menentukan Kedudukan Antara Dua Lingkaran
Diketahui pusat sebuah lingkaran yang terletak pada didik P1(2, 6) dengan panjang jari-jari 2 cm. dan sebuah lingkaran yang memiliki titik pusat di P2(10, 0) dengan jari-jari 6 cm. Selidikilah kedudukan antara 2 lingkaran tersebut!
Pembahasan:
Diketahui:
Letak pusat lingkaran pertama: P1 = (2, 6)
Panjang jari-jari lingkaran pertama: r1 = 2 cm
Pusat lingkaran kedua: P2 = (10, 0)
Panjang jari-jari lingkaran kedua: r2 = 6 cm
Menghitung jarak antara kedua titik pusat P1(2, 6) dan P2(10, 0):
|P1 P2|2 = (x1 – x2)2 + (y1 – x2)2
|P1 P2|2 = (2 – 10)2 + (0 – 6)2
|P1 P2|2 = (–8)2 + (–6)2
|P1 P2|2 = 64 + 36 = 100
|P1 P2| = √100 = 10 cm
Jumlah jari-jari dari kedua lingkaran:
= r1 + r2
= 2 + 6
= 8 cm
Dari hasil perhitungan diperoleh bahwa jarak antara kedua pusat lingkaran P1 dan P2 sama dengan 10 cm. Sedangkan jumlah dari kedua jari-jari lingkaran sama dengan 8 cm. Sehingga dapat disimpulkan bahwa |P1 P2| > r1 + r2 yang memberikan informasi bahwa kedua lingkaran saling bebas (tidak berpotongan atau bersinggungan).

Jadi, hubungan antara lingkaran pertama dan lingkaran kedua adalah saling lepas.
Contoh 2 – Soal Kedudukan Antara Dua Lingkaran
Diketahui pusat sebuah lingkaran yang terletak pada titik P1(2, 6) dengan panjang jari-jari 2 cm. dan sebuah lingkaran yang memiliki titik pusat di P2(10, 0) dengan jari-jari 6 cm. Selidikilah kedudukan antara 2 lingkaran tersebut!
Pembahasan:
Diketahui:
Letak pusat lingkaran pertama: P1 = (2, 6)
Panjang jari-jari lingkaran pertama: r1 = 2 cm
Pusat lingkaran kedua: P2 = (10, 0)
Panjang jari-jari lingkaran kedua: r2 = 6 cm
Menghitung jarak antara kedua titik pusat P1(2, 6) dan P2(10, 0):
|P1 P2|2 = (x1 – x2)2 + (y1 – x2)2
|P1 P2|2 = (2 – 10)2 + (0 – 6)2
|P1 P2|2 = (–8)2 + (–6)2
|P1 P2|2 = 64 + 36 = 100
|P1 P2| = √100 = 10 cm
Jumlah jari-jari dari kedua lingkaran:
= r1 + r2
= 2 + 6
= 8 cm
Dari hasil perhitungan diperoleh bahwa jarak antara kedua pusat lingkaran P1 dan P2 sama dengan 10 cm. Sedangkan jumlah dari kedua jari-jari lingkaran sama dengan 8 cm. Sehingga dapat disimpulkan bahwa |P1 P2| > r1 + r2 yang memberikan informasi bahwa kedua lingkaran saling bebas (tidak berpotongan atau bersinggungan).
Sekian ulasan tentang kedudukan antara dua lingkaran yang meliputi dua lingkaran dengan pusat yang sama, bersinggungan di dalam lingkaran, lingkaran kecil terletak di dalam lingkaran besar, dua lingkaran berpotongan pada dua titik, dua lingkaran bersinggungan di luar lingkaran, dan dua lingkaran yang saling lepas (tidak memiliki titik potong. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.