Perbedaan cross product dan dot product terdapat pada hasil akhir atau product operasi perkalian. Untuk perkalian dua vektor dengan cross product akan menghasilkan sebuah vektor. Sementara perkalian dua vektor dengan dot product akan menghasilkan sebuah skalar. Vektor adalah besaran yang memiliki nilai dan arah, sedangkan skalar adalah besaran yang hanya memiliki nilai (tidak memiliki arah).
Cross product pada perkalian vektor disimbolkan dengan tanda silang (×), misalnya vektor a × b. Sedangkan dot product pada operasi perkalian vektor dimbolkan dengan titik gemuk atau dot fat (•).
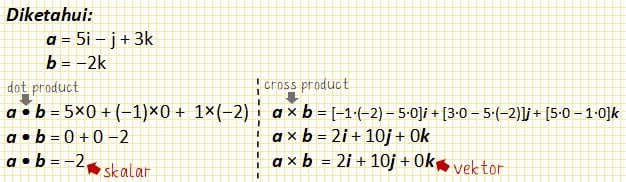
Perbedaan cross product dan dot product terdapat pada saat melakukan operasi perkalian dua buah vektor. Untuk operasi perkalian sebuah vektor A dengan suatu skalar k disebut perkalian langsung (direct product). Hasil perkalian vektor A dengan skalar k adalah sebuah tensor atau matriks B yang memenuhi persamaan B = kA.
Apa saja perbedaan cross product dan dot product dalam proses perkalian vektor? Bagaimana cara melakukan operasi perkalian vektor untuk cross product? Bagaimana cara melakukan operasi perkalian vektor untuk dot product? Sobat idshcool dapat mencari tahu jawabannya melalui ulasan perbedaan cross product dan dot product di bawah.
Table of Contents
Baca Juga: Cara Menentukan Vektor Satuan
Bentuk Opearasi Cross Product dan Dot Product
Vektor merupakan obyek geometri yang disimbolkan melalui sebuah anak panah. Pangkal anak panah adalah koordinat titik awal vektor dan ujung anak panah adalah koordinat titik akhir vektor. Misalkan diketahui koordinat titik A(x1, y1, z1) dan B(x2, y2, z2) maka vektor AB sama dengan AB = (x2 ‒ x1, y2 ‒ y1, z2 ‒ z1).
Dua buah vektor dapat dilakukan operasi perkalian vektor yang dapat menghasilkan sebuah vektor atau skalar. Operasi perbedaan cross product dan dot product pada perkalian vektor dengan vektor terdapat pada bahasan berikut.
1) Operasi Perkalian Cross Product
Pada operasi cross product (perkalian silang) atau vector product (produk vektor) ditandai dengan penggunaan simbol ×. Di mana simbol × terletak diantara dua buah vektor yang diperasikan. Hasil dari operasi cross product adalah sebuah vektor baru. Mengutip dari Math is Fun, hasil vektor baru pada operasi cross product memiliki arah tegak lurus dengan kedua vektor yang dioperasikan.
Contoh penerapan perkalian silang terdapat pada persamaan rumus torsi (τ) atau momen gaya yaitu τ = F × r dengan F adalah gaya dan r adalah perpindahan. Diketahui bahwa gaya (F) dan perindahan (r) adalah besaran vektor, begitu juga dengan momen gaya (torsi) adalah besaran vektor. Sehingga dapat dikatakan bahwa bentuk operasi perkalian pada rumus torsi adalah cross product.
Secara ringkas, aturan operasi perkalian vektor dengan cross product terdapat pada daftar berikut.

Contoh operasi perkalian vektor dengan cross product:
a = 5i ‒ j + 3k
b = ‒2k
a × b = [‒1·(‒2) ‒ 5·0]i + [3·0 ‒ 5·(‒2)]j + [5·0 ‒ 1·0]k
a × b = 2i + 10j + 0k = 2i + 10j + 0k
2) Operasi Perkalian Dot Product
Opeasi dot Product (perkalian titik) atau scalar product (produk skalar) ditandai dengan penggunaan simbol • diantara vektor yang dioperasikan. Hasil dari perkalian vektor dengan dot product adalah sebuah skalar (hanya memiliki nilai).
Contoh penerapan perkalian titik terdapat pada persamaan usaha (W) yaitu perkalian gaya (F) dan perpindahan (s). Diketahui bahwa gaya (F) dan perpindahan (s) merupakan besaran vektor, sedangkan usaha (W) adalah besaran skalar. Sehingga bentuk operasi perkalian pada rumus usaha W = F · s merupakan dot product.
Secara ringkas, aturan operasi perkalian vektor dengan dot product terdapat pada daftar berikut.

Contoh operasi perkalian vektor dengan dot product:
a = 5i ‒ j + 3k
b = ‒2k
a • b = 5×0 + (‒1)×0 + 1×(‒2)
a • b = 0 + 0 ‒ 2 = ‒2
Baca Juga: Vektor yang Saling Tegak Lurus dan Sejajar
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan cross product dan dot product di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana pernggunaan cross product dan dot product. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Perbedaan cross product dan dot product
Diketahui dua buah vektor adalah F1 = 60 N dan F2 = 80 N memiliki titik tangkap sama. Jika dot product untuk kedua vektor sama dengan 240 N maka besar sudut apit antara dua vektor tersebut adalah ….
A. 30o
B. 45o
C. 60o
D. 90o
E. 120o
Pembahasan:
Besar sudut apit yang dibentuk oleh vektor F1 dan F2 dapat dicari tahu melalui persamaan dot product dari F1 dan F2 seperti berikut.
F1 · F2 = |F1 || F2|cos θ
240 = 60 × 80 × cos θ
240 = 480 × cos θ
Cos θ = 240/480 = 1/2
θ = 60o
Jadi, besar sudut apit antara dua vektor tersebut adalah 60o.
Jawaban: C
Contoh 2 – Perbedaan cross product dan dot product
Sebuah gaya F = 3i + 4k N digunakan untuk membuka sekrup dengan poisisi r = (‒0,3; 0; 0,4) m. Besar momen gaya yang memengaruhi gaya tersebut adalah ….
A. 2,4 Nm
B. 1,2 Nm
C. 0,8 Nm
D. 0,6 Nm
E. 0,4 Nm
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh beberapa informasi dua vektor berikut.
- Gaya: F = 3i + 4k
- Posisi: r = ‒0,3i + 0,4k
Momen gaya memiliki persamaan cross product antara gaya dan posisi, atau secara matematis dituliskan τ = F × r. Cara menentukan vektor momen gaya atau torsi (τ) dilakukan seperti cara berikut.
Vektor momen gaya atau torsi (τ): τ = F × r
τ = (3i + 4k) × (‒0,3i + 0,4k)
τ = [0.4 ‒ 0,4·0]i + [0,4·3 ‒ (‒0,3)·4]j + [(‒0,3)·0 ‒ 0·3]k
τ = (0 ‒ 0)i + (1,2 + 1,2)j + (0 ‒ 0)k = 2,4j
Besar momen gaya:|τ| = √(2,4)2 = 2,4 Nm
Jadi, besar momen gaya yang memengaruhi gaya tersebut adalah 2,4 Nm.
Jawaban: A
Contoh 3 – Perbedaan cross product dan dot product
Sebuah balok berada pada bidang datar licin ditarik oleh gaya 200 N dengan arah membentuk sudut 60o terhadap arah horisontal.

Pada saat balok berpindah 8 m, besar usaha yang dilakukan oleh gaya F adalah ….
A. 200 joule
B. 400 joule
C. 800 joule
D. 1.200 joule
E. 1.600 joule
Pembahasan:
Berdasarkan informasi yang diberikan pada soal dapat diketahui bahwa,
- Besar nilai vektor dari gaya: F = 200 N
- Besar nilai vektor perpindahan: s = 8 m
- Sudut yang dibentuk kedua vektor: θ = 60o
Usaha didefinisikan sebagai perkalian gaya (F) yang bekerja selama perpindahan (s). Gaya dan perpindahan merupakan besaran vektor, sementara usaha merupakan besaran skalar. Besar usaha yang dilakukan gaya F dapat dihitung seperti cara berikut.
W = Fx · s
W = F cos 60o · s
W = 200 × 1/2 × 8
W = 800 joule
Jadi, besar usaha yang dilakukan oleh gaya F pada saat balok berpindah 8 m adalah 800 joule.
Jawaban: C
Demikianlah tadi ulasan bagaimana bentuk operasi pada perbedaan cross product dan dot product. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Hitung Resultan Vektor 3 Arah Secara Analisis
