Vektor satuan adalah vektor yang besarnya sama dengan satu dan arahnya sama dengan vektornya. Cara mencari vektor satuan diperoleh melalui koordinat vektor dan panjang vektor tersebut. Simbol vektor satuan dituliskan dengan tanda seperti topi yang disebut caret (^) di atas huruf. Bahasan vektor satuan cukup penting untuk dipahami karena merupakan dasar untuk mempelajari bahasan vektor selanjutnya seperti dot products vector, cross products vector, dan lain sebagainya.
Vektor sendiri merupakan besaran yang memiliki nilai dan arah. Arah vektor dapat ke kanan, kiri, bawah, atas, atau dinyatakan dengan sudut α, di mana α adalah sudut terkecil yang dibentuk vektor dengan sumbu x. Cara menuliskan vektor dapat dituliskan melalui panjang dan arah berupa besar sudutnya. Contohnya sebuah vektor dengan panjang 3 satuan membentuk sudut 30o.
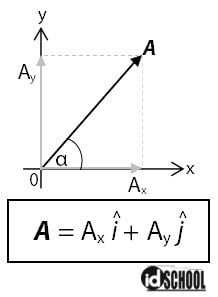
Sebuah vektor A yang terletak pada dimensi dua atau bidang xy dengan sudut α dapat diproyeksikan menjadi komponen Ax dan Ay. Komponen vektor A pada sumbu x adalah Ax dan komponen vektor pada sumbu y adalah Ay. Panjang vektor Ax = A cos α dan panjang vektor Ay = A sin α. Penjumlahan vektor Ax dan Ay merupakan vektor A, sehingga berlaku persamaan A = Axi + Ayj.
Bentuk vektor yang dinyatakan seperti pada komponen vektor A memuat vektor satuan i – j – k.
Baca Juga: Cara Menghitung Panjang Vektor AB
Apa itu vektor satuan i – j – k? Bagaimana cara mencari vektor satuan? Sobat idschool dapat mencari lebih lanjut melalui bahasan di bawah.
Table of Contents
Hubungan Antara Vektor Satuan dan Panjang Vektor
Pada bagian awal telah disinggung bahwa vektor satuan adalah vektor dengan arah sama yang memiliki panjang satu satuan. Misalkan sebuah vektor v memiliki nilai tiga satuan ke kanan, maka vektor satuan v adalah vektor dengan arah yang sama dengan vektor v yaitu ke kanan tetapi miliki panjang satu. Vektor v akan bernilai satu ketika dikalikan dengan skalar k = 1/3, sehingga vektor satuan v sama dengan 1/3 vektor v.
Secara umum, agar suatu vektor memiliki panjang satu satuan maka perlu dikalikan dengan sebuah skalar yang nilainya satu per panjang vektor tersebut. Kesimpulannya, terdapat hubungan antara vektor satuan dan panjang vektor yang dapat dinyatakan dalam sebuah persamaan. Hubungan tersebut dinyatakan melalui persamaan yang dapat digunakan sebagai cara mencari vektor satuan seperti berikut.
Contoh bagaimana cara mencari vektor satuan dapat dilihat pada penyelesaian contoh soal berikut.
Soal:
Tentukan vektor satuan dari vektor p = (4, –3, 0)!
Penyelesaian:
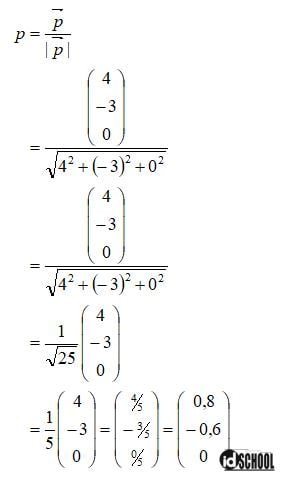
Komponen vektor dalam koordinat disepakati dengan penyimbolan vektor satuan untuk sumbu x, sumbu y, dan sumbu z. Vektor satuan pada sumbu x positif yaitu satu satuan ke kanan disimbolkan dengan huruf i. Vektor satuan pada sumbu y positif atau satu satuan ke atas disimbolkan dengan huruf j. Sedangkan vektor satuan yang searah dengan sumbu z positif disimbolkan dengan huruf k.
Komponen sebuah vektor dalam sebuah kesepakatan akan bernilai positif jika komponen tersebut berada pada sumbu x, sumbu y, dan sumbu z positif. Sebaliknya, komponen sebuah vektor bernilai negatif jika komponen tersebut berada pada sumbu x, y, dan z negatif.
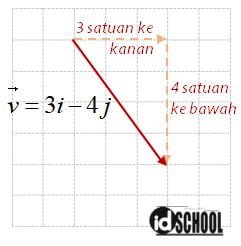
Berdasarkan kesepakatan tersebut, maka vektor v yang dinyatakan dalam persamaan vektor v = 3i – 4j dapat secara mudah dimengerti. Vektor v = 3i – 4j sama dengan vektor dengan arah tiga satuan ke kanan (sejajar sumbu x) dilanjutkan empat ke bawah (sejajar sumbu y). Dengan demikian, vektor satuan akan memudahkan dalam menjelaskan arah dan mengidentifikasi komponen vektor dalam bahasan vektor.
Baca Juga: Cara Menghitung Resultan Vektor 3 Arah Secara Analisis
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan sebagai tolak ukur keberhasilan memahami bahasan cara mencari vektor satuan di atas. Setiap contoh soal yang diberikan disertai dengan pembahasan cara mencari vektor satuan. Sobat idschool dapat menggunakan pembahasan tersebut untuk mengetahui keberhasilan dalam mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal Penulisan Vektor Satuan
Perhatikan gambar berikut!
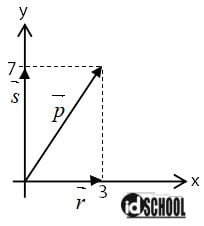
Vektor satuan pada vektor p dapat dituliskan ke dalam persamaan ….
A. 3i + 5j
B. 3i + 7j
C. 5i + 7j
D. 7i + 3j
E. 7i + 7j
Pembahasan:
Vektor p merupakan vektor dengan arah tiga satuan ke kanan dan 7 satuan ke atas. Sehingga, vektor satuan pada vektor v dapat dituliskan ke dalam persamaan p = 3i + 7j.
Jawaban: B
Contoh 2 – Soal Cara Mencari Vektor Satuan

Pembahasan:
Mencari vektor satuan v:

Jawaban: B
Contoh 3 – Soal Cara Mencari Vektor Satuan
Diketahui koordinat titik P (2, –1, 3) dan Q (3, –3, 5). Vektor satuan yang searah degab vektor PQ adalah ….
A. i + 2j + 2k
B. i – 2j + 2k
C. 1/3i + 2/3j + 2/3k
D. 1/3i – 2/3j + 2/3 k
E. –1/3i + 2/3j – 2/3 k
Pembahasan:
Mencari komponen vektor PQ:
Vektor PQ = Q – P
= (3, –3, 5) – (2, –1, 3)
= (3 – 2, –3 –(–1), 5 – 3)
= (1, –3 +1, 2)
= (1, –2, 2)
Mencari vektor satuan yang searah dengan vektor PQ:
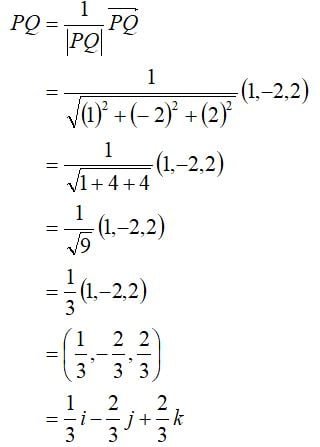
Jadi, vektor satuan yang searah dengan vektor PQ adalah 1/3i – 2/3j + 2/3 k.
Jawaban: D
Demikianlah tadi ulasan materi cara mencari vektor satuan yang meliputi apa itu vektor satuan dan apa pentingnya memahami bahasan vektor satuan pada bahasan vektor selanjutnya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Perkalian Silang Vektor (Cross Product Vector: a x b)