Kedudukan dua buah vektor berdasarkan sudut yang dibentuk dapat saling tegak lurus atau saling sejajar. Vektor yang saling tegak lurus akan membentuk sudut 90o (siku-siku). Sedangkan vektor yang saling sejajar akan membentuk sudut 0o atau akan dapat berhimpitan pada satu garis (kolinear). Vektor yang memiliki arah yang sama biasanya disimbolkan dengan tanda positif (+), sementara dua buah vektor yang saling berkebalikan ditandai dengan simbol negatif (-).
Vektor sendiri merupakan objek geometri yang digambarkan dengan simbol anak panah. Vektor memiliki nilai dan arah sehingga vektor dengan nilai yang sama dan arah yang berbeda merupakan vektor yang berbeda. Sebuah vektor dikatakan sama jika memiliki nilai dan arah yang sama.
Sebagai contoh, sebuah vektor memiliki panjang 3 satuan dengan arah ke kanan dan sebuah vektor yang memiliki panjang 3 satuan dengan arah ke kiri. Kedua vektor tersebut memiliki nilai panjang yang sama namun arah yang berbeda. Kesimpulannya, dua buah vektor tersebut merupakan dua vektor yang berbeda.
Dua buah vektor dapat membentuk suatu sudut sehingga dapat berkedudukan sebagai vektor yang saling tegak lurus atau vektor yang saling sejajar. Bagaimana cara menentukan vektor yang saling tegak lurus ? Bagaimana cara menentukan vektor yang saling sejajar? Sobat idschool dapat mencari tahu jawabannya melalui vektor yang saling tegak lurus dan sejajar melalui ulasan di bawah.
Table of Contents
- Kedudukan 2 Vektor yang Saling Tegak Lurus dan Sejajar
- Operasi Perkalian Vektor x Vektor
- Contoh Soal dan Pembahasan
Baca Juga: Cara Menghitung Panjang Vektor AB
Kedudukan 2 Vektor yang Saling Tegak Lurus dan Sejajar
Diketahui dua buah vektor a dan b yang mana kedua ujungnya dapat membentuk suatu besar sudut α. Jika besar sudut yang dibentuk sama dengan sudut siku-siku (α = 90o) maka kedudukan dua vektor saling tegak lurus. Sedangkan jika besar yang dibentuk adalah α = 0o maka kedudukan dua vektor saling sejajar.
Kedudukan dua vektor yang saling tegak lurus dan vektor yang saling sejajar berhubungan dengan operasi perkalian vektor. Di mana opersai perkalian vektor a dan vektor b memenuhi persamaan a · b = |a||b| · α dengan |a| adalah panjang vektor a, |b| adalah panjang vektor b, dan α adalah sudut yang dibentuk kedua vektor teresebut.
Diketahui bahwa nilai cos 0o = 1 dan cos 90o = 0, sehingga dapat diperoleh persamaan umum untuk vektor yang saling tegak lurus dan sejajar seperti berikut.
- Vektor a dan vektor b merupakan dua vektor saling sejajar:
a · b = |a||b| · cos 0o
a · b = |a||b|
- Vektor a dan b merupakan dua vektor yang saling tegak lurus:
a · b = |a||b| · cos 90o
a · b = 0.
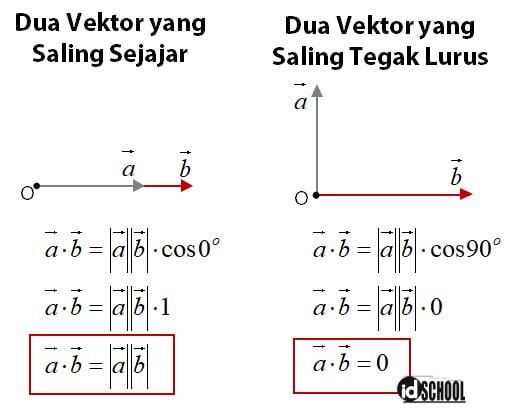
Persamaan untuk vektor yang saling tegak lurus dan sejajar memenuhi hasil kali dua vektor seperti keterangan pada gambar di bawah.
Baca Juga: Operasi Perkalian Vektor
Operasi Perkalian Vektor x Vektor
Ada dua jenis perkalian vektor berdasarkan product atau hasli akhirnya yaitu cross product (perkalian cross) dan dot product (perkalian dot). Di mana cross product dan dot product memiliki aturan yang berbeda dalam langkah melakukan operasi perkalian vektor. Perbedaan dari kedua bentuk perkalian vektor tersebut dijelaskan melalui masing-masing ulasan beriku.
1) Cross Product [Perkalian silang]: a × b
Cross Product atau vector product (produk vektor) merupakan perkalian vektor dengan vektor yang menghasilkan vektor. Dengan kata lain, hasil akhir dari perkalian silang menghasilkan besaran yang memiliki nilai dan arah (vektor). Simbol untuk perkalian dari cross product adalah tanda silang atau cross (×) diantara dua vektor yang dikalikan.
Cara mengalikan operasi perkalian vektor dengan vektor untuk cross product:
- a × b = c
- a × b = |a||b|sin α n^
- a × b = cxi + cxj + cxk
- a × b = ‒b× a
- a × (b + c) = a × b + a × c
- a × a = 0
Misalkan, perkalian cross antara vektor a dan vektor b menghasilkan sebuah vektor c, atau secara matematis dituliskan a × b = c. Arah vektor c yang dihasilkan dari perkalian cross merupakan vektor yang tegak lurus terhadap vektor a dan vektor b.
Sebagai contoh, perkalian vektor a = 2i – 3j + k dan vektor b = i + 4j – 2k menghasilkan vektor c = 2i + 5j + 11k. Cara melakukan operasi perkalian antara vektor a dan vektor b terdapat seperti penyelesaian contoh berikut.

2) Dot Product [Perkalian Titik]: a • b
Dot Product disebut juga produk skalar (scalar product) atau perkalian titik yang biasanya disimbolkan dengan titik gemuk (fat dot) sebagai tanda operasi perkalian vektor. Di mana operasi perkalian titik adalah operasi perkalian antar vektor yang menghasilkan besaran skalar (nilai tanpa arah).
Cara mengalikan operasi perkalian vektor dengan vektor untuk dot product:
- a · b = c
- a · b = |a||b| cos α
- a · b = axbx + ayby + azbz
- a · b = b · a
- a · a = (a)2
- a · (b + c) = a · b + b · c
Contoh operasi perkalian dot:
a = 2i – 3j + k
b = i + 4j – 2k
a • b = (2 · 1)i + (–3 · 4)j + (1 · –2)k
a • b = 2i – 12j –2k
Baca Juga: 4 Metode Penjumlahan Vektor
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk mengasah kemampuan untuk materi bahasan vektor yang saling tegak lurus dan sejajar. Setiap contoh soal vektor yang saling tegak lurus dan sejajar dilengkapi dengan pembahasan soalnya. Sobat idschool dapat menggunakannya sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal Vektor yang Saling Tegak Lurus
Diketahui dua vektor a = (2, –5, 1) dan b =(x, –2, 4) saling tegak lurus. Nilai x dari vektor b adalah ….
A. –14
B. –7
C. 0
D. 7
E. 14
Pembahasan:
Vektor yang saling tegak lurus memenuhi persamaan: a · b = 0, sehingga nilai x pada vektor b dapat dicari dengan cara berikut.

Jadi, nilai x dari vektor b adalah –7.
Jawaban: B
Contoh 2 – Soal Vektor yang Saling Tegak Lurus
Diketahui vektor a = i + 2j – xk, b = 3i – 2j + k, dan c = 2i + j + 2k. Jika vektor a tegak lurus vektor c, hasil kali vektor (a + b)(a – c) adalah ….
A. –4
B. –2
C. 0
D. 2
E. 4
Pembahasan:
Diketahui bahwa vektor a tegak lurus dengan vektor c sehingga memenuhi persamaan a · c = 0. Besar dan arah vektor a = i + 2j – xk = (1, 2, – x) dan vektor c = 2i + j + 2k = (2, 1, 2) sehingga dapat diperoleh nilai x seperti berikut.

Diperoleh nilai x = 2, maka vektor a = i + 2j – 2k
Mencari hasil kali vektor (a + b)(a – c):
(a + b)·(a – c) = (1+3, 2+(–2), –2+1) · (1 – 2, 2 – 1, – 2 – 2)
= (4, 0, –1) · (–1, 1, –4)
= 4(–1) + 0(1) + (–1)(–4)
= 0
Jadi, hasil kali vektor (a + b)(a – c) adalah 0.
Jawaban: C
Baca Juga: Perbandingan Dalam Vektor dan Perbandingan Luar Vektor
Contoh 3 – Soal Vektor yang Saling Tegak Lurus

Pembahasan:
Diketahui besar dan arah vektor-vektor a, b, dan c, seperti berikut.
- a = 3i – 2j + 4k = (3, –2, 4)
- b = 4i + 3j + 5k = (4, 3, 5)
- c = 2i + xj – 4k = (2, x, –4)
Diketahui bahwa vektor a tegak lurus vektor c sehingga memenuhi persamaan a · c = 0. Bilangan x pada vektor c dapat diperoleh seperti cara berikut.
a · c = 0
(3, –2, 4) · (2, x, –4) = 0
3 · 2 + (–2) · x + 4 · –4 = 0
6 –2x – 16 = 0
–2x = 16 – 6
–2x = 10
x = 10/–2 = –5
Berdasarkan perhitungan di atas dapat diperoleh bilangan x pada vektor c adalah x = –5. Sehingga, besar dan arah vektor c = (2, –5, –4), selanjutnya adalah menentukan hasil dari 2a + b – c.
2a + b – c = 2(3, –2, 4) + (4, 3, 5) – (2, –5, –4)
2a + b – c = (6, –4, 8) + (4, 3, 5) – (2, –5, –4)
= (6 + 4 – 2, –4 + 3 – (–5), 8 + 5 – (–4))
= (6 + 4 – 2, –4 + 3 +5, 8 + 5 + 4) = (8, 4, 17)
Hasil operasi 2a + b – c = (8, 4, 17) yang dapat dinyatakan dalam bentuk 8i + 4j + 17k. Jadi, hasil dari 2a + b – c adalah 8i + 4j + 17k.
Jawaban: E
Contoh 4 – Soal Vektor yang Saling Sejajar
Diketahui titik-titik A(3, 2, –1), B(1, –2, 1), dan C(7, p – 1, –5) segaris untuk nilai p = ….
A. 13
B. 11
C. 5
D. –11
E. –13
Pembahasan:
Titik A, B, dan C terletak segaris sehingga memenuhi persamaan AB = k AC dengan k merupakan suatua konstanta skalar.

Menentukan nilai k:
–2 = k · 4
k =–2/4
k =–1/2
Menghitung nilai p:
–4 = k(p – 3)
–4 = –1/2(p – 3)
p – 3 = –4 × –2
p – 3 =8
→ p = 8 + 3 = 11
Jadi, titik-titik A(3, 2, –1), B(1, –2, 1), dan C(7, p – 1, –5) segaris untuk nilai p = 11.
Jawaban: B
Demikianlah tadi ulasan materi vektor yang saling tegak lurus dan sejajar. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menghitung Resultan Vektor 3 Arah Secara Analitis
