Cara Menentukan Nilai Limit Fungsi Trigonometri

Ada beberapa hal yang perlu diperhatikan pada cara menentukan nilai limit fungsi trigonometri. Hal yang perlu diperhatikan antara lain adalah bagaimana nilai x yang mendekatinya. Apakah nilai limit fungsi dengan x mendekati tak hingga, nilai limit fungsi dengan x mendekati suatu nilai, atau nilai limit pada fungsi dengan x mendekati 0. Karakteristik dari limit fungsi trigonometri memuat fungs-fungsi trigonometri seperti fungsi sin, cos, tan, dan fungsi turunan lainnya.

Variasi soal tentang limit fungsi trigonometri sangat banyak yang dapat diselesaikan dengan metode/teknik tertentu untuk setiap bentuk variasi soal. Keterampilan cara menentukan nilai limit fungsi trigonometri akan terasah dengan banyak mengerjakan latihan soal tentang limit fungsi trigonometri. Melalui halaman ini pula sobat idschool dapat memperdalam pengetahuan materi limit fungsi trigonometri yang meliputi bahasan limit fungsi trigonometri untuk x mendekati suatu bilangan dan x mendekati nol.

Bagaimana cara menentukan nilai limit fungsi trigonometri? Sobat idschool dapat mencari tahu jawabannya melalui bahasan cara menentukan nilai limit fungsi trigonometri di bawah.

Table of Contents

• Limit Fungsi Trigonometri untuk x Mendekati Suatu Bilangan
• Limit Fungsi Trigonometri untuk x Mendekati 0 (Nol)
• Contoh Soal dan Pembahasan
  • Contoh 1 – Soal Limit Trigonometri
  • Contoh 2 – Soal Limit Trigonometri

Limit Fungsi Trigonometri untuk x Mendekati Suatu Bilangan

Cara menentukan nilai limit fungsi trigonometri untuk x mendekati suatu bilangan c dapat secara mudah diperoleh dengan melakukan substitusi nilai c pada fungsi trigonometrinya. Misalnya, untuk nilai limit fungsi trigonometri sin x dengan x mendekati c maka nilai limitnya sama dengan sin c.

Begitu juga untuk nilai limit fungsi trigonometri cos x dan tan x pada limit nilai x mendekati c maka nilai limitnya sama dengan cos c dan tan c.

Secara umum. persamaan rumus limit fungsi trigonometri diberikan seperti berikut.

Berikut ini adalah contoh soal penggunaan rumus limit fungsi trigonometri untuk x mendekati suatu bilangan.

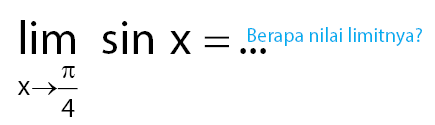
Pembahasan:
Substitusi nilai x = ^π/₄ pada persamaan fungsi sinus, sehingga dapat diperoleh nilai limit seperti yang ditunjukkan seperti berikut.

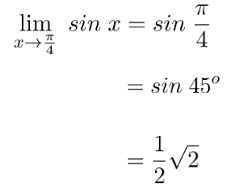
Baca Juga: Pengertian Limit

Limit Fungsi Trigonometri untuk x Mendekati 0 (Nol)

Pada kasus tertentu, nilai limit untuk x mendekati bilangan 0 yang akan menghasilkan 0/0. Kondisi tersebut akan terjadi jika dilakukan substitusi secara langsung, misalnya pada kasus berikut.

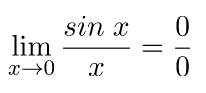
Sebagaimana yang kita tahu bahwa nilai limit tersebut bukan nilai limit yang diharapkan. Kita perlu menggunakan metode lain untuk mendapatkan nilainya.

Dalam pembahasan cara menentukan limit fungsi trigonometri, terdapat berbagai rumus yang dapat disebut sebagai “properti” untuk menyelesaikan soal limit fungsi trigonometri. Kumpulan properti tersebut dapat dilihat pada daftar rumus limit trigonometri yang diberikan di bawah.

Mungkin, beberapa dari sobat idschool akan bertanya, dari mana properti yang terangkum dalam persamaan di atas diperoleh. Sebenarnya, hasil dari persamaan – persamaan itu diperoleh menggunakan definisi limit dan teorema limit yang sudah ada.

Untuk tingkat Sekolah Menengah Atas, sobat idschool hanya perlu mengetahui properti yang dapat digunakan pada cara menentukan nilai limit fungsi trigonometri pada suatu soal.

Penjelasan dari mana persamaan di atas diperoleh akan diberikan di tingkat lanjut, jika kalian tertarik untuk mengambil matematika sebagai studi lanjutan yang biasanya diberikan di perguruan tinggi.

Selanjutnya, mari simak contoh cara menggunakan nilai limit trigonometri menggunakan properti yang diberikan di atas.

Perhatikan soal di bawah!

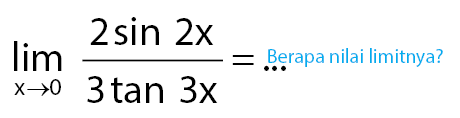
Pembahasan:
Cara menggunakan properti rumus limit fungsi trigonometri dapat dilihat pada proses pengerjaan cara menentukan nilai limit fungsi trigonometri berikut.

Dengan mudah, kita dapat mendapatkan nilai limit fungsi trigonometri yang diberikan pada soal adalah ⁴/₉.

Baca Juga: Limit tak Hingga

Contoh Soal dan Pembahasan

Beberapa contoh soal dan pembahasan di bawah akan meningkatkan pemahaman sobat idschool terkait bagaimana cara menentukan limit fungsi trigonometri. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya yang dapat digunakan sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Soal Limit Trigonometri

Nilai limit fungsi trigonometri di atas adalah …..
A. ¹/₄
B. ¹/₂
C. ³/₄
D. 1
E. 1¹/₄

Pembahasan:
Nilai limit fungsi trigonometri tersebut dapat diselesaikan dengan cara berikut.

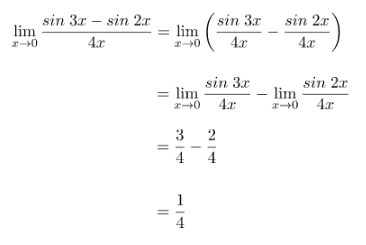
Jadi, nilai limit fungsi trigonometri di atas adalah ¹/₄

Jawaban: A

Baca Juga: 7 Tips Menyelesaikan Limit Fungsi di Suatu Titik

Contoh 2 – Soal Limit Trigonometri

Nilai limit fungsi trigonometri di atas adalah ….
A. 8
B. 4
C. 0
D. ‒4
E. ‒8

Pembahasan:
Nilai limit trigonometri pada soal yang diberikan dapat ditentukan melalui cara berikut.

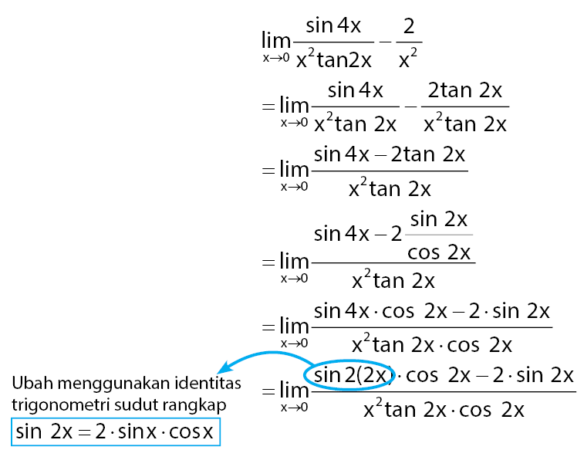
Dengan melakukan transformasi menggunakan identitas trigonometri rumus fungsi sinus sudut rangkap akan diperoleh persamaan di bawah.

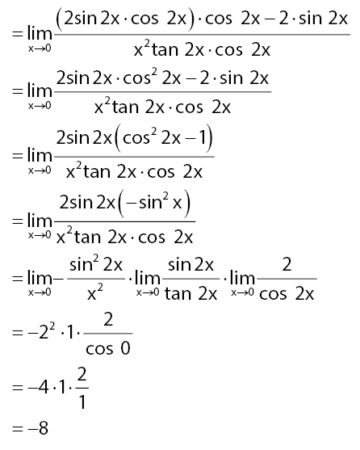
Jadi, nilai limit fungsi trigonometri di atas adalah ‒8.

Jawaban: E

Sekian pembahasan bagaimana cara menentukan nilai limit fungsi trigonometri yang meliputi nilai limit mendekati suatu bilangan dan nilai limit mendekati nol. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Kumpulan Soal Limit Fungsi Trigonometri