Persamaan kuadrat adalah bentuk persamaan yang ditandai melalui pangkat tertinggi variabelnya sama dengan dua. Bentuk umum persamaan kuadrat dinyatakan melalui y = ax2 + bx + c dengan a, b, dan c merupakan suatu bilangan. Persamaan kuadrat dapat memiliki dua akar real berbeda, dua akar real kembar, atau imaginer (akar-akar tidak real).
Sayarat agar persamaan kuadrat mempunyai dua akar real adalah memiliki nilai diskriminan positif (D > 0). Sementara agar persamaan kuadrat mempunyai akar real kembar/sama adalah memiliki nilai diskriminan sama dengan nol (D = 0). Dan untuk syarat agar persamaan kuadrat mempunyai akar-akar tidak real adalah memiliki nilai diskrimianan negatif (D < 0).

Baca Juga: Langkah-Langkah Menggambar Grafik Fungsi Kuadrat
Bagaimana bentuk persamaan kuadrat agar mempunyai dua akar real? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Hubungan Nilai Diskriminan dengan Banyaknya Akar pada Persamaan Kuadrat
- Contoh Penggunaan Syarat Agar Persamaan Kuadrat Mempunyai Dua Akar Real
- Contoh Soal dan Pembahasan
Hubungan Nilai Diskriminan dengan Banyaknya Akar pada Persamaan Kuadrat
Diskriminan biasanya disimbolkan dengan huruf D adalah besaran yang dapat digunakan untuk membedakan jenis akar persamaan kuadrat. Jenis akar persamaan kuadrat dapat berupa akar-akar real atau akar-akar imaginer (tidak real).
Nilai diskriminan untuk persamaan kuadrat ax2 + bx + c = 0 adalah D = b2 ‒ 4ac. Hasil perhitungan nilai diskriminan dapat digunakan untuk mengetahui jenis akar-akar dari suatu persamaan kuadrat.
- Jika nilai diskriminan lebih besar atau sama dengan nol maka persamaan kuadrat mempunyai akar-akar real.
- Jika nilai diskriminan negatif atau kurang dari nol maka akar-akar persamaan kuadrat tidak real (imajiner). Bilangan imajiner terdapat pada akar dari bilangan negatif.
1) Diskriminan Negatif (D < 0)
Sebagai contoh, persamaan kuadrat 2x2 ‒ 4x + 9 = 0 memiliki nilai diskriminan sama dengan D = (‒4)2 ‒ 4(2)(9) = 16 ‒ 72 = ‒56. Dapat diperoleh nilai diskriminan persamaan kuadrat 2x2 ‒ 4x + 9 = 0 adalah D = ‒56.
Nilai diskriminan D = ‒56 dapat memberikan informasi bahwa akar-akar dari persamaan kuadrat 2x2 ‒ 4x + 9 = 0 adalah bilangan imaginer. Atau dapat dikatakan bahwa persamaan kuadrat 2x2 ‒ 4x + 9 = 0 tidak memiliki akar-akar dalam himpunan bilangan real.
Untuk lebih meyakinkan, perhatikan hasil dari penyelesaian cara untuk mendapatkan akar-akar persamaan kuadrat 2x2 ‒ 4x + 9 = 0 di bawah.

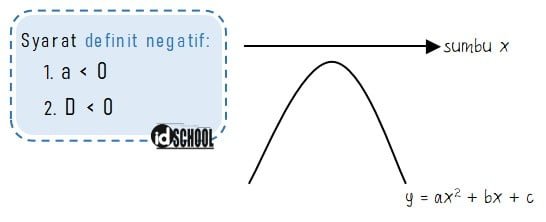
Persamaan kuadrat dengan nilai diskriminan negatif (D < 0) jika digambarkan akan menghasilkan kurva yang tidak mempunyai titik potong dengan sumbu x. Kurva dapat berada di atas sumbu x atau berada di bawah sumbu x.
Jika nilai koefisien di depan x2 positif (a > 0) maka kuva akan terbuka ke atas dan berada di atas sumbu x. Kondisi saat kurva berada di atas sumbu x dan terbuka ke atas disebut definit positif. Nilai fungsi kuadrat f(x) dengan definit positif akan selalu positif untuk semua nilai x.

Sementara untuk nilai koefisien di depan x2 negatif (a < 0) akan menghasikan kurva terbuka ke bawah dan berada di bawah sumbu x. Kondisi saat kurva berada di bawah sumbu x dan terbuka ke bawah disebut definit negatif. Nilai fungsi kuadrat f(x) dengan definit negatif akan selalu negatif untuk semua nilai x.
2) Diskriminan Positif (D ≥ 0)
Nilai diskriminan positif (D ≥ 0) memberikan informasi bahwa akar-akar persamaan kuadrat adalah bilangan real.
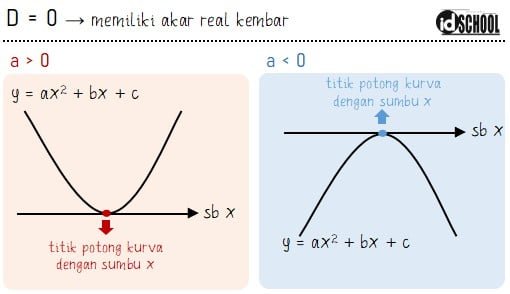
Persamaan kuadrat dengan nilai D = b2 ‒ 4ac = 0 memiliki satu akar real yang sering disebut memiliki solusi akar-akar real kembar. Jika digambarkan dalam sebuah kurva maka hasilnya adalah kurva yang memotong sumbu x pada satu titik. Kurva yang dihasilkan dapat terbuka ke atas (a > 0) atau terbuka ke bawah (a < 0).
Sebagai contoh pada persamaan kuadrat x2 ‒ 3x + 9 = 0 memiliki nilai D = b2 ‒ 4ac = (‒3)2 ‒ 4(1)(9) = 0. Dari hasil hitung diperoleh nilai diskriminan D = 0 yang menunjukkan bahwa persamaan kuadrat x2 ‒ 3x + 9 = 0 memiliki satu akar kembar. Untuk lebih jelasnya perhatikan hasil dari penyelesaian akar-akar dari persamaan kuadrat x2 ‒ 3x + 9 = 0 berikut.
x2 ‒ 3x + 9 = 0
(x ‒ 3)(x ‒ 3) = 0
x ‒ 3 = 0 atau x ‒ 3 = 0
x = 3 atau x = 3
Diperoleh dua akar real kembar yaitu x = 3
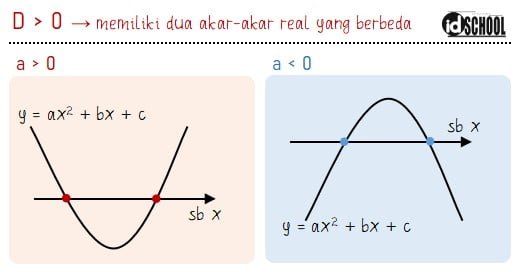
Persamaan kuadrat dengan nilai D > 0 atau b2 ‒ 4ac > 0 memiliki dua akar real yang berbeda nilainya. Jika digambarkan dalam sebuah kurva maka hasilnya adalah kurva yang memotong sumbu x pada dua titik. Kurva yang dihasilkan dapat terbuka ke atas (a > 0) atau terbuka ke bawah (a < 0).
Sebagai contoh pada persamaan kuadrat x2 ‒ x ‒ 6 = 0 memiliki nilai D = b2 ‒ 4ac = (‒1)2 ‒ 4(1)(‒6) = 1 + 24 = 25. Nilai diskriminan D = 25 > 0 menunjukkan bahwa persamaan kuadrat x2 ‒ x ‒ 6 = 0 memiliki dua akar real yang berbeda. Untuk lebih jelasnya perhatikan hasil dari penyelesaian akar-akar dari persamaan kuadrat x2 ‒ x ‒ 6 = 0 berikut.
x2 ‒ x ‒ 6 = 0
(x + 2)(x ‒ 3) = 0
x + 2 = 0 atau x ‒ 3 = 0
x = ‒2 atau x = 3, diperoleh dua akar real berbeda
Baca Juga: Cara Menentukan HP (Himpunan Penyelesaian) dari Pertidaksamaan Kuadrat
Contoh Penggunaan Syarat Agar Persamaan Kuadrat Mempunyai Dua Akar Real
Dari bahasan di atas dapat disimpulkan bahwa syarat agar persamaan kuadrat mempunyai dua akar real adalah mempunyai nilai D > 0. Untuk lebih jelasnya, penyelesaian soal berikut dapat menjadi contoh bagaimana penggunaan syarat agar persamaan kuadrat mempunyai dua akar real.
Soal:
Tentukan nilai p agar persamaan kuadrat 2x2 + 7x ‒ p = 0 memiliki dua buah akar real yang berbeda!
Penyelesaian:
Dari persamaan kuaadrat yang diberikan pada soal dapat diketahui bahwa a = 2, b = 7 dan c = ‒p. Syarat agar persamaan kuadrat mempunyai dua akar real ketika memenuhi syarat nilai diskriminan positif (D > 0) atau b2 ‒ 4ac > 0.
Substitusi nilai a, b, dan c ke syarat agar persamaan kuadrat mempunyai dua akar real sehingga diperoleh pertidaksamaan seperti berikut.
b2 ‒ 4ac > 0
(7)2 ‒ 4(2)(‒p) > 0
49 + 8p > 0
8p > 49
p > 49/8
p > 61/8
Baca Juga: Cara Menentukan Fungsi Kuadrat yang Sesuai dengan Suatu Kurva
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idshcool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana cara penggunaan syarat agar persamaan kuadrat mempunyai dua akar real berbeda. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Syarat Agar Persamaan Kuadrat Mempunyai Dua Akar Real

Pembahasan:
Agar persamaan kuadrat mempunyai dua akar real dipenuhi saat nilai diskriminan positif (D > 0) atau b2 ‒ 4ac > 0. Di mana b adalah koefisien x, a adalah koefisien x2, dan c adalah konstanta. Dari persamaan kuadrat (m ‒ 5)x2 ‒ 4mx + m ‒ 2 = 0 diperoleh nilai a = m ‒ 5, b = ‒4m, dan c = m ‒ 2.
Syarat persamaan kuadrat memilki dua akar real: b2 ‒ 4ac > 0
(‒4m)2 ‒ 4(m ‒ 5)(m ‒ 2) > 0
16m2 ‒ 4(m2 ‒ 7m + 10) > 0
16m2 ‒ 4m2 + 28m ‒ 40 > 0
12m2 + 28m ‒ 40 > 0
3m2 + 7m ‒ 10 > 0
Diperoleh pertidaksamaan 3m2 + 7m ‒ 10 > 0, untuk mengetahui nilai m yang memenuhi perlu mengetahui faktor dari harga nol untuk pertidaksmaan tersebut.
Harga nol: 3m2 + 7m ‒ 10 = 0
3m2 + 3m ‒ 10m ‒ 10 = 0
3m(m + 1) ‒ 10(m + 1) = 0
(3m ‒ 10)(m + 1) = 0
m = 10/3 atau m = ‒1
Selanjutnya adalah menentukan daerah yang memenuhi nilai m pada pertidaksamaan 3m2 + 7m ‒ 10 > 0. Daerah yang memenuhi nilai m adalah daerah yang menghasilkan nilai positif seperti yang ditunjukkan pada daerah berikut.
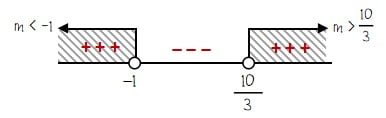
Jadi, batas-batas nilai m yang memenuhi adalah m > 10/3 atau m < ‒1.
Jawaban: D
Contoh 2 – Soal Syarat Persamaan Kuadrat Tidak Mempunyai Akar Real
Jika persamaan kuadrat x2 + (p + 1)x + (2 ‒ p) = 0 memiliki akar-akar yang tidak real, nilai p yang memenuhi persamaan tersebut adalah ….
A. ‒1 < p < 7
B. ‒7 < p < 1
C. ‒7 ≤ p ≤ 1
D. p ≤ ‒1 atau p ≥ 7
E. p < ‒7 atau p > 7
Pembahasan:
Akar-akar yang tidak real dipenuhi ketika nilai diskriminan negatif (D < 0) atau b2 ‒ 4ac < 0. Di mana nilai a, b, dan c yang sesuai untuk persamaan kuadrat a = 1, b = p + 1, dan c = 2 ‒ p. Nilai p yang memenuhi agar persamaan kuadrat memiliki akar-akar tidak real dapat diperoleh seperti cara berikut.

Jadi, nilai p yang memenuhi persamaan tersebut adalah ‒7 < p < 1.
Jawaban: B
Demikianlah tadi ulasan bagaimana syarat agar persamaan kuadrat mempunyai dua akar real. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Persamaan Parabola Hasil Irisan Kerucut
