Aplikasi integral luas daerah berguna untuk menghitung luas bangun datar yang tidak beraturan. Contohnya bangun datar yang dibatasi oleh kurva. Luas daerahnya sama dengan hampiran jumlah luas irisan-irisan kecil segi empat.
Misalnya pada daerah di bawah kurva f(x) = 1 + √x dari x = 0 sampai x = 4. Luas daerah sama dengan hampiran jumlah irisan-irisan kecil seperti yang ditunjukkan pada gambar berikut.

Saat lebar irisan dibuat sangat kecil mendekati nol. Opersi hitung jumlah A = Ʃ Δxi · f(x) menjadi A = a∫b f(x) dx. Detail penjelasan aplikasi integral luas daerah ada di bawah.
Daftar isi:
Baca Juga: Aplikasi Turunan untuk Mencari Luas Maksimum/Minimum Suatu Daerah
Aplikasi Integral Luas Daerah
Luas daerah diperoleh dari jumlah hampiran irisan-irisan kecil berbentuk segi empat. Bentuk irisan dapat dilakukan secara vertikal atau horizontal.
1) Betuk Irisan Vertikal
Saat mengiris daerah secara vertikal. Panjang daerah sama dengan tinggi kurva f(x) dan lebar daerah sama dengan lebar irisan. Sehingga luas irisan sama dengan lebar irisan dikali tinggi kurva, luas irisan = f(x) · Δx.
Untuk daerah yang dibatasi dua kurva, misalkan f(x) dan g(x), tinggi daerah sama dengan selisih dua kurva tersebut. Sehingga luas daerah sama dengan Δx · [f(x) − g(x)]
Jumlah luas semua irisan sama dengan luas daerah. Saat lebar irisan dihampiri sangat kecil mendekati nol. Luasnya daerah menjadi fungsi integral. Batas integral biasanya merupakan titik potong dari kurva.
Contohnya:
Tentukan luas yang dibatasi oleh y = x2 dan y = −x + 2!
Jawab:
Kurva y = x2 dan garis y = −x + 2 berpotongan saat memenuhi persamaan x2 = −x + 2. Perpotongan kedua kurva ini akan menjadi batas pengintegralan.
Menentukan titik potong kurva:
x2 = −x + 2
x2 + x − 2 = 0
Hasil pemfaktoran: (x + 2)(x − 1) = 0
Diperoleh dua nilai x yaitu x = −2 dan x = 1. Sehingga titik potong kedua kurva adalah titik (−2, 4) dan (1, 2).
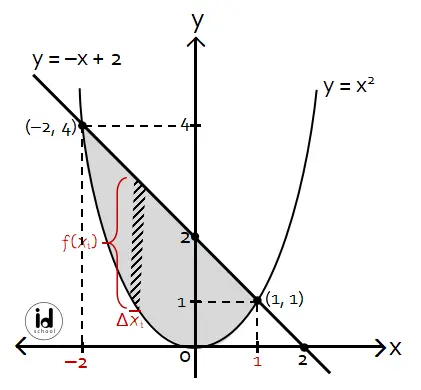
Menghitung luas daerah:
Luas = Ʃ f(xi) · Δxi
= –2∫1 [(–x + 2) – x2] dx
Sehingga,
Luas = [–1/2(1)2 + 2(1) – 1/3(1)3] – [–1/2(–2)2 + 2(–2) – 1/3(–2)3]
= 7/6 – (–20/6)
= 27/6 = 4,5 satuan luas
2) Betuk Irisan Horizontal
Saat mengiris daerah secara horizontal. Panjang daerah sama dengan tinggi kurva f(y) dan lebar daerah sama dengan lebar irisan. Sehingga luas irisan sama dengan lebar irisan dikali tinggi kurva, luas irisan = f(y) · Δy.
Contohnya:
Tentukan luas daerah di antara kurva x = y2 − 2y dan x − y − 4 = 0!
Jawab:
Titik potong antara kedua kurva terjadi saat nilai y memenuhi persamaan y2 − 2y = y + 4. Nilai y yang memenuhi diperoleh dengan menyelesaikan persamaan tersebut.
Menentukan titik potong kurva:
y2 − 2y = y + 4
y2 − 3y − 4 = 0
Hasil pemfaktoran: (y − 4)(y + 1) = 0
Diperoleh dua nilai y yang memenuhi yaitu y = 4 dan y = −1. Dua nilai y ini menjadi batas integral saat menghitung luas daerah di antara kurva x = y2 − 2y dan x − y − 4 = 0.
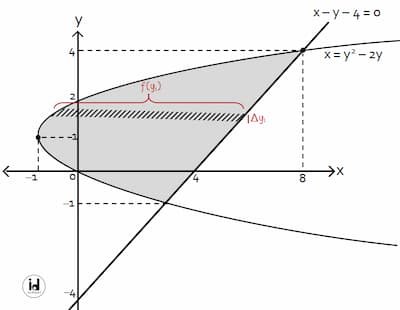
Menghitung luas daerahnya:
Luas = Ʃ f(yi) · Δyi
= –1∫4 y + 4 − (y2 − 2y) dy
= –1∫4 4 + 3y − y2 dy
Sehingga,
= (4 · 4 + 3/2 · 42 − 1/3 · 43) − (4(−1) + 3/2(−1)2 − 1/3(−1)3)
= (16 + 24 − 211/3) − (−4 + 3/2 + 1/3) = 205/6 sat. luas
Jadi, luas daerah di antara kurva x = y2 − 2y dan x − y − 4 = 0 adalah 205/6 satuan luas.
Baca Juga: Cara Menghitung Volume Benda Putar
Contoh Soal dan Pembahasan
Lebih banyak pembahasan soal aplikasi integral luas daerah ada di bawah.
Contoh 1
Luas daerah yang dibatasi kurva y = x2 dan garis y = 5x – 4 adalah … satuan luas.
A. 41/2
B. 51/2
C. 7
D. 9
E. 91/2
Pembahasan:
Sebelum menghitung luas, perlu untuk mengetahui batas integralnya. Batas integral yang digunakan merupakan titik potong antara kurva dan garis.
Menentukan batas intergal:
x2 = 5x – 4
x2 – 5x + 4 = 0
Hasil pemfaktoran: (x – 4)(x – 1) = 0
Diperoleh dua nilai x yaitu x = 1 dan x = 4. Kedua nilai x akan menjadi batas integral saat menghitung luasnya.
Menghitung luas daerah:
Luas = 1∫4 (5x – 4) – x2 dx
= 1∫4 5x – 4 – x2 dx
= [5/2x2 – 4x – 1/3 x3]14
Sehingga,
Luas = [5/2(4)2 – 4(4) – 1/3(4)3] – [5/2(1)2 – 4(1) – 1/3(1)3]
= [40 – 16 – 64/3] – [5/2 – 4 – 1/3]
= 28 – 63/3 – 5/2 = 41/2 satuan luas.
CARA CEPAT:
Dari persmaaan kurva dan garis 5x – 4 = x2. Maka x2 – 5x + 4 = 0.
Nilai diskriminan dari persamaan kuadrat x2 – 5x + 4 = 0 adalah D = 25 – 4(1)(4) = 25 – 16 = 9.
Sehingga,
Jadi, luas daerah yang dibatasi kurva y = x2 dan garis y = 5x – 4 adalah 41/2 satuan luas.
Jawaban: A
Contoh 2
Luas daerah yang dibatasi oleh kurva y = 1 – x2, sumbu y, sumbu x, dan garis x = 3 adalah … satuan luas.
A. 251/3
B. 24
C. 71/3
D. 6
E. 42/3
Pembahasan:
Gambar daerah yang di antara kurva y = 1 – x2, sumbu y, sumbu x, dan garis x = 3 ditunjukkan seperti berikut.
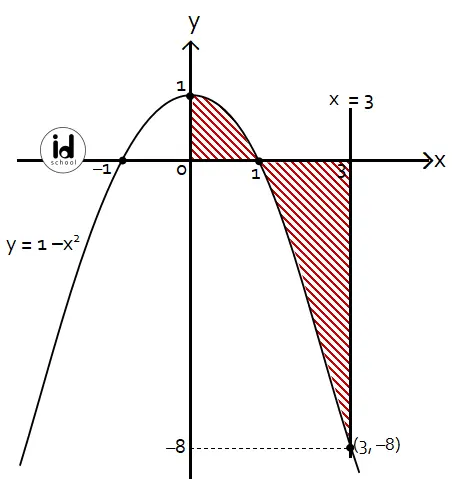
Menghitung luas daerah:
Luas = 0∫1 1 – x2 dx – 1∫3 1 – x2 dx
Luas = [x – 1/3x3]01 – [x – 1/3x3]13
Sehingga,
Luas = [1 – 1/3(1)3] – [(3 – 2/3(3)3) – (1 – 1/3(1)3)]
= 2 × [1 – 1/3(1)3] – [3 – 1/3(3)3]
= 4/3 – (–6) = 11/3 + 6 = 71/3 sat. luas
Jadi, luas daerah yang dibatasi oleh kurva y = 1 – x2, sumbu y, sumbu x, dan garis x = 3 adalah 71/3 satuan luas.
Jawaban: C
Contoh 3
Perhatikan gambar berikut!

Luas daerah di antara kurva adalah ….
(A) 2
Pembahasan:
Aplikasi integral luas daerah di antara kurva untuk soal ini perlu dihitung secara terpisah menjadi dua. Pertama untuk daerah yang dibatasi oleh kurva y = √x dan sumbu x. Kedua untuk daerah yang dibatasi garis y = –x + 6.

Menghitung luas daerah:
Luas = 0∫4 √x dx + 4∫6 6 – x dx
Luas = [2/3√x3]04 + [6x – 1/2x2]46
Sehingga,
Luas = [2/3√43 – 2/3√03] + [(6 · 6 – 1/2 · 62) – (6 · 4 – 1/2 · 42)]
= [2/3√64 ] + [18 – 16]
= 16/3 + 2 = 51/3 + 2 = 71/3 satuan luas
Jadi, luas di antara kurva y = √x dan y = –x + 6 adalah 71/3 satuan luas.
Sekian ulasan aplikasi integral luas daerah. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
