Aturan sinus menyatakan hubungan antara perbandingan panjang sisi dengan sudut yang bersesuaian terhadap fungsi sinus. Persamaannya meliputi tiga perbandingan yang menyatakan hubungan antara panjang sisi-sisi dengan sudut-susut yang berhadapan. Penggunaan aturan sinus sangat dibutuhkan untuk menentukan panjang sisi atau besar sudut pada segitiga sembarang. Aturan ini juga dapat digunakan untuk mengetahui luas segitiga sembarang.
Pada segitiga siku – siku, fungsi sinus menyatakan hubungan sisi depan dan sisi miring. Sehingga, dengan mudah fungsi sinus dapat digunakan untuk menentukan sisi segitiga lain yang belum diketahui. Pada segitiga sembarang, sisi miring segitiga tidak dapat ditentukan, begitu juga dengan sisi depan dan samping segitiga sembarang. Dengan demikian, sisi segitiga yang lain juga tidak dapat langsung dicari menggunakan persamaan fungsi sinus, tetapi dapat menggunakan aturan sinus.
Bagaiman bentuk aturan sinus? Bagaimana contoh penggunannya? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Pengantar Materi Aturan Sinus
Aturan sinus merupakan persamaan yang menyatakan hubungan tiga sudut dan tiga sisi yang terdapat pada segitiga sembarang. Tujuan dari penggunaan aturan sinus adalah untuk mengetahui panjang sisi segitiga yang terdapat pada segitiga sembarang. Atau dapat juga digunakan untuk mengetahui besar sudut segitiga yang belum diketahui.
Sebelumnya, sobat idschool sepertinya perlu tahu dari mana persamaan sinus diperoleh. Simak cara mendapatkan persamaan aturan sinus yang akan diberikan di bawah.
Perhatikan gambar segitiga ABC di bawah!

Pada ∆ACR dapat diperoleh sebuah persamaan seperti berikut.

Pada ∆BCR dapat diperoleh sebuah persamaan seperti berikut.
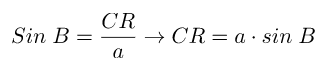
Berdasarkan dua persamaan di atas, dapat disimpulkan persamaan berikut.
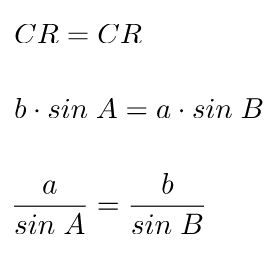
Diperoleh sebuah aturan sinus yang menyatakan hubungan panjang sisi dan sudut pada suatu segitiga. Dengan cara yang serupa akan diperoleh persamaan aturan sinus seperti yang diberikan pada persamaan di bawah.
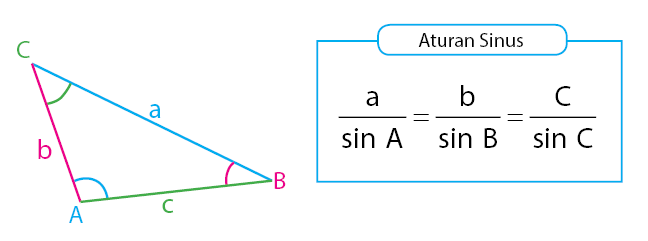
Baca Juga: Cara Menghitung Luas Segitiga Sembarang
Fungsi aturan sinus di atas dapat digunakan untuk menentukan panjang sisi segitiga yang belum diketahui. Selain itu, juga dapat digunakan untuk mencari besar sudut segitiga yang belum diketahui.
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Menentukan Panjang Salah Satu Sisi Segitiga
Suatu segitiga ABC memiliki panjang AC = 8 cm. Jika besar ∠BAC = 45o dan ∠ABC = 60o maka panjang BC = … cm.
A. 8
B. 7
C. 8√3/√2
D. 4√2
E. 8√6/3
Pembahasan:
Berdasarkan informasi yang diberikan pada soal, dapat diperoleh informasi seperti berikut ini.
Panjang BC dapat dicari menggunakan aturan sinus seperti yang dilakukan pada proses pengerjaan berikut.
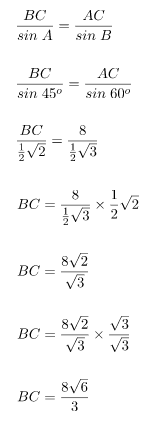
Jadi, panjang BC = 8√6/3 cm.
Jawaban: E
Contoh 2 – Menentukan Panjang Salah Satu Sisi Segitiga
Diketahui segitiga ABC dengan besar sudut A adalah 60o, sudut B adalah 45o, dan panjang sisi AC sama dengan 10 cm. Panjang BC pada segitiga ABC tersebut adalah ….
A. 8√3 cm
B. 6√6 cm
C. 6√5 cm
D. 5√6 cm
E. 5√3 cm
Pembahasan:
Cara menghitung panjang BC pada segitiga ABC dapat dilakukan seperti cara berikut.
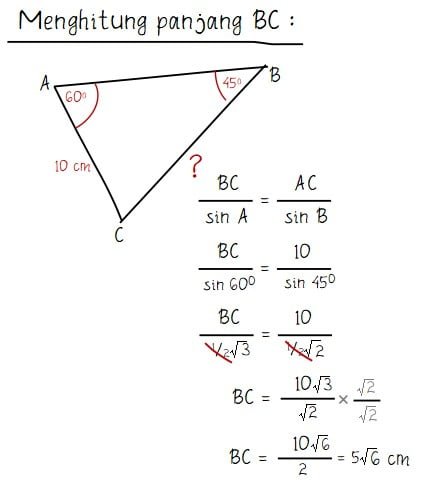
Jasi, panjang BC pada segitiga ABC sama dengan 5√6 cm.
Jawaban: D
Baca Juga: Aturan Cosinus (Materi dan Contoh Soal + Pembahasan)
Contoh 3 – Luas Segitiga
Diketahui suatu taman di tengah kota berbentuk segitiga sembarang. Jika sudut apit sebesar 60o dan dua sisi yang mengapitnya masing-masing panjangnya 18 meter dan 16 meter, maka luas taman tersebut adalah ….
A. 72 m2
B. 72√2 m2
C. 72√3 m2
D. 144 m2
E. √106/4 m2
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal maka dapat diperoleh sebuah segitiga dengan dua panjang sisi dan sebuah besar sudut yang sudah diketahui.

Menghitung luas taman:
L = 1/2 × alas × tinggi
= 1/2 × 18 × 16 × sin 60o
= 1/2 × 18 × 16 × 1/2√3
= 72√3 m2
Jadi, luas taman tersebut adalah 72√3 m2.
Jawaban: C
Sekian pembahasan aturan sinus yang meliputi bentuk tiga perbandingan beserta contoh soal dan pembahasannya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Cara Menyelesaikan Persamaan Trigonometri
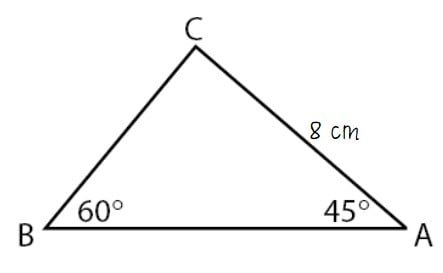

Terima kasih, mohon soal dan pembahasan diperbaiki. Di soal kurang diketahui sudut ABC = 60 derajat, dan di pembahasan panjang AC adalah 10 cm sedangkan di soal 8 cm
terima kasih atas soal yang dierikan, tapi bisakah soal itu diperbaiki? di soal tidak ada yang menyebutkan bahwa sudut ABC adalah 60 derajat