Simbol fungsi turunan pertama dari f(x) dinyatakan dalam f’(x) yang dibaca f aksen x. Turunan suatu fungsi f(x) dapat diperoleh melalui definisi turunan yang akan menghasilkan fungsi baru f ’ (x). Sayangnya, cara untuk mendapatkan turunan suatu fungsi dengan definisi turunan tidak praktis untuk dilakukan. Sehingga dibutuhkan cara lain untuk menentukan turunan suatu fungsi. Cara menentukan turunan suatu fungsi f(x) yang lebih mudah dapat dilakukan melalui aturan turunan.
Aturan turunan merupakan teorema fungsi turunan yang dapat digunakan untuk menentukan apa hasil turunan dari suatu fungsi. Bagaimana sajakah aturan turunan untuk menentukan hasil turunan suatu fungsi? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Pencarian Turunan Fungsi dengan Definisi
- Teorema dalam Aturan Turunan
- Contoh Soal dan Pembahasan
- Contoh 2 – Penggunaan Aturan Turunan untuk Menyelesaikan Soal Turunan
Pencarian Turunan Fungsi dengan Definisi

Sebelum ke bahasan aturan turunan, sebaiknya ingat kembali bagaimana definisi turunan. Keluaran fungsi turunan berupa f’(x) merupakan fungsi baru yang berbeda dari f(x) setelah mengalami operasi sesuai definisi turunan. Persamaa dalam definisi turunan merupakan nilai limit dari hasil bagi selisih untuk suatu nilai.
Berikut ini akan ditunjukkan bagaimana hasil turunan suatu fungsi yang dapat diperoleh melalui definisi turunan.
- Akan dicari nilai turunan fungsi f(x) = 3x – 5 menggunakan definisi turunan.
- Diketahui:
f(x) = 3x + 5
f(x+h) = 3(x+h) + 5
- Mencari turunan pertama f(x) = 3x – 5 dengan definisi turunan:
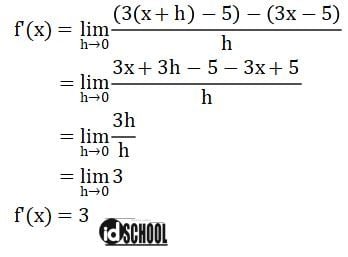
Jadi, fungsi turunan pertama dari f(x) = 3x – 5 adalah f’(x) = 3.
Tentu saja cara mencari turunan suatu fungsi seperti cara di atas akan sangat merepotkan dan memakan banyak waktu. Sehingga perlu cara lain agar dapat memperoleh turunan suatu fungsi dengan lebih cepat dan praktis. Cara tersebut termuat dalam aturan turunan yang dapat digunakan untuk mendapatkan turunan suatu fungsi dengan lebih mudah.
Baca Juga: Pengerian Turunan
Teorema dalam Aturan Turunan
Aturan turunan yang tersedia meliputi aturan konstanta, fungsi identitas, aturan pangkat, dan kelipatan konstanta. Selain itu terdapat juga aturan turuan yang memuat aturan jumlah, selisih, hasil kali dua fungsi, hasil bagi fungsi, dan aturan rantai.
Aturan turunan dapat dibuktikan kebenarannya melalui definsi turunan. Sehingga penggunaan aturan tersebut akan menhasilkan hasil yang sama dengan hasil pencarian turunan melalui definisi.
Rumus-rumus dalam aturan turunan diperoleh dengan mengambil persamaan umum. Hasil yang diperoleh kemudian dapat digunakan untuk menyelesaikan persamaan yang lebih khusus.
Sebagi contoh pada aturan konstanta: Jika f(x) = k dengan k adalah suatu konstanta maka f’(x) = 0.
Turunan dari f(x) = k (k adalah konstanta):
f(x) = k
f’(x) = limh→0 k – k/h
= limh→0 0/h
= limh→0 0
f’(x) = 0
Dari hasil di atas dapat disimpulkan bahwa turunan fungsi untuk semua konstanta adalah nol. Selanjutnya, sobat idschool dapat menggunakan aturan konstanta tersebut untuk mendapatkan turunan dari suatu konstanta.
Contoh:
- f(x) = 5 → f’(x) = 0
- g(x) = 125 → g’(x) = 0
- p(t) = –2 → p’(t) = 0
Berikutnya, pada fungsi identitas: Jika f(x) = x dengan n bilangan bulat positif maka f’(x) = 1.
Diketahui:
f(x) = x
f(x + h) = x + h
Mencari turunan pertama f(x) = x dengan definisi turunan:

Dua pemisalan di atas merupakan beberapa contoh cara mendapatkan rumus umum dalam aturan turunan. Rumus-rumus umum dalam aturan pencarian turunan akan sangat membantu untuk menemukan turunan suatu fungsi yang cukup rumit.
Daftar rumus aturan turunan lainnya dapat dilihat seperti tabel berikut.

Aturan dalam pencarian turunan tersebut dapat dibuktikan melalui definisi turunan. Selanjutnya, sobat idschool hanya perlu menggunakan aturan-aturan tersebut untuk mencari turunan suatu fungsi. Cara pencarian turunan tentu akan lebih mudah dan cepat dibanding menggunakan definisi turunan secara langsung.
Baca Juga: Turunan Fungsi Trigonometri
Contoh Soal dan Pembahasan
Beberapa contoh soal beserta pembahasannya di bawah akan menunjukkan bagaimana penerapan aturan turunan untuk mencari turunan suatu fungsi. Sobat idschool dapat mengasah kemampuan dalam mencari turunan suatu fungsi melalui beberapa contoh soal dan pembahasannya di bawah.
Contoh 1 – Soal Mencari Turunan Suatu Fungsi
Turunan pertama dari fungsi f(x) = sin23x adalah ….
A. 2 sin 3x
B. sin 6x
C. 2 cos 3x
D. 3 sin 6x
E. –3 sin 6x
Pembahasan:
Langkah pertama yang perlu dilakukan adalah memisalkan fungsi dalam variabel u seperti cara berikut.
- Misalkan:
u = sin 3x → Dx(u) = 3 cos 3x
f(x) = u2 → Du(f(x)) = 2u
Mencari turunan pertama dari fungsi f(x) dengan aturan turunan – aturan rantai: Dx[f(x)] = Du[f(x)] · Dx[u]
f(x) = sin23x
f'(x) = Dx[f(x)]
Dx[f(x)] = 3 cos 3x · 2u
Dx[f(x)]= 3 cos 3x · 2 sin 3x
= 3 (2 · sin 3x · cos 3x)
= 3 sin 6x
Jadi, turunan pertama dari fungsi f(x) = sin23x adalah f'(x) = 3 sin 6x.
Jawaban: D
Contoh 2 – Penggunaan Aturan Turunan untuk Menyelesaikan Soal Turunan
Jika f’(x) adalah turunan dari f(x) maka turunan dari f(ax + b) adalah ….
A. f’(ax + b)
B. a · f’(ax) + b
C. a · f’(x)
D. a · f’(ax + b)
E. a · f’(x) + b
Pembahasan:
Dari soal dapat diperoleh informasi bahwa,
- g(x) = ax + b
- Dxg(x) = a
Dengan aturan turunan – aturan rantai akan dicari turunan pertama dari dari f(ax + b).
f’(ax + b) = f’(g(x))
f’(ax + b) = Dx[f(ax + b)] · Dx(g(x))
= f’(ax + b) · a
= a · f’(ax + b)
Jadi, jika f’(x) adalah turunan dari f(x) maka turunan dari f(ax + b) adalah a · f’(ax + b).
Jawaban: D
Demikianlah tadi ulasan teorema atau aturan turunan untuk mempermudah cara mencari turunan suatu fungsi. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
