Secara umum fungsi eksponen adalah persamaan yang memuat bilangan berpangkat. Ada dua macam bentuk grafik fungsi eksponen untuk bentuk umum dasar adalah y = ax dengan a = bilangan real dan x = variabel pangkat. Dua bentuk grafik fungsi eksponen dibedakan berdasarkan nilai a (basis) dalam fungsi eksponen yaitu grafik eksponensial monoton naik dan monoton turun.
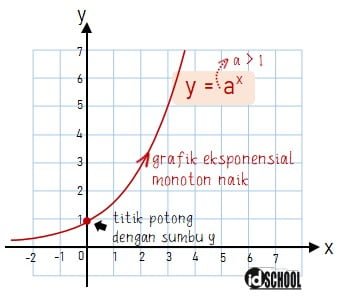
Untuk fungsi eksponen y = ax dengan a > 1 maka grafik eksponensial akan berupa kurva monoton naik dan memotong sumbu y di titik (0, 1). Bentuk umum grafik eksponensial monoton naik sesuai dengan gambar berikut.
Baca Juga: Cara Menggambat Grafik Fungsi Eksponen dalam 4 Langkah
Untuk fungsi eksponen y = ax dengan a berada pada selang 0 < a > 1 maka grafik eksponensial berupa monoton turun dan memotong sumbu y di titik (0, 1). Bentuk umum grafik eksponensial monoton turun sesuai dengan gambar berikut.

Karakteristik gfrafik fungsi eksponen y = ax selalu memiliki titik memotong sumbu y di titik (0, 1). Kondisi ini terjadi karena berapun nilai basis bilangan eksponen yang dipangkatkan nol akan sama dengan 1. Sementara untuk perpotongan dengan sumbu x tidak ada dan grafik fungsi eksponen memiliki asymtot horizontal (asimtot dasar).
Fungsi eksponen y = ax selalu menghasilkan nilai y positif untuk berapapun nilai x, sehingga grafik eksponensial y = ax merupakan definit positif.
Bentuk fungsi eksponen dapat berupa bentuk lain seperti penambahan konstanta, misalnya y = ax + c. Bentuk fungsi eksponen juga dapat memuat perkalian dengan suatu bilangan seperti pada persamaan y = k⋅ax.
Bagaimana pengaruh penambahan konstanta pada fungsi eksponen terhadap pada bentuk grafik fungsi eksponen yang dihasilkan? Bagaimana pengaruh perkalian fungsi eksponen dengan suatu bilangan terhadap bentuk grafik fungsi eksponen yang dihasilkan? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Baca Juga: Cara Menggambar Grafik Fungsi Kuadrat
Fungsi Eksponen
Eksponen disebut juga degan bilangan berpangkat yaitu perkalian suatu bilangan yang sama sebanyak bilangan pangkatnya. Misalkan fungsi y adalah perkalian bilangan 2 sebanyak lima kali (y = 2 × 2 × 2 × 2 × 2) memiliki bentuk fungsi eksponen y = 25. Sehingga dapat dikatakan bahwa fungsi eksponen adalah persamaan yang memuat bentuk bilangan berpangkat.
Bentuk umum ekponen adalah an (dibaca: a pangkat n) di mana a disebut basis yaitu bilangan yang dikalikan sementara n adalah bilangan pangkatnya.
Fungsi eksponen memiliki beberapa sifat yang dapat digunakan dalam melakukan operasi hitung. Beberapa sifat fungsi eksponen terdapat seperti sifat-sifat berikut.
- Bilangan berpangkat nol: a0 = 1
- Penjumlahan: am + n = am ⋅ an
- Pengurangan: am ‒ n = am : an
- Perkalian: am × n = (am)n
- Perkalian berpangkat: (a × b) m = am ⋅ bn
- Pembagian berpangkat: (a : b) n = an : bn
- Pangkat negatif: a‒n = 1/a^n
- Pangkat pecahan: a¾ = 4√a3
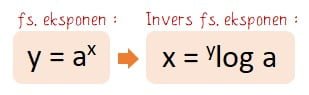
Invers dari fungsi eksponen adalah fungsi logaritma, di mana invers fungsi eksponen y = ax adalah fungsi logaritma x = ylog a.
Baca Juga: Persamaan dan Pertidaksamaan Eksponen
Berbagai Bentuk Grafik Fungsi Eksponen
Grafi fungsi eksponen merupakan fungsi kontinu yaitu grafik fungsi yang kurvanya tidak terputus atau terdefinisi di setiap titik. Sehingga grafik fungsi ekponensial berupa kurva lengkung yang selalu menanjak atau menurun. Sebuah kurva yang nilainya selalu naik atau selalu turun disebut dengan grafik monoton.
Bentuk grafik fungsi eksponen secara umum dibedakan menjadi dua berdasarkan nilai a dari fungsi eksponen y = ax. Kedua bentuk grafik fungsi eksponen berdasarkan nilai a yaitu grafik eksponensial menanjak (kurva monoton naik) dan grafik eksponensial menurun (kurva monoton turun).
- Kurva monoton naik: bentuk kurva semakin menaik karena nilai/data semakin besar
- Kurva monoton turun: bentuk kurva semakin menurun karena nilai/data semakin kecil
Penambahan atau perkalian suatu konstanta pada bentuk fungsi dasar eksponen y = ax dapat membuat bentuk grafik fungsi kuadrat. Bagaimana perubahan bentuk dasar grafik fungsi eksponen karena penambahan atau perkalian konstanta dapat dilihat pada masing-masing berikut.
1) Pengaruh penambahan/pengurangan konstanta: y = ax + c
Fungsi eksponen dasar dengan penambahan atau pengurangan konstata c memilki bentuk umum y = ax + c. Penambahan konstanta c akan menggeser bentuk dasar grafik fungsi eksponen ke atas sebanyak c satuan. Sementara pengurangan konstanta c akan menggeser bentuk dasar grafik fungsi eksponen ke bawah sebanyak c satuan.
Misalnya pada grafik fungsi eksponen y = 2x memiliki titik potong dengan sumbu y di titik (0, 1). Penambahan konstanta c = 1 akan membuat grafik fungsi eksponen berseser ke atas sebanyak 1 satuan. Pengurangan konstanta c = 1 akan membuat grafik fungsi eksponen berseser ke bawah sebanyak 1 satuan.
Perubahan bentuk dasar grafik fungsi eksponen karena penambahan dan pengurangan suatu konstanta ditunjukkan seperti gambar di bawah.

2) Pegaruh perkalian konstata: y = k ⋅ ax
Fungsi eksponen bentuk dasar y = ax dapat dikalikan dengan konstanta k sehingga memiliki bentuk umum y = k ⋅ ax. Perubahan bentuk grafik fungsi kuadrat dari bentuk dasarnya bergantung dari nilai konstantan k pengalinya.
Untuk nilai k = ‒1 akan merubah bentuk dasar grafik fungsi eksponen menjadi grafik hasil pencerminannya. Untuk nilai k pecahan akan membuat grafik fungsi eksponen monoton naik menjadi kurva monoton turun, begitu juga untuk sebaliknya. Sementara untuk nilai k berupa bilangan bulat positif akan merubah tingkat kelengkungan grafik fungsi eksponen.

Baca Juga: Interval Fungsi Naik dan Fungsi Turun
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Bentuk Grafik Eksponen
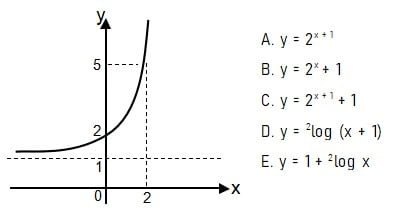
Persamaan grafik fungsi pada gambar berikut adalah ….
Pembahasan:
Beberapa langkah untuk menentukan persamaan dari grafik fungsi eksponen:
1) Mencari titik-titik koordinat yang diketahui.
2) Amati bentuk grafik monoton naik atau monoton turun
3) Bentuk persamaan fungsi eksponen
Dari gambar yang diberikan pada soal dapat diketahui bahwa titik-titik koordinat dari grafik fungsi eksponen adalah (0, 2) dan (2, 5).
Grafik fungsi eksponen pada soal adalah bentuk dasar grafik eksponensial monoton naik yang mengalami pergeseran satu satuan ke atas. Hal ini dapat diketahi dari titik potong sumbu y dengan grafik adalah (0, 2). Sehingga dapat diperoleh persamaan untuk kurva tersebut adalah y = ax + 1.
Untuk menentukan nilai a, substitusi titik (2, 5) pada persamaan seperti yang dilakukan pada cara berikut.
y = ax + 1
5 = a2 + 1
a2 = 5 ‒ 1
a2 = 4 → a = ±2
Diketahui bahwa bentuk grafik fungsi eksponen definit positif dan monoton naik maka nilai a yang memebuhi adalah a = 2. Jadi, persamaan grafik fungsi pada gambar berikut adalah y = 2x + 1.
Jawaban: B
Contoh 2 – Soal Bentuk Grafik Eksponensial

Persamaan grafik fungsi eksponen pada gambar di atas adalah ….
A. f(x) = 3x
B. f(x) = 3x + 1
C. f(x) = 3x ‒ 1
D. f(x) = 3x + 1
E. f(x) = 3x ‒ 1
Pembahasan:
Dari grafik diketahui bahwa bentuk dasar grafik fungsi eksponen monoton naik bergeser satu satuan ke atas. Kesimpulan ini diperoleh dari titik koordinat perpotongan sumbu y dengan kurva adalah (0, 2). Sehingga bentuk umum yang sesuai untuk kurva pada soal adalah y = ax + 1.
Nilai a dapat diperoleh dengan melakukan susbtitusi titik (2, 10) ke persamaan y = ax + 1 seperti carai berikut.
y = ax + 1
10 = a2 + 1
a2 = 10 ‒ 1
a2 = 9 ⇒ a = ±3
Bentuk grafik fungsi eksponen pada soal berupa kurva monoton naik sehingga nilai a yang memenuhi adalah a = 3. Jadi, persamaan grafik fungsi eksponen pada gambar di atas adalah y = 3x + 1.
Jawaban: D
Contoh 3 – Soal Bentuk Grafik Eksponen
Pembahasan:
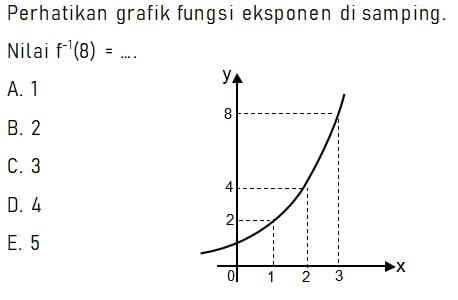
Grafik fungsi eksponen pada soal adalah kurva monoton naik yang melewati titik-titik koordinat (1, 2); (2, 4); dan (3, 8). Dari ketiga titik koordinat yang diketahui dapat diperoleh hubungan bahwa nilai y = 2x. Sehingga persamaan yang sesuai untuk grafik tersebut adalah y = 2x.
Pada soal menanyakan nilai f‒1(8) di mana f‒1(x) adalah fungsi invers dari f(x) = y = 2x. Invers fungsi yang sesuai untuk y = 2x adalah fungsi logaritma x = 2log y.
Diperoleh persamaan f‒1(x) = 2log x, sehingga nilai f‒1(8) = 2log 8 = 3. Jadi, nilai f‒1(8) = 3.
Jawaban: C
Demikianlah tadi ulasan bentuk grafik fungsi eksponen yang terdiri dari beberapa macam. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: 5 Bentuk Persamaan Logaritma yang Sering Muncul pada Soal
