Cara Mencari Persamaan Lingkaran Melalui 3 Titik

Cara mencari persamaan lingkaran melalui 3 titik dilakukan pada lingkaran yang diketahui koordinat tiga titik pada busur lingkaran. Sebuah lingkaran memiliki bentuk umum yang dinyatakan dalam persamaan x² + y² + Ax + By + C = 0. Substitusi 3 titik koordinat yang diketahui ke persamaan lingkaran akan menghasilkan tiga buah persamaan linear dengan 3 varibel.

Ketiga variabel pada persamaan mewakili bilangan-bilangan dalam persamaan lingkaran yang melalui tiga titik tersebut, Nilai variabel dapat ditentukan melalui cara eliminasi, substitusi, atau campuran pada sistem persamaan linear tiga variabel. Dengan mendapatkan nilai ketiga variabel, kemudian dapat diketahui persamaan lingkaran. Contoh gambaran sebuah lingkaran yang memiliki suatu bentuk persamaan lingkaran yang diketahui melalui 3 titik ditunjukkan seperti berikut.

Baca Juga: Persamaan Garis Singgung Lingkaran

Bagaimana cara menentukan persamaan lingkaran yang diketahui melalui tiga titik? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Langkah-Langkah Pengerjaan
• Contoh Soal dan Pembahasan

Langkah-Langkah Pengerjaan

Langkah-langkah menentukan persamaan lingkaran melalui 3 titik:

1. Memisalkan bentuk umum persamaan lingkaran, yaitu x² + y² + ax + by + c = 0
2. Substitusi ketiga titik koordinat pada pemisalan bentuk umum persamaan lingkaran pada langkah pertama
3. Akan diperoleh tiga persamaan dengan tiga variabel
4. Tentukan nilai ketiga variabel (a, b, dan c)
5. Substitusikan nilia variabel yang sudah diperoleh ke bentuk umum persamaan lingkaran
6. Diperoleh bentuk umum persamaan lingkaran

Baca Juga: Kedudukan Antara Dua Lingkaran

Contoh Soal dan Pembahasan

Soal:
Diketahui sebuah lingkaran melalui tiga titik dengan koordinat (3, –1), (5, 3), dan (6, 2). Tentukan persamaan lingkaran, pusat lingkaran, dan jari-jari lingkaran!

Pembahasan:

Bentuk umum persamaan lingkaran: x² + y² + ax + by + c = 0

Substitusi ketiga titik: (3, –1), (5, 3), dan (6, 2) ke bentuk umum persamaan lingkaran di atas sehingga akan diperoleh tiga persamaan dengan tiga variabel.

1. Persamaan (i): substitusi titik (3, –1) pada bentuk umum persamaan lingkaran.
   x² + y² + ax + by + c = 0
   3² + (–1)² + a × 3 + b × (–1) + c = 0
   9 + 1 + 3a – b + c = 0
   3a – b + c = –10

2. Persamaan (ii): substitusi titik (5, 3) pada bentuk umum persamaan lingkaran.
   x² + y² + ax + by + c = 0
   5² + 3² + a × 5 + b × 3 + c = 0
   25 + 9 + 5a + 3b + c = 0
   5a + 3b + c = –34

3. Persamaan (iii): substitusi titik (6, 2) pada bentuk umum persamaan lingkaran.
   x² + y² + ax + by + c = 0
   6² + 2² + 6a + 2b + c = 0
   36 + 4 + 6a + 2b + c = 0
   6a + 2b + c = –40

4. Persamaan (iv): eliminasi c dari persamaan (1) dan (2)

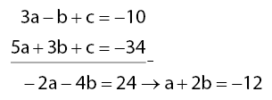
5.  Persamaan (v): eliminasi c dari persamaan (2) dan (3)  

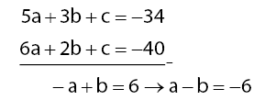
6. Cari nilai b dengan cara eliminasi a dari persamaan (4) dan (5).

7. Substitusi nilai b = –2 pada persamaan (5) untuk mendapatkan nilai a.
   a – b = –6
   a – (–2) = –6
   a + 2 = –6
   a = –6 – 2 = –8

8. Substitusi nilai a = –8 dan b = –2 pada persamaan (i) untuk mendapatkan nilai c.
   3a – b + c = –10
   3(–8) – (–2) + c = –10
   –24 + 2 + c = –10
   –22 + c = –10
   c = –10 + 22 = 12

Diperoleh persamaan lingkaran:
x² + y² + ax + by + c = 0
x² + y² – 8x – 2y + 12 = 0

Pusat lingkaran: koordinat pusat lingkaran: (–¹/₂A, –¹/₂B):
–¹/₂A = –¹/₂ × –8 = 4
–¹/₂B = –¹/₂ × –2 = 1
Jadi, pusat lingkaran adalah P(4, 1)

Jari-jari lingkaran:
r² = (¹/₂A)² + (¹/₂B)² – C
r² = (¹/₂ × –8)² + (¹/₂ × –2)² – 12
r² = (–4)² + (–1)² – 12
r² = 16 + 1 – 12 = 5
r = √5

Sehingga, persamaan lingkaran melalui 3 titik dengan koordinat (3, –1), (5, 3), dan (6, 2) adalah x² + y² – 8x – 2y + 12 = 0. Pusat lingkaran x² + y² – 8x – 2y + 12 = 0 adalah (4, 1) dan jari-jari lingkaran sama dengan r = √5 satuan.

Demikian langkah untuk menentukan persamaan lingkaran melalui 3 titik, terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Sistem Persamaan Linear Tiga Variabel (SPLTV)