Secara umum nilai n pada notasi faktorial memenuhi persamaan n! = n×(n‒1)×(n‒2)×…×3×2×1. Atau, nilai n pada notasi faktorial menyatakan bentuk umum operasi hitung perkalian bilangan berurut dari n yang mengecil sampai 1. Notasi faktorial adalah sebuah operasi hitung yang menyatakan perkalian bilangan asli berurutan. Simbol notasi faktorial adalah tanda seru (!) yang mengikuti sebuah bilangan. Misalkan 3! (dibaca: tiga faktorial) nilainya sama dengan 3! = 3×2×1 = 6.
Nilai n pada notasi faktorial sering juga dinyatakan dalam bentuk persamaan. Di mana pertanyaan sering menanyakan berapa nilai n yang memenuhi persamaan tersebut. Bagaimana cara menentukan nilai n pada notasi faktorial? Bagaimana bentuk soal yang memuat nilai n pada notasi faktorial? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Operasi Hitung dengan Notasi Faktorial
- Notasi Faktorial pada Permutasi (P)
- Notasi Faktorial pada Kombinasi (C)
- Contoh Soal dan Pembahasan
Operasi Hitung dengan Notasi Faktorial
Jika n adalah bilangan asli maka n faktorial (ditulis n!) didefinisikan dengan n! = n × (n–1) × (n–2) × (n–3) × … × 3 × 2 × 1. Dengan kata lain operasi hitung dengan notasi faktorial adalah cara mengalikan bilangan-bilangan asli berurutan dari yang tertinggi sampai ke bilangan asli paling kecil yaitu 1.
Bilangan asli paling besar pada operasi hitung notasi faktorial adalah nilai n pada notasi faktorial. Misalnya pada bilangan dengan notasi faktorial 5! maka bilangan asli paling besar adalah 5. Bentuk nilai n pada notasi faktorial secara umum sesuai dengan persamaan-persamaan berikut.

Notasi Faktorial pada Permutasi (P)
Permutasi adalah aturan mengenai cara menyusun obyek-obyek yang memerhatikan urutan. Operasi hitung permutasi digunakan untuk menentukan banyak cara menyusun k obyek dari n obyek dengan memerhatikan urutan.
Contoh masalah permutasi adalah susunan pengurus kelas atau panitia yang biasanya terdiri dari ketua, wakil, sekretaris, bendahara, dan anggota. Dalam permasalahan ini urutan perlu diperhatikan kedudukan secara urut untuk lima jabatan tersebut memengaruhi susunan. Sebagai contoh lima jabatan yang secara urut diduduki oleh Andi, Beni, Caca, Dea, dan Erni tidak sama dengan susunan Andi, Beni, Erni, Dea, dan Caca. Dua susunan tersebut dipandang berbeda dalam bahasan permutasi.
Permutasi untuk k unsur atau objek dari n unsur disimbolkan P(n, k) atau nPk (Pkn atau nPk) memenuhi persamaan berikut.
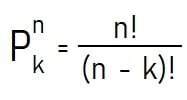
Notasi Faktorial pada Kombinasi (C)
Kombinasi adalah aturan mengenai cara menyusun obyek-obyek yang tanpa memerhatikan urutan. Operasi hitung permutasi digunakan untuk menentukan banyak cara menyusun k obyek dari n obyek tanpa memerhatikan urutan.
Contoh masalah kombinasi terdapat pada cara memilih lima orang dari 10 orang dalam kelas untuk menjadi wakil untuk mengikuti paduan suara. Dalam hal ini memilih Andi, Beni, Caca, Dea, dan Erni menjadi wakil akan sama dengan pemilihan Andi, Beni, Erni, Dea, dan Caca. Dua susunan tersebut dipandang sama dalam bahasan kombinasi.
Kombinasi k unsur dari n unsur yang tersedia disimbolkan C(n, k) atau nCk (Ckn atau nCk) memenuhi bentuk persamaan berikut.
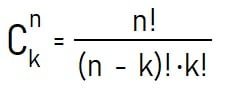
Baca Juga: Perbedaan Penggunaan Rumus Permutasi dan Kombinasi
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Nilai n pada Notasi Faktorial
Jika nC4 = n2 ‒ 2n maka 2nCn+3 = ….
A. 101
B. 1.001
C. 1.010
D. 1.011
E. 1.100
Pembahasan:
Langkah pertama yang perlu dilakukan adalah menentukan nilai n yang sesuai dengan persamaan nC4 = n2 ‒ 2n seperti cara berikut.
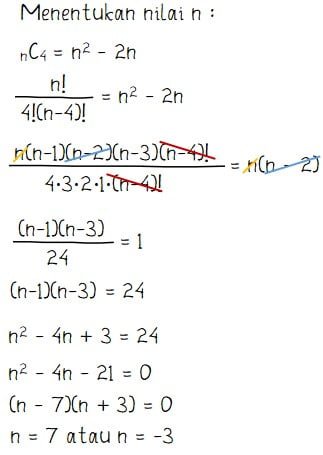
Nilai n pada notasi faktorial untuk nC4 menandakan bernilai positif, sehingga nilai n yang memenuhi adalah n = 7. Selanjutnya dapat dicari nilai 2nCn+3 = 14C10 seperti penyelesaian berikut.
14C10 = 14!/10!4!
14C10 = 14·13·12·11·10!/10!·4·3·2·1
= 14·13·12·11/4·3·2·1
= 14·13·11/2·1
= 7·13·11 = 1.001
Jadi, nilai 2nCn+3 = 14C10 = 1.001
Jawaban: B
Contoh 2 – Soal Nilai n pada Notasi Faktorial
Bentuk notasi faktorial yang sesuai untuk n(n – 1) adalah ….
A. n!
B. (n – 1)!
C. (n2 – 1)!
D. n!/(n – 1)!
E. n!/(n – 2)!
Pembahasan:
Perlu diketahui bahwa n! = n(n – 1)! = n(n – 1)(n – 2)! sehingga untuk bentuk notasi faktorial untuk n(n‒1) dapat ditentukan seperti cara berikut.
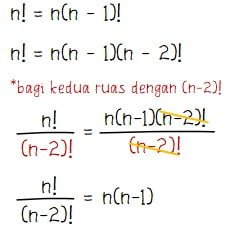
Jadi, bentuk notasi faktorial yang sesuai untuk n(n – 1) adalah n!/(n – 2)!
Jawaban: E
Contoh 3 – Soal Nilai n pada Notasi Faktorial

Pembahasan:
Perlu diingat kembali bahwa n! = n×(n‒1)×(n‒2)× … ×3×2×1 di mana (n‒1)×(n‒2)× … ×3×2×1 = (n-1)! Sehingga dapat disimpulkan bahwa n! = n×(n‒1)! atau n! = n×(n‒1)×(n‒2)! Bentuk-bentuk persamaan tersebut akan berguna untuk mendapatkan bentuk sederhana dari persamaan dengan notasi faktorial seperti pada soal.
Bentuk paling sederhana dari persamaan seperti yang diberikan pada soal dapat ditentukan melalui beberapa operasi berikut.
n!(n‒2)!/(n-3)!(n-1)! = n(n-1)!(n‒2)(n‒3)!/(n-3)!(n-1)!
= n(n-1)!(n‒2)(n‒3)!/(n-3)!(n-1)!
= n(n‒2)
= n2 ‒ 2n
Jadi, bentuk sederhana dari persamaan dengan notasi faktorial seperti pada soal adalah n(n – 2) = n2 ‒ 2n.
Jawaban: C
Demikianlah tadi ulasan bagaimana cara menentukan nilai n pada notasi faktorial. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Peluang Kejadian Majemuk dan Bersyarat
