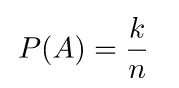Teori peluang adalah cabang ilmu matematika yang membahas tentang kemungkinan terjadinya suatu peristiwa/kejadian. Bahasan dalam materi peluang antara lain meliputi peluang kejadian majemuk (saling lepas dan saling bebas), peluang kejadian bersyarat, dan peluang tanpa/dengan pengembalian. Contoh peluang sering digunakan untuk menyatakan prediksi, misalnya peluang besok akan turun hujan. Di mana, ada 2 kemungkinan yang akan terjadi yaitu besok benar akan hujan atau besok tidak hujan.
Besar peluang dinyatakan dalam rentang nilai 0 sampai dengan 1. Nilai peluang 0 menunjukkan kemustahilan (ketidak mungkinan), sedangkan nilai 1 mengindikasikan kepastian akan terjadinya suatu peristiwa. Dengan kata lain, semakin besar nilai peluang mendekati angka 1 maka kemungkinan pasti akan terjadi lebih besar. Sedangkan untuk semakin nilai mendekati 0 artinya kejadian semakin besar untuk tidak akan terjadi.
o ≤ P(A) ≤ 1
Ruang lingkup bahasan peluang meliputi bagaimana cara menentukan banyak ruang sampel dan kejadian yang mungkin. Apa itu ruang sampel? Bagaimana cara menentukan banyaknya kejadian yang terjadi? Bagaimana cara menentukan besar peluang kejadian majemuk dan bersyarat? Sobat idschool dapat mencari tahu lebih banyak melalui ulasan peluang kejadian majemuk dan bersyarat di bawah.
Table of Contents
- Ruang Sampel dan Frekuensi Harapan
- Peluang Komplemen Suatu Kejadian
- Peluang Kejadian Majemuk
- Peluang Kejadian Bersyarat
- Contoh Soal dan Pembahasan
Ruang Sampel dan Frekuensi Harapan
Ruang sampel mencakup semua/seluruh kejadian yang mungkin terjadi, banyaknya ruang sampel disimbolkan dengan n(S). Contohnya, pada pelemparan sekeping uang logam yang memiliki dua permukaan yaitu sisi gambar dan angka. Banyaknya ruang sampel yang dimiliki oleh sekeping uang logam adalah n(S) = 2.
Contoh lainnya adalah pada pelemparan dua buah dadu, banyaknya ruang sampel yang akan dibentuk berjumlah 36. Sebanyak 36 ruang sampel pada pelemparan dua buah mata dadu meliputi nilai-nilai berikut.

Ruang sampel memuat semua kejadian yang mungkin terjadi, sedangkan peluang memuat kejadian yang terjadi dibanding seluruh kemungkinan kejadian yang terjadi.
Misalkan dalam suatu percobaan A, kejadian yang terjadi disimbolkan dengan k dan seluruh kejadian (ruang sampel) dilambangkan dengan n. Besar peluang kejadian A dapat dihitung melalui persamaan berikut.
Besar peluang merupakan nilai persentase dari kemungkian terjadinya sebuah kejadian/peristiwa. Banyaknya kemungkinan dari suatu kejadian bakal terjadi dinyatakan dalam nilai frekuensi harapan. Di mana, nilai frekuensi harapan diperoleh dari perkalian antara peluang dengan banyaknya percobaan.
Misalkan diketahui peluang munculnya angka dari pelemparan sebuah mata uang logam adalah 1/5. Percobaan pelemparan mata uang logam dilakukan sebanyak 310 kali. Maka, frekuensi harapan munculnya angka dalam kejadian tersebut adalah 1/5× 310 = 62.
Secara umum, frekuensi harapan terjadinya A dalam m kali percobaan dituliskan dalam rumus berikut.
F = P(A) × m
frekuensi harapan
Keterangan:
F = frekuensi harapan terjadinya suatu kejadian
P(A) = besar peluang terjadinya kejadian A
m = banyaknya percobaan
Baca Juga: Aturan Pengisian Tempat (Filling Slots)
Peluang Komplemen Suatu Kejadian
Peluang komplemen suatu kejadian berarti menunjuk peristiwa yang sebaliknya atau kejadian yang berkebalikan dengan kejadian yang diharapkan. Misalnya pada peluang kejadian A, kejadian tidak terjadinya kejadian A disebut dengan komplemen kejadian A dan disimbolkan AC.
Diketahui bahwa jumlah terjadinya suatu kejadian dan tidak terjadinya suatu kejadian sama dengan besar seluruh kemungkinan. Sehingga antara kejadian A dan komplemen kejadian AC memiliki hubungan yang sesuai dengan rumus berikut.
P(AC) = 1 ‒ P(A)
Misalnya, P(A) adalah besar peluang kejadian besok Hari Minggu akan hujan dan P(AC) adalah peluang besok Hari Minggu tidak hujan. Jika besar nilai peluang kejadian hujan P(A) = 0,78 maka peluang gagal atau tidak terjadinya hujan adalah P(AC) = 1 – 0,78 = 0,22.
Baca Juga: Pengertian/Perbedaan Permutasi dan Kombinasi
Peluang Kejadian Majemuk
Peluang kejadian majemuk merupakan bahasan peluang dari kemungkinan terjadinya dua kejadian. Misalkan A dab B adalah dua buah kejadian yang terdapat dalam ruang sampel S. Besar peluang kejadian majemuk A ∪ B dapat ditentukan dengan rumus peluang kejadian majemuk berikut.

Contoh soal peluang kejadian majemuk:
Satu buah kartu diambil dari satu paket kartu remi tanpa joker. Peluang terambilnya kartu King atau kartu berwarna hitam adalah ….
Penyelesaian:
Diketahui bahwa jumlah satu paket kartu remi tanpa joker adalah 52 kartu, sehingga banyaknya ruang sampel adalah n = 52.
A= kejadian terambil satu kartu king = 4 kartu king (dalam satu paket)
P(A) = 4/52
P(A) = 1/13
B= kejadian terambil satu kartu berwarna hitam = 26 berwarna hitam kartu (dalam satu paket)
P(A) = 26/52
P(A) = 1/2
A ∩ B = kejadian terambil satu kartu king warna hitam
P( A ∩ B) = 2/52
P( A ∩ B) = 1/26
Peluang terambilnya kartu king atau kartu berwarna hitam adalah:
P( A ∪ B) = P(A) + P(B) ‒ P(A ∩ B)
P( A ∪ B) = 1/13 + 1/2 ‒ 1/26
P( A ∪ B) = 2/26 + 13/26 ‒ 1/26
P( A ∪ B) = 14/26
P( A ∪ B) = 7/13
Baca Juga: Aturan Pengisian Tempat (Filling Slots)
Peluang Kejadian Majemuk yang Saling Lepas
Peluang kejadian majemuk dapat terjadi pada dua kejadian yang tidak dapat terjadi secara bersamaan. Dua kejadian dalam suatu percobaan yang masing-masing kejadian tidak mungkin terjadi bersama-sama dikatakan saling lepas. Misalkan dua kejadian tersebut dinyatakan dalam kejadian A dan kejadian B, rumus peluang kejadian mejemuk saling lepas sesuai persamaan berikut.

Contoh soal peluang kejadian majemuk saling lepas:
Peluang terambilnya satu kartu diamond atau kartu berwarna hitam dari tumpukan satu paket kartu remi tanpa joker adalah ….
Penyelesaian:
Dua kejadian berupa terambilnya kartu diamond berwana merah dan kartu berwarna hitam merupakan kejadian yang saling lepas. Alasannya adalah karena kartu diamond tidak ada yang berwarna hitam dan tidak ada kartu berwarna hitam yang merupakan diamond.
Ada dua kejadian yang diharapkan ada dua yaitu muncul kartu diamond atau muncul kartu berwarna hitam. Penyelesaian contoh soal kejadian majemuk saling lepas pada soal dilakukan seperti pada cara berikut.
A: kejadian terambil satu kartu diamond
P( A ) = 13/52
P( A ) = 1/4
B: kejadian terambil satu kartu berwarna hitam
P(B) = 26/52
P(B) = 1/2
Peluang kejadian majemuk terambilnya satu kartu diamond atau kartu berwarna hitam:
P( A ∪ B) = P(A) + P(B)
P( A ∪ B) = 1/4 + 1/2
P( A ∪ B) = 1/4 + 2/4
P( A ∪ B) = 3/4
Baca Juga: Cara Menghitung Rata-Rata (Mean) dari Data Kelompok
Peluang Kejadian Majemuk yang Saling Bebas
Dua kejadian dalam suatu percobaan dikatakan sebagai peluang kejadian majemuk saling bebas jika kejadian A mempengaruhi kejadian B, atau sebaliknya. Misalnya pada kejadian pelemparan koin, pada pelemparan pertama muncul angka kemudian pada pelemparan ke dua muncul sisi mata uang yang sama.
Rumus untuk menentukan peluang kejadian majemuk saling bebas diberikan seperti pada persamaan di bawah.

Contoh soal peluang kejadian majemuk saling bebas:
Dari pelemparan dua keping uang logam yang dilemparkan satu kali, peluang munculnya sisi gambar pada mata uang pertama dan angka pada mata uang kedua muncul sisi mata uang yang sama adalah ….
Penyelesaian:
Banyaknya ruang sampel, kejadian muncul sisi gambar pada mata uang pertama, dan kejadian muncul sisi angka pada mata uang kedua ditentukan seperti cara berikut.
Ruang sampel dari 2 keping uang logam:
n(S) = {(G, G), (G,A), (A,G), (A,A)}
n(S) = 4
A: Kejadian munculnya sisi gambar pada mata uang pertama.
n(A) = {(G, G), (G,A)} = 2
P(A) = n(A)/n(S)
P(A) = 2/4
P(A) = 1/2
B: Kejadian munculnya sisi mata uang yang sama untuk kedua mata uang tersebut.
n(B) = {(G,G), (A, A)} = 2
P(B) = n(B)/n(S)
P(B) = 2/4
P(B) = 1/2
Kejadian A ∩ B:
P (A ∩ B) = P(A) × P(B)
P (A ∩ B) = 1/2 × 1/2
P (A ∩ B) = 1/4
Jadi, peluang munculnya sisi gambar pada mata uang pertama dan pada mata uang ke dua muncul sisi mata uang yang sama adalah 1/4.
Baca Juga: Operasi Hitung Bilangan dengan Notasi Faktorial
Peluang Kejadian Bersyarat
Peluang kejadian bersyarat merupakan peluang suatu kejadian yang didahului dengan suatu kejadian yang disyaratkan. Contoh permasalahan terdapat pada pelemparan dua keping uang secara bersamaan, peluang kejadian bersayarat pada kejadian munculnya sisi angka pada satu keping uang dan munculnya sisi angka pada keping uang lainnya.
Contoh lainnya adalah peluang munculnya bilangan prima pada sebuah pelemparan dadu dengan 6 sisi jika sudah diketahui bahwa hasil yang muncul adalah bilangan ganjil.
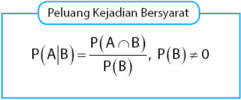
Rumus peluang munculnya kejadian A dengan syarat kejadian B telah muncul dapat dilihat pada persamaan di bawah.
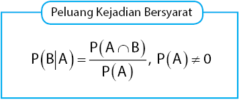
Rumus peluang munculnya kejadian B dengan syarat kejadian A telah muncul adalah:
Contoh peluang kejadian bersyarat:
Peluang munculnya bilangan ganjil pada satu kali pelemparan dadu dengan enam sisi jika diketahui telah muncul bilangan prima adalah ….
Penyelesaian:
A : kejadian munculnya mata dadu dengan bilangan ganjil
n(A) = { 1, 3, 5}
P(A) = n(A)/n(B)
P(A) = 3/6
P(A) = 1/2
B : kejadian munculnya mata dadu dengan bilangan prima
n(B) = {2, 3, 5} = 3
P(B) = n(A)/n(S)
P(B) = 3/6
P(B) = 1/2
A ∩ B: kejadian munculnya bilangan prima ganjil
A ∩ B = { 3, 5}
n( A ∩ B ) = 2
P(A ∩ B) = n(A∩B)/n(S)
P(A ∩ B) = 2/6 = 1/3
Peluang munculnya bilangan ganjil jika diketahui telah muncul bilangan prima:
P(A|B) = P(A∩B)/P(B)
P(A ∩ B) = ⅓/½
P(A ∩ B) = 1/3
Baca Juga:
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan peluang kejadian majemuk dan bersyarat. Setiap contoh soal peluang kejadian majemuk dan bersyarat yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan cara menentukan peluang kejadian majemuk dan bersyarat tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Peluang Pengambilan Tanpa Pengembalian
Dalam sebuah kotak terdapat 4 bola merah dan 5 bola kuning. Dari kotak tersebut akan diambil 3 buah bola satu per satu tanpa pengembalian. Peluang terambil bola pertama kuning, bola kedua kuning, dan bola ketiga merah adalah …
A. 5/9
B. 4/7
C. 5/18
D. 3/14
E. 10/63
Pembahasan:
Banyaknya ruang sampel:
n(S) = banyak bola merah + banyak bola kuning
n(S) = 4 + 5
n(S) = 9
A : kejadian terambilnya sebuah bola kuning pada pengambilan pertama
n(A) = 5
P(A) = n(A)/n(S)
P(A) = 5/9
B: kejadian terambilnya sebuah bola kuning pada pengambilan kedua
P(B | A) = 4/8
P(B | A) = 1/2
C: kejadian terambilnya sebuah bola merah pada pengambilan ketiga
P( C|A,B ) = 4/7
Menghitung peluang terambilnya bola pertama kuning, bola kedua kuning, dan bola ketiga merah:
P( A ∩ B ∩ C ) = P(A) × P( B|A ) × P( C|A,B )
P( A ∩ B ∩ C ) = 5/9 × 1/2 × 4/7
P( A ∩ B ∩ C ) = 10/63
Jadi, peluang terambil bola pertama kuning, bola kedua kuning, dan bola ketiga merah adalah 10/63.
Jawaban: E
Contoh 2 – Soal Peluang Pengambilan Tanpa Pengembalian
Dalam sebuah kotak terdapat 4 bola merah dan 3 bola hitam. Dari dalam kotak tersebut diambil satu buah bola pertama dan satu buah bola kedua secara berturut-turut tanpa pengembalian. Peluang terambilnya bola pertama merah dan bola kedua putih adalah ….
A. 2/7
B. 3/7
C. 5/7
D. 2/5
E. 3/5
Pembahasan:
Banyaknya ruang sampel:
n(S) = banyak bola merah + banyak bola hitam
n(S) = 4 + 3
n(S) = 7
A : kejadian terambilnya sebuah bola merah pada pengambilan pertama
P(A) = 4/7
B : kejadian terambilnya sebuah bola hitam pada pengambilan kedua
P( B|A ) = 3/6
P( B|A ) = 1/2
Dengan demikian peluang terambilnya bola pertama merah dan bola kedua hitam adalah:
P( A ∩ B ) = P (A) × P( B|A )
P( A ∩ B ) = 4/7 × 1/2
P( A ∩ B ) = 2/7
Jawaban: A
Contoh 3 – Peluang Pengambilan dengan Pengembalian
Dalam sebuah kotak terdapat 3 bola merah dan 5 bola putih. Dari dalam kotak tersebut diambil satu buah bola pertama kemudian dikembalikan lagi ke dalam kotak. Kemudian akan diambil lagi sebuah bola ke dua. Peluang terambilnya bola pertama merah dan bola kedua putih adalah ….
A. 15/256
B. 13/256
C. 15/128
D. 13/64
E. 15/64
Pembahasan:
A : Kejadian terambilnya sebuah bola merah pada pengambilan pertama
P(A) = 3/8
B : kejadian terambilnya sebuah bola putih pada pengambilan kedua
P(B) = 5/8
Peluang terambilnya bola pertama merah dan bola kedua putih:
P( A∩ B ) = P(A) × P( B | A )
P( A ∩ B ) = 3/8 × 5/8
P( A ∩ B ) = 15/64
Jawaban: E
Sekian pembahasan mengenai peluang kejadian majemuk dan bersyarat, terimakasih telah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Rumus dan Cara Menghitung Desil/Persil dari Data Kelompok