Bahasan permutasi dan kombinasi termasuk dalam kaidah pencacahan yang juga memuat pembahasan aturan pengisianatau filling slot. Perbedaan permutasi dan kombinasi terletak pada bagaimana urutan mempengaruhi banyak cara atau susunan. Permutasi membahas bagaimana penyusunan k objek dari n objek yang tersedia dengan memperhatikan urutannya. Sedangkan kombinasi membahas bagaimana penyusunan k objek dari n objek yang tersedia tanpa memperhatikan urutannya.
Contoh permasalahan yang diselesaikan dengan permutasi adalah pemilihan pengurus organisasi yang terdiri adari ketua, wakil ketua, sekretaris, dan bendahara. Contoh permasalahan yang diselesaikan dengan kombinasi adalah pemilihan beberapa orang secara acak dari orang-orang dalam suatu kelompok.

Baca Juga: Aturan Pengisian Tempat (Filling Slots)
Bagaimana cara mengenali masalah yang menggunakan permutasi? Bagaimana cara mengenali masalah yang menggunakan kompisnasi? Apa saja contoh permasalahan pada bahasan perbedaan permutasi dan kombinasi? Sobat idschool dapat mencari tahu jawabannya melalui ulasan perbedaan permutasi dan kombinasi di bawah.
Table of Contents
- Rumus Permutasi
- Rumus Kombinasi
- Perbedaan Permutasi dan Kombinasi
- Contoh Soal Perbedaan Permutasi dan Kombinasi (+Pembahasan)
Rumus Permutasi
Rumus permutasi menyelesaikan bagaimana cara menyusun objek dari n objek dengan memperhatikan urutan. Terdapat tiga macam permutasi yang diketahui yaitu permutasi dari unsur-unsur yang berbeda, permutasi dengan beberapa unsur yang sama, dan permutasi siklik. Penjelasan dari ketiga macam permutas dijelaskan lebih banyak melalui ulasan di bawah,
- Permutasi dari unsur-unsur yang berbeda yaitu banyaknya cara untuk menyusun k unsur dari n unsur yang berbeda.
- Permutasi dengan beberapa unsur yang sama yaitu banyaknya cara untuk menyusun unsur a dan b dari n unsur yang tersedia.
- Permutasi Siklik adalah cara menyusun n unsur yang susunannya membentuk lingkaran.
Baca Juga: Notasi Faktorial dan Penjelasan Masalah 0! = 1
Rumus Kombinasi
Rumus kombinasi digunakan untuk menentukan banyak cara atau susunan yang tidak memperhatikan urutan. Contoh permasalahan yang menggunakan kombinasi adalah mengetahui banyaknya cara untuk mengambil 3 bola dari 5 bola merah dan 2 bola hijau yang tersedia dalam sebuah kotak. Cara pengambilan bola tersebut tersebut bola merah, merah, dan kuning. Cara pengambilan lain yang mungkin adalah merah, kuning merah, dan lain sebagainya
Misalkan bola warna merah tersebut diberi nomor satu sampai dengan lima dan bola kuning juga diberi nomor satu sampai dua. Cara pengambilan bola pertama berwarna merah dengan nomor dua akan sama dengan terambilnya bola warna merah dengan nomor satu. Begitu pula dengan bola dengan warna dan nomor yang berlainan.
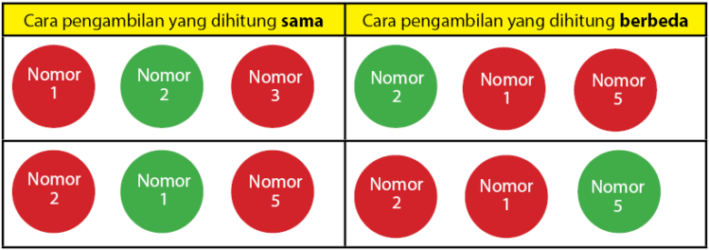
Banyaknya kombinasi k unsur yang diambil dari n unsur yang tersedia dapat diperoleh melalui rumus kombinasi seperti pada persamaan di bawah.

Baca Juga: Rumus Nilai Rata-Rata Gabungan dari 2 Data Kelompok
Perbedaan Permutasi dan Kombinasi
Setelah mengetahui dua rumus tentang permutasi dan kombinasi, hal yang tidak kalah penting adalah mengetahui perbedaan permutasi dan kombinasi. Permasalahan biasanya disajikan dalam bentuk soal cerita dan sobat idschool dituntut agar bisa membedakan masalah tersebut termasuk permutasi atau kombinasi. Sehingga, tidak terjadi kesalahan dalam menggunakan rumus permutasi/kombinasi.
Perhatikan dua contoh kasus yang menunjukkan perbaadaan permutasi dan kombinasi berikut.
Kasus pertama: permasalahan permutasi
Susunan panitia yang terdiri atas ketua, wakil ketua, sekretaris, dan bendahara akan dibentuk untuk mensukseskan suebuah acara. Susunan panitia tersebut akan dipilih dari 10 orang terpilih berdasarkan kriteria yang telah ditentukan. Berapakah banyaknya susunan panitia yang dapat dibentuk?
Kasus ke dua: permasalahan kombinasi
Enam buku akan dipilih dari lima buku Matematika, tiga buku Fisika, dan empat buku Kimia untuk disumbangkan ke sekolah untuk anak jalanan. Berapakah banyaknya cara yang dapat dilakukan untuk memilih enam buku tersebut?
Pada kasus pertama, susunan urutan menjadi bagian yang perlu diperhatikan. Kedudukan ketua untuk orang pertama tentu akan berbeda dengan ketua yang ditempati oleh orang ke tiga. Begitu juga dengan kududukan untuk posisi lainnya.
Sedangkan pada contoh kasus kedua, pemilihan buku pada urutan pertama dan kedua misalnya adalah buku Matematika pertama dan buku Matematika ke dua, keduanya merupakan buku Matematika. Sehingga, urutan tidak dipehatikan.
Itulah tadi ulasan perbedaan permutasi dan kombinasi pada suatu permasalahan. Ringkasnya, rumus permutasi digunakan untuk permasalahan yang memperhatikan urutan. Sedangkan kombinasi digunakan untuk menyelesaikan permasalahan yang tidak memperhatikan urutan.
Baca Juga: Cara Menentukan Peluang Suatu Kejadian
Contoh Soal Perbedaan Permutasi dan Kombinasi (+Pembahasan)
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan perbedaan permutasi dan kombinasi di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana menentukan perbedaan permutasi dan kombinasi. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Permutasi
Banyaknya susunan huruf yang dapat dibentuk dari kata NASIONAL adalah ….
A. 1.080 cara
B. 6.720 cara
C. 10.080 cara
D. 20.160 cara
E. 30.320 cara
Pembahasan:
Unsur-unsur yang sama pada kata “NASIONAL”:
N = 2, dan A = 2
Banyaknya susunan huruf yang berbeda :
P = 8!/2!×2!
P = 8·7·6·5·4·3·2!/2!×2!
P = 8·7·6·5·4·3/2!
P = 8·7·6·5·4·3/2·1
P = 4 × 6 × 7 × 5 × 4 × 3
P = 10.080
Jadi, banyaknya susunan huruf yang dapat dibentuk dari kata NASIONAL adalah 10.080 cara.
Jawaban: C
Contoh 2 – Soal Kombinasi
Dalam sebuah kelas terdiri atas 7 murid perempuan dan 3 murid laki-laki. Dari kelas tersebut akan dipilih 3 orang murid secara acak, maka peluang bahwa yang terpilih ketiga-tiganya perempuan adalah …
A. 2/7
B. 3/12
C. 7/24
D. 12/35
E. 11/36
Pembahasan:
Dalam permasalahan ini, urutan tidak menjadi hal yang perlu diperhatikan, sehingga rumus yang digunakan adalah kombinasi.
Banyaknya cara untuk memilih 3 murid dari 10 murid secara acak (misalkan dengan variabel n):
n = 10C3
n = 10!/7! × 3!
n = 10·9·8·7!/7! × 3!
n = 10·9·8/3!
n = 10·9·8/3·2·1 = 120
Banyaknya cara untuk memilih 3 murid perempuan dari 7 murid perempuan (misalkan dengan variabel k):
k = 7C3
k = 7!/4! × 3!
k = 7·6·5·4!/4! × 3!
k = 7·6·5/ 3!
k = 7·6·5/3·2·1
k = 7·6·5/6 = 35
Peluang bahwa yang terpilih ketiga-tiganya perempuan adalah:
P(3pi) = k/n
P(3pi) = 35/120
P(3pi) = 7/24
Jawaban: A
Sekian pembahasan mengenai pengertian/perbedaan permutasi dan kombinasi. Terima kasih sudah mengunjungi idschool(dot)net, Semoga Bermanfaat!
Baca Juga: Cara Menghitung Desil dan Persil dari Data Kelompok



