Menyederhanakan bilangan bentuk akar adalah suatu proses aljabar untuk mendapatkan bilangan dengan bentuk yang lebih mudah untuk dihitung. Biasanya, cara menyederhanakan bentuk akar terdapat operasi bilangan rasional dengan bentuk akar. Bilangan irasional adalah bilangan real yang tidak dapat dinyatakan dalam bentuk bilangan pecahan. Contoh bilangan irasional yang memiliki bentuk akar adalah √2, √3, 5√7, dan lain sebagainya.
Proses menyederhanakan bentuk akar dilakukan dengan mengubah satu bentuk akar dari suatu bilangan ke dalam bentuk akar lainnya. Menyederhanakan bentuk akar akan membuat bentuk akar dari suatu bilangan berubah, namum penyederhanaan bentuk akar tidak membuat nilanya berubah, Misalnya pada bilangan dengan bentuk akar √80 memiliki bentuk lebih sederhana menjadi bentuk 4√5.
Menyederhanakan bentuk akar dapat dilakukan Proses menyederhanakan bentuk akar pada umumnya dilakukan dengan cara mengalikan bentuk sekawan. Selain itu dalam proses menyederhanakan bentuk akar juga meliputi pengerjaan operasi aljabar dan penggunaan sifat-sifat bilangan bentuk akar.
Langkah apa saja yang dilakukan untuk menyederhanakan bentuk akar? Bagimana cara menyederhanakan bentuk akar? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Baca Juga: Operasi Hitung Aljabar
Merasionalkan Bentuk Akar (Mengalikan dengan Akar Sekawan)
Bilangan bentuk akar yang dapat merasionalkan suatu bilangan bentuk akar disebut akar sekawan. Pasangan antara bentuk akar dan bentuk akar sekawannya akan menghasilkan suatu bilangan rasional.
Bentuk akar sekawan menyesuaikan bilangan bentuk akar. Misalnya: akar sekawan untuk √a adalah √a, sementara akar sekawan untuk √a + √b adalah √a − √b.
Selaian dua bentuk akar dan akar sekawan yang telah disebutkan, masih ada beberapa bentuk pasangan akar sekawan lainnya. Secara umum, pasangan bentuk akar dan akar sekawannya terdapat pada tabel berikut.
Perkalian antara bilangan bentuk akar √a dengan akar sekawannya √a dapat menghasilkan bilangan rasional (bilangan yang memiliki bentuk pecahan). Misalnya pada perkalian dua bilangan irasional √2 × √2 memiliki hasil sama dengan 2.
Diketahui bahwa √2 adalah bilangan irasional, sedangkan 2 adalah bilangan rasional. Proses perkalian yang membuat bilangan irasional menjadi bilangan rasional disebut sebagai cara merasionalkan bentuk akar.
Contoh akar sekawan dari √2 adalah √2, akar sekawan dari √3 adalah √3, dan lain sebagainya. Contoh lainnya, akar sekawan dari (3 + √2) adalah (3 − √2).
Perkalian antara bentuk akar (3 + √2) dengan pasangan akar sekawan (3 − √2) menghasilkan bilangan rasional. Cara merasionalkan bentuk akar dilakukan seperti proses berikut.
Bentuk akar: (3 + √2)
Akar sekawan: (3 − √2)
Merasionalkan bentuk akar:
(3 + √2)×(3−√2) = 3(3−√2) + √2(3−√2)
= 32−3√2+3√2−(√2)2
= 9 − 2 = 7
Diperoleh hasil 7, di mana bilangan tujuh merupakan bilangan rasional. Merasionalkan bentuk akar dibutuhkan pada cara menyederhanakan bentuk akar untuk pecahan dengan penyebut berupa bentuk akar.
Bentuk umum pada cara menyederhanakan bentuk akar untuk pecahan bentuk-bentuk tertentu dilakukan seperti persamaan-persamaan berikut.
Baca Juga: Persamaan dan Pertidaksamaan Eksponen
Sifat-Sifat Bentuk Akar
Sifat-sifat bilangan bentuk akar juga dibutuhkan dalam cara menyederhanakan bentuk akar. Penggunaan sifat-sifat bentuk akar dibutuhkan dalam proses operasi aljabar.
Sifat-sifat pada bentuk akar memuat bagaimana cara melakukan operasi hitung bilangan dengan bentuk akar. Beberapa sifat bilangan bentuk akar terdapat pada persamaan-persamaan berikut.
Contoh penggunaan sifat-sifat bentuk akar:
1.) ⅓√8 = 3√81 = 3√8 = 2
2.) √a × √a = √22 = 2
3.) √12 × √3 = √36 = 6
4.) 2√36 = 36/2 = 33 = 27
5.) √18 = √(9×2) = √9 × √2 = 3√2
Bagaimana penggunaan sifat-sifat bilangan bentuk akar untuk menyederhanakan bentuk akar terdapat pada tiga macam contoh berikut.
Baca Juga: Sifat Grafik Fungsi Kuadrat y = ax^2 + bx + c
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Menyederhanakan Bentuk Akar
A. 5 ‒ 5√21
B. 5 + 5√21
C. ‒5 + 5√21
D. ‒5 + √21
E. ‒5 ‒ √21
Pembahasan:
Bentuk sederhana dari persamaan bentuk akar yang diberikan dapat dicari dengan mengalikannya dengan akar sekawan. Cara mendapat bentuk paling sederhana dan cara perkalian akar sekawan dapat dilihat seperti langkah-langkah berikut.
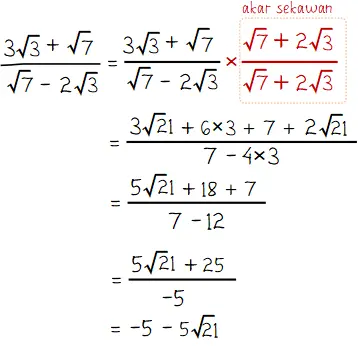
Jadi, bentuk paling sederhana dari bentuk akar di atas adalah ‒5 ‒ √21.
Jawaban: E
Contoh 2 – Soal Menyederhanakan Bentuk Akar
A. 4 ‒ 2√3
B. 2 ‒ √3
C. ‒2 + √3
D. ‒4 + √3
E. ‒4 ‒ 2√3
Pembahasan:
Langkah untuk menyederhanakan bentuk akar pada soal yang dilakukan dengan cara berikut.
Jadi, bentuk sederhana dari bentuk akar tersebut adalah 4 ‒ 2√3.
Jawaban: A
Sekian ulasan bagaimana cara menyederhanakan bentuk akar yang dapat dilakukan dengan mengalikan akar sekawan, operasi aljabar, serta sifat-sifat bentuk akar. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
