Bilangan berpangkat pecahan memiliki hubungan yang ekuivalen dengan suatu bentuk akar. Di mana, pembilang pangkat pecahan bertindak sebagai pangkat bilangan dan penyebut dari pangkat pecahan bertindak sebagai indeks akar. Dengan hubungan tersebut, selanjutnya dapat ditentukan nilai dari suatu bilangan yang memiliki pangkat pecahan. Sedangkan cara melakukan operasi hitung bilangan dengan pangkat berbentuk pecahan secara umum mengikuti aturan pada operasi hitung bilangan berpangkat (eksponen).
Contoh bentuk bilangan dengan pangkat pecahan adalah 8⅓, 16¼, a½, dan lain sebagainya. Cara menentukan nilai-nilai bilangan dengan pangkat pecahan dapat dilakukan sengan mengubahnya menjadi bentuk akar kemudian menghitungnya. Misalnya pada bilangan 8⅓ yang ekuivalen dengan bentuk akar ∛8 = 2, sehingga nilai 8⅓ = 2. Contoh lain, nilai 16¼ sama dengan = ∜16 = 2 dan a½ sama dengan √a (indeks akar = 2 biasanya tidak dituliskan), Secara umum, hubungan bilangan berpangkat pecahan dengan bentuk akarnya sesuai dengan persamaan beikut.
Selanjutnya, bagaimana jika dua buah bilangan dengan pangkat pecahan dijumlah, dikurang, dikali, dibagi, atau dilakukan bentuk operasi hitung lainnya.
Bagaimana cara melakukan operasi hitung bilangan yang memiliki pangkat berupa pecahan? Apa saja sifat-sifat dari bilangan berpangkat pecahan? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Sifat-Sifat Bilangan Berpangkat Pecahan
- Cara Menghitung Bilangan Berpangkat Pecahan
- Contoh Soal dan Pembahasan
Sifat-Sifat Bilangan Berpangkat Pecahan
Cara melakukan operasi hitung bilangan berpangkat pecahan dapat dilakukan lebih mudah dengan menggunakan/menerapkan sifat-sifatnya. Di mana, sifat-sifat operasi hitung bilangan perpangkat pecahan secara umum sama dengan sifat-sifat operashi hitung bilangan berpangkat/eksponen. Satu sifat yang penting sebagai pegangan adalah bentuk bilangan b℀ = c√ba, sedangkan sifat lainnya akan mempermudah pengerjaan.
Berikut ini adalah beberapa sifat bilangan berpangkat pecahan yang dapat digunakan untuk menyelesaikan soal bilangan yang memiliki pangkat pecahan.

Baca Juga: Cara Menentukan Satuan Bilangan Berpangkat Banyak
Cara Menghitung Bilangan Berpangkat Pecahan
Langkah menyelesaikan persamaan dengan bilangan yang memiliki pangkat berbentuk pecahan bergantung dari bentuknya. Sfat-sifat pada operasi hitung pecahan bilangan bulat berlaku juga pada bilangan dengan pangkat pecahan. Sehingga, sobat idschool bisa mengingat kembali bagaimana operasi hitung bilangan berpangkat/eksponen.
Penggunaan sifat-sifat eksponen perlu menyesuaikan bentuk dari soal yang akan diselesaikan. Beberapa soal sederhana di bawah dapat sobat idschool gunakan untuk mengetahui bagaimana cara menghitung nilai bilangan berpangkat pecahan.
Soal 1: Hasil dari 125⅔ adalah ….
A. 5
B. 15
C. 25
D. 50
Jawab: C
Soal di atas dapat diselesaikan dengan menggunakan sifat bilangan dengan pangkat pecahan. Penyelesaian operasi hitung bilangan berpangkat pecahan pada soal dilakukan melalui beberapa langkah mudah berikut.

Soal 2: Nilai dari 4½ + 8⅓ = ….
A. 2
B. 4
C. 6
D 8
Jawab: B
Cara menentukan nilai dari penjumlahan dua bilangan yang memiliki pangkat berbentuk pecahan dapat dilakukan seperti langkah-langkah berikut.
4½ + 8⅓ = (22)½ + (23)⅓
= 22×½ + 23×⅓
= 21 + 21 = 2 + 2 = 4
Baca Juga: Rumus pada Pola Bilangan 2 Tingkat
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Cara Melakukan Operasi Hitung Bilangan Berpangkat Pecahan
B. 28
C. 68
D. 78
Pembahasan:
Penyelesaian soal dengan bilangan yang memiliki pangkat pecahan seperti pada soal di atas dapat dilakukan dengan menyederhanakan bentuknya. Setelah mendapatkan bentuk paling sederhana dapat diperoleh bilangan-bilangan berpangkat yang dapat ditentukan nilainya. Cara menyelesaikan operasi hitung penjumlahan dan pengurangan pada bilangan yang memiliki pangkat pecahan seperti yang diberikan pada soal dapat dilakukan seperti cara berikut.

Jadi, hasil dari operasi hitung penjumlahan dan pengurangan bilangan berpangkat tersebut adalah 18.
Jawaban: A
Contoh 2 – Cara Melakukan Operasi Hitung Bilangan Berpangkat Pecahan
B. 35½
C. 33½
D. 32½
Pembahasan:
Penyelesaian persamaan bilangan berpangkat seperti yang diberikan pada soal dapat dilakukan melalui cara berikut.

Jawaban: A
Contoh 3 – Cara Melakukan Operasi Hitung Bilangan Berpangkat Pecahan
A. 1/a(a2 ‒ √a + 1)
B. 1/a(a2 ‒ 1)
C. 1/a(1 ‒ a2)
D. 1/a(a ‒ 1)2
E. 1/a(a2 ‒ √a)
Pembahasan:
Penyelesaian persamaan bilangan berpangkat seperti yang diberikan pada soal dapat dilakukan melalui cara berikut.
Misalkan:
p = a‒¼ ‒ a¼
q = a ‒¼ + a ¼
Melakukan operasi hitung bilangan berpangkat pecahan:
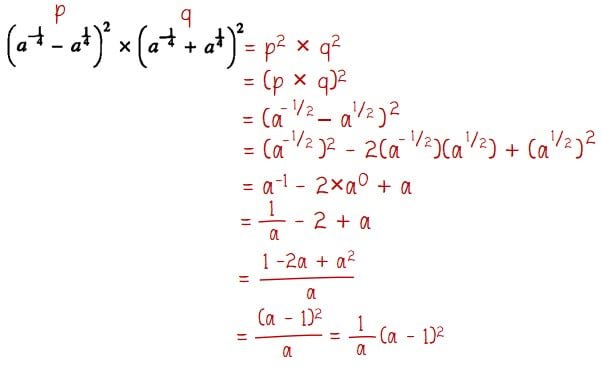
Jadi, hasil dari penyelesaian persamaan yang diberikan pada soal adalah 1/a(a ‒ 1)2
Jawaban: D
Contoh 4 – Cara Melakukan Operasi Hitung Bilangan Berpangkat Pecahan
Diketahui nilai:
a = 125
b = 27
c = 1.000
B. 6
C. 8
D. 14
E. 15
Pembahasan:
Cara menentukan nilai dari penjumlahan/pengurangan bilangan-bilangan yang memuat pangkat pecahan seperti pada soal dapat diselesaikan dengan cara berikut.
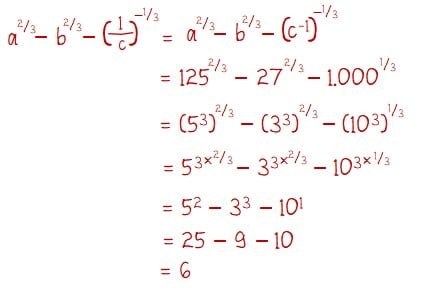
Jadi, nilai dari operasi bilangan tersebut adalah 6.
Jawaban: B
Demikianlah tadi ulasan operasi hitung bilangan berpangkat pecahan yang meliputi bahasan sifat-sifat bilangan berpangkat pecahan dan cara melakukan operasi hitungnya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menjumlahkan Pecahan


2²⁰²⁴