Sebuah kerucut yang diiris dari beberapa sudut dapat menghasilkan bentuk lingkaran, elips, hiperbola, dan parabola. Kerucut yang diiris mendatar akan membentuk lingkaran. Sedangkan kerucut yang diiris dengan kemiringan sudut tertentu akan membentuk bangun elips. Selanjutnya, irisan kerucut elips akan menjadi topik pembahasan tersendiri pada materi irisan kerucut.
Persamaan elips dipengaruhi pusat elips, sumbu mayor elips, dan sumbu minor elips. Persamaan elips dengan pusat O(0, 0) tentu akan memiliki bentuk persamaan yang berbeda dengan elips pada pusat P(a, b). Perhatikan irisan kerucut elips beserta keterangannya seperti yang diberikan pada gambar di bawah.
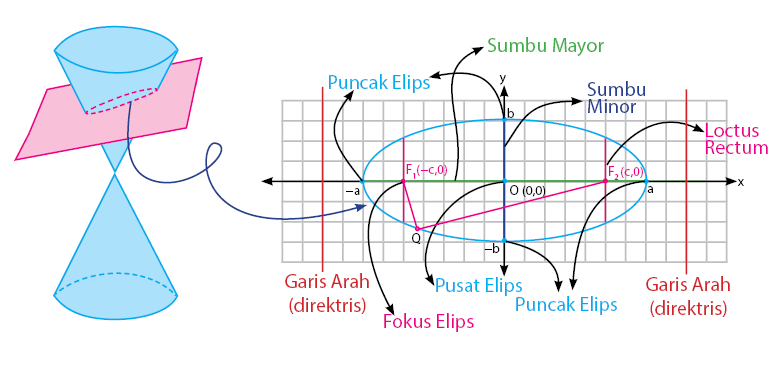
Itu dia komponen-komponen irisan kerucut dari sebuah elips. Berikutnya, akan dibahas ulasan pertama yaitu bentuk umum persamaan elips.
Bentuk Umum Persamaan Elips
Bentuk elips seperti lingkaran yang dipipihkan. Elips dibedakan menjadi dua, yaitu elips horizontal dan elips vertikal. Jika lingkaran dipihkan dari atas dan bawah maka akan terbentuk elips horizontal. Sedangkan lingkaran yang dipipihkan dari samping kanan dan kiri akan membentuk elips vertikal. Salah satu faktor penentu bentuk persamaan irisan kerucut elips adalah letak pusatnya.
Bentuk persamaan umum elips akan diberikan dalam dua topik pembahasan. Peratama adalah persamaan elips dengan pusat O(0, 0). Kedua adalah persamaan elips dengan pusat P(a, b).
Berikut ini adalah bentuk umum persamaan parabola dengan pusat O(0, 0).

Tidak jauh berbeda dengan persamaan elips dengan pusat O(0, 0). Persamaan elips pada P(a, b) deiberikan seperti tabel di bawah.

Baca Juga: Irisan Kerucut (Lingkaran, Elips, Parabola, dan Hiperbola)
Demikianlah persamaan irisan kerucut elips yang terdiri dari beberapa bentuk persamaan umum, berdasarkan letak titik pusatnya adan jenis elipsnya. Berikutnya, akan diulas cara menggambar elips jika diketahui persamaan elips dan cara menentukan persamaan elips jika diketahui gambar elips.
Cara Menggambar Persamaan Elips
Pembahasan di sini akan mengulas cara menggambar elips jika diketahui sebuah bentuk umum persamaan elips. Bentuk umum persamaan elips yang diberikan di atas akan menjadi patokan untuk membuat gambar elips.
Contoh soal menggambar elips:
Diketahui persamaan elips: 4x2 + 9y2 + 16x – 18y – 11 = 0
Bagaimanakah gambar elips yang sesuai dengan persamaan di atas?
Ubah bentuk persamaan elips yang diketahui pada soal menjadi bentuk umum persamaan elips. Tujuannya untuk mempermudah menentukan letak titik pusat, sumbu mayor, dan sumbu minor.
Caranya dapat disimak pada langkah di bawah.
4x2 + 9y2 + 16x ‒ 18y ‒ 11 = 0
4x2 + 16x + 16 + 9y2 ‒ 18 y + 9 = 11 + 16 + 9
4(x2 + 4x + 4) + 9(y2 ‒ 2y + 1) = 11 + 16 + 9
4(x + 2)2 + 9(y ‒ 1)2 = 36
Kedua ruas dibagi dengan 36 sehingga dapat diperoleh persamaan berikut.

Melalui bentuk persamaan elips seperti yang diperoleh pada hasil akhir di atas, dapat disimpulkan seperti berikut.
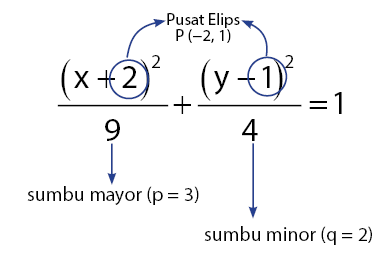
Sehingga, gambar elips yang sesuai dengan persamaan pada soal adalah seperti berikut.
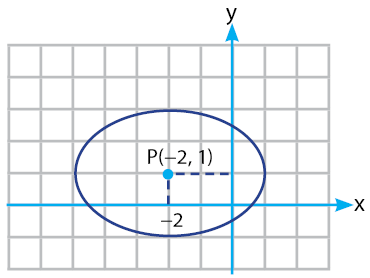
Baca Juga: Kedudukan Titik Terhadap Elips
Bagaimana? Sudah cukup jelas dengan cara menggambar elips pada ulasa di atas? Berikutnya, akan diulas cara menentukan persamaan elips dari sebuah gambar elips yang diketahui. Simak ulasan yang akan diberikan di bawah.
Cara Menentukan Persamaan Elips
Dalam beberapa pembahasan, terdapat soal yang menanyakan suatu persamaan jika diketahui sebuah gambar elips. Cara menentukan persamaan elips tersebut dapat secara mudah ditentukan dengan melihat bagian-bagian yang diketahui pada gambar elips. Selain itu, sobat idschool juga perlu mengetahui bentuk umum persamaan elips yang telah diberikan di atas.
Carilah bentuk persamaan irisan kerucut elips untuk gambar di bawah!

Untuk mendapatkan persamaan elips, pertama cari tahu terlebih dahulu informasi yang dapat diperoleh dari gambar elips pada soal. Informasi yang dapat diperoleh dari gambar elips yang diberikan pada soal meliputi pusat elips P(4, 5), bentuk elips vertikal, sumbu mayornya adalah 8, dan sumbu minornya adalah 4.
Bentuk umum persamaan irisan kerucut elips vertikal untuk pusat P(a, b), panjang sumbu mayor p, dan panjang sumbu minor q:
Sehingga, persamaan elips yang sesuai dengan soal yang diberikan adalah seperti berikut.

Selesai, diperoleh persamaan elips yang sesuai pada soal diberikan pada persamaan di atas. Demikianlah ulasan tentang irisan kerucut elips. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Kedudukan Titik Terhadap Parabola

