Matriks adalah bilangan real yang disusun dalam baris dan kolom yang berada dalam sebuah tanda kurung. Salah satu kegunaam matriks dapat berguna unutk untuk menentukan hasil komposisi transformasi geometri. Bentuk permasalahan dalam tranformasi geometri dapat meliputi beberapa kali transformasi yang dapat disebut dengan komposisi transformasi geometri.
Ada 4 bentuk transformasi geometri yang diketahui yaitu translasi (pergeseran), refleksi (pencerminan), rotasi (perputaran), dan dilatasi (perkalian). Keempat bentuk transformasi geometri tersebut memiliki suatu persamaan matriks yang dapat menunjukkan letak perubahan posisi obyek/benda. Persamaan matriks transformasi geometri nantinya berguna untuk membentuk matriks komposisi transformasi geometri. Ringkasan matriks transformasi geometri pada suatu titik untuk berbagai jenis transformasi diberikan seperti pada tabel di bawah.
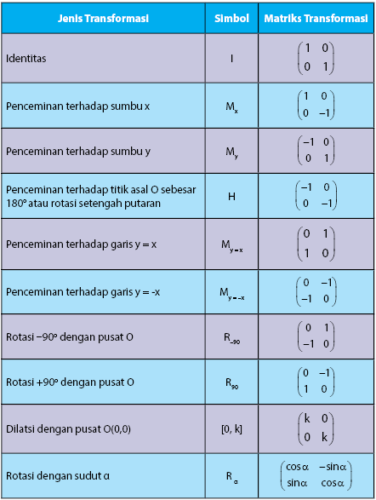
Contoh bentuk komposisi transformasi geometri adalah refleksi suatu obyek yang dilanjutkan dengan rotasi, translasi obyek yang dilanjutkan dengan refleksi, dan lain sebagainya. Bagaimana cara menyelesaian bentuk komposisi transformasi geometri? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Bentuk Matriks Hasil Komposisi Transformasi Geometri
Penyelesaian komposisi transformasi geometri dapat dilakukan dengan dengan kombinasi matriks transformasi geometri. Dengan kata lain, hasil komposisi transformasi geometri diperoleh dengan menyelesaikan perhitungan matriksnya. Hasil tranformasi suatu obyek diperoleh melalui perkalian matriks yang mewakili matriks transformasi geometrinya. Namun, peletakan matriks berkebalikan dengan proses transformasinya
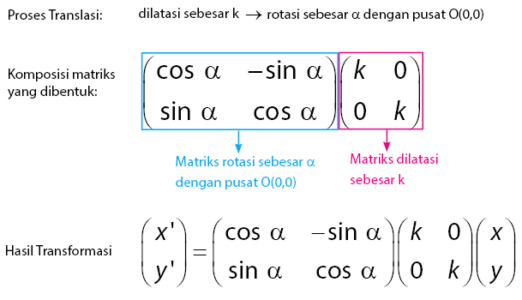
Misalkan sebuah transformasi geometri yang dinyatakan dalam dilatasi sebesar k dilanjutkan rotasi sebesar α dengan pusat O(0, 0). Maka persamaan perkalian matriks yang dibentuk adalah matriks rotasi sebesar α dengan pusat O(0, 0) dikali matriks dilatasi sebesar k.
Pembentukan matriks hasil transformasi geometri untuk permasalahan di atas sesuai dengan persamaan berikut.
Baca Juga: Operasi Hitung pada Matriks dan Sifat-sifatnya
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Matriks Komposisi Transformasi Geometri untuk Rotasi dan Refleksi
Sebuah kurva dengan persamaan y = x2 ‒ 2x ‒ 3 dirotasi sebesar 1802 dengan pusan O(0,0) yang kemudian dilanjutkan refleksi terhadap garis y = -x. Persamaan kurva hasil translasi adalah ….
A. x = y2 + 2x + 3
B. x = y2 ‒ 2y + 3
C. x = y2 ‒ 2y ‒ 3
D. y = x2 ‒ 2x + 3
E. y = x2 ‒ 2x ‒ 3
Pembahsan:
Matriks rotasi sebesar 180o dengan pusat O(0,0):

Matriks refleksi terhadap garis y = -x:

Sehingga, hasil translasi geometri dapat diperoleh dengan menyelesaikan komposisi transformasi geomteri dengan matriks seperti persamaan di bawah.

Substitusi y = x’ dan x = y’ pada persamaan y = x2 ‒ 2x ‒ 3 sehingga diperoleh persamaan kurva hasil translasi yaitu x’ = (y’)2 ‒ 2y’ ‒ 3 → x = y2 ‒ 2y ‒ 3. Jadi, diperoleh bahwa persamaan kurva hasil translasi adalah x = y2 ‒ 2y ‒ 3.
Jawaban: C
Contoh 2 – Matriks Komposisi Transformasi Geometri untuk Rotasi dan Refleksi
Bayangan kurva y = x2 ‒ 3 jika dicerminkan terhadap sumbu x dilanjutkan dengan dilatasi pusat O dan faktor skala 2 adalah ….
A. y = 1/2x2 + 6
B. y = 1/2x2 ‒ 6
C. y = 1/2x2 ‒ 3
D. y = 6 ‒ 1/2x2
E. y = 3 ‒ 1/2x2
Pembahasan:
Matriks transformasi pencerminan terhadap sumbu x:

Matriks transformasi dilatasi pusat O dan faktor skala 2:

Sehingga, dapat diperoleh matriks transformasi untuk pencerminan terhadap sumbu x dilanjutkan dengan dilatasi pusat O dan faktor skala 2 seperti cara berikut.
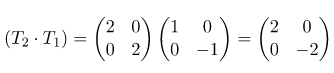
Matriks transformasi untuk menentukan bayangan:

Diperoleh dua persamaan: x = 1/2x’ dam y = ‒1/2y’, sustitusi nilai x dan y pada persamaan y = x2 ‒ 3 untuk mendapatkan hasil bayangan kurva.
Menentukan bayangan kurva:
y = x2 ‒ 3
( ‒1/2y’) = (1/2x’ )2 ‒ 3
‒1/2y’ = 1/4x’2 ‒ 3
*kalikakan kedua ruas dengan 2
‒y’ = 1/2x’2 ‒ 6
y’ = ‒1/2x’2 + 6
y’ = 6 ‒ 1/2x’2 → y = 6 ‒ 1/2x2
Jadi, bayangan kurva y = x2 ‒ 3 jika dicerminkan terhadap sumbu x dilanjutkan dengan dilatasi pusat O dan faktor skala 2 adalah y = 6 ‒ 1/2x2.
Jawaban: D
Demikianlah tadi pembahasan mengenai komposisi fungsi transformasi geometri dengan matriks. Semoga bermanfaat, terimakasih sudah mengunjungi idschool.net.
Baca Juga: Rumus Jumlah dan Selisih Dua Sudut
