Limit Tak Hingga Fungsi Trigonometri

Limit memiliki arti umum sebagai batas ambang dari suatu nilai. Sehingga, limit tak hingga memiliki pengertian bahwa suatu nilai dari persamaan yang didekati oleh nilai yang sangat besar atau tak hingga (simbol: ∞). Nilai limit tak hingga fungsi trigonometri merupakan fungsi trigonometri yang didekati oleh suatu nilai yang sangat besar.

Definisi limit menyatakan bahwa suatu fungsi f(x) akan mendekati nilai tertentu jika x mendekati nilai tertentu. Sebagai contoh, perhatikan sebuah fungsi f(x) = 2x – 5 dan nilai x mendekati 3 (x → 0). Jika x dekat 3 maka nilai fungsi f(x) = 2x – 5 akan mendekati nilai 2(3) – 5 = 6 – 5 = 1.

Jika x mendekati nilai tak hingga maka bagaimana nilai limitnya? Tentunya nilainya juga akan dekat dengan tak hingga. Pada contoh nilai f(x) = 2x – 5, jika x dekat tak hingga maka nilai f(x) juga akan mendekati nilai tak hingga.

Beberapa bentuk soal limit memuat fungsi trigonometri yang didekati oleh nilai tak hingga (sangat besar). Bagaimana cara menentukan nilai limit tak hingga fungsi trigonometri? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Nilai Limit Tak Hingga Fungsi Trigonometri
• Cara Menentukan Nilai Limit Fungsi Trigonometri
• Contoh Soal dan Pembahasan
  • Contoh 1 – Soal Limit Tak Hingga Fungsi Trigonometri
  • Contoh 2 – Soal Limit Tak Hingga Fungsi Trigonometri
  • Contoh 3 – Soal Limit Tak Hingga Fungsi Trigonometri

Nilai Limit Tak Hingga Fungsi Trigonometri

Pada sebuah fungsi trigonometri f(x) = cos (¹/_x), jika x mendekati nilai yang sangat besar atau tak hingga maka nilai f(x) = cos (¹/_x) akan dekat terhadap cos 0 = 1. Hal tersebut dikarenakan ketika substitusi nilai x pada ¹/_x akan menghasilkan nilai yang mendaki 0. Sehingga, jika x dekat tak hingga maka nilai f(x) = cos (¹/_x) akan dekat terhadap cos 0 = 1.

Tidak semua fungsi trigonometri dapat ditentukan nilai limitnya, contohnya pada fungsi trigonometri y = cos x. Fungsi cos x memiliki nilai yang periodik. Nilai terbesar cos x adalah 1 dan nilai terkecilnya adalah –1. Nilai cos x = 1 dicapai saat besar sudut x = 0^o, 360^o, dan lain sebagainya.

Besar nilai sudut mendekati tak hingga tidak dapat menghasilkan suatu nilai cosinus yang dekat dengan nilai tersebut . Kesimpulannya, jika besar sudut x tak hingga maka nilai limit cos x tidak terdefinisi.

Bentuk soal limit x tak hingga dapat memuat fungsi nilai trigonometri yang lebih rumit dari contoh di atas. Namun, konsep dalam mencari nilai limit tak hingga fungsi trigonometri secara umum dilakukan seperti pendekatan yang diberikan pada contoh-contoh di atas.

Baca Juga: Pengertian Limit

Cara Menentukan Nilai Limit Fungsi Trigonometri

Perhatikan sebuah fungsi trigonometri y = ^{cos x}/_x. Nilai limit dari fungsi trigonometri tersebut untuk x mendekati tak hingga adalah nol. Nilai tersebut diperoleh dengan substitusi nilai tak hingga pada persamaan.

Berapapun nilai pembilang, ketika dibagi bilangan yang sangat besar (tak hingga) akan menghasilkan nilai yang mendekati nol. Sehingga dapat disimpulkan bahwa jika x dekat tak hingga maka nilai ^{cos x}/ _x  akan dekat dengan nol.

Melalui cara yang sama dapat diperoleh juga nilai limit x menuju tak hingga dari fungsi y = ^{sin x}/_x. Jika x dekat tak hingga maka nilai ^{sin x}/ _x akan dekat dengan nol.

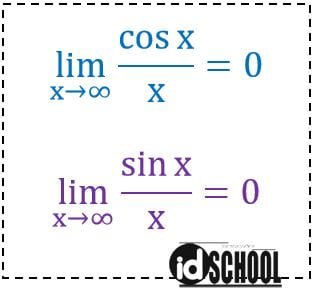
Dua persamaan nilai limit sederhana di atas akan cukup membantu dalam mengetahui nilai limit tak hingga dari suatu fungsi trigonometri yang lebih kompleks. Sebagai contoh, perhatikan cara mendapatkan nilai limit fungsi trigonometri berikut.

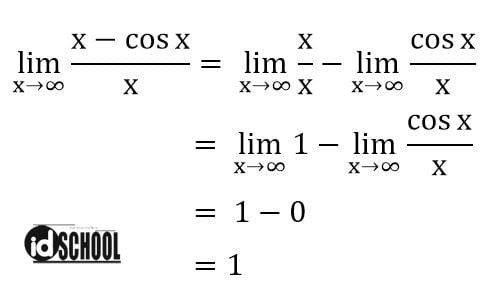
Baca Juga: Rumus Cepat Menentukan Nilai Limit Tak Hingga Untuk Beberapa Jenis Soal Tertentu

Contoh Soal dan Pembahasan

Bentuk soal limit fungsi trigonometri sangat beragam. Namun soal yang beragam tersebut dapat diselesaikan dengan bantuan konsep yang sudah dipelajari di atas dan beberapa teknik mengerjakan. Latihan soal dapat membantu mengukur pemahaman sobat idschool terhadap pemahaman sebuah materi. Selain itu, latihan soal akan menambah perbendaharaan jenis soal yang biasanya diberikan dalam ujian.

Baca Juga: 7 Tips Menentukan Nilai Limit Fungsi pada Suatu Titik

Beberapa contoh soal limit tak hingga fungsi trigonometri berikut dapat sobat idschool gunakan untuk menambah pemahaman sobat idschool. Contoh soal dilengkapi dengan pembahasan yang dapat digunakan sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih.

Contoh 1 – Soal Limit Tak Hingga Fungsi Trigonometri

Pembahasan:
Cara menentukan nilai limit tak hingga fungsi trigonometri dengan bentuk seperti pada soal dilakukan dengan mengalikan persamaan dengan ^x/_x dan mengalikannya secara aljabar. Selanjutnya akan diperoleh bentuk fungsi trigonometri yang dapat diketahui nilai limitnya seperti cara penyelesaian berikut.

Jadi, nilai limit fungsi tak hingga tersebut sama dengan 0.

Jawaban: C

Contoh 2 – Soal Limit Tak Hingga Fungsi Trigonometri

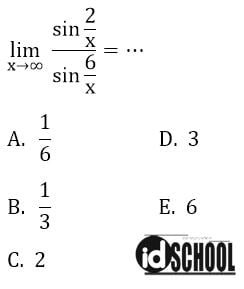
Pembasahan:
Untuk bentuk soal limit tak hingga fungsi trigonometri seperti di atas dapat ditentukan dengan memisalkan ¹/_x = α. Diketahui bahwa nilai x → ∞ maka α → ∞ untuk x → 0. Sehingga bentuk soal limit tak hingga fungsi trigonometri tersebut dapat ditentukan nilainya seperti cara berikut.

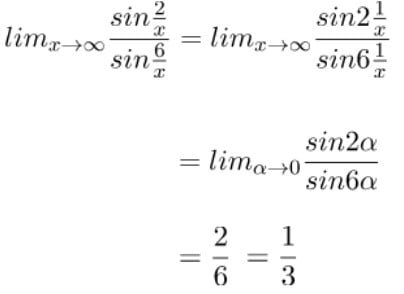
Jadi, nilai limit tak hingga fungsi trigonometri tersebut adalah ¹/₃.

Jawaban: B

Contoh 3 – Soal Limit Tak Hingga Fungsi Trigonometri

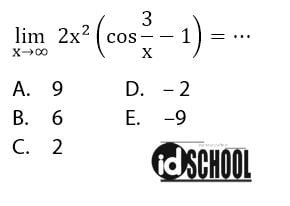
Pembahasan:
Soal limit fungsi trigonometri seperti pada soal dapat dilakukan dengan melajukan operasi aljabar dan pemisalan nilai α = ¹/_x. Sehingga nilai x = ¹/_α dengan x → ∞ maka α → 0. Soal limit tak hingga fungsi trigonometri tersebut dapat diselesaikan seperti pada cara penyelesaian berikut.

Jadi, nilai limit tak hingga fungsi trigonometri teersebut sama dengan -9.

Jawaban: E

Demikianlah tadi ulasan materi limit tak hingga fungsi trigonometri yang disertai dengan contoh cara menentukan nilai limit tak hingga fungsi trigonometri. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Kumpulan Berbagai Bentuk Soal Limit Fungsi Trigonometri