Bentuk grafik yang dihasilkan oleh fungsi kuadrat adalah kurva parabola. Gambarnya seperti huruf U (atau V), arahnya dapat terbuka ke atas atau ke bawah. Tergantung dari persamaan grafik fungsi kuadrat.
Bentuk umum fungsi kuadrat adalah f(x) = ax2 + bx + c. Nilai koefisien a dari f(x) menjadi penentu arah terbuka kurva parabola. Saat fungsi f(x) memiliki nilai a positif (a > 0), kurva parabola terbuka ke atas (parabola 1). Saat fungsi f(x) memiliki nilai a negatif (a < 0), kurva parabola terbuka ke bawah (parabola 2).

Detail lebih banyak mengenai grafik fungsi kuadrat ada di bawah.
Daftar isi:
- Grafik Fungsi Kuadrat
- Menggambar Grafik Fungsi Kuadrat
- Menggambar Grafik Fungsi Kuadrat dengan Aplikasi
- Pergeseran Kurva Parabola
Grafik Fungsi Kuadrat
Ada dua rumus yang dapat digunakan untuk menyatakan fungsi kuadrat. Kedua rumus fungsi kuadrat terdapat pada masing-masing penjelasan berikut.
1) Bentuk f(x) = ax2 + bx + c
Grafik fungsi kuadrat merupakan grafik yang simetris. Sumbu simetrinya berupa garis vertikal yang dapat dinyatakan dalam persamaan garis lurus x.
Sumbu simetri selalu menjadi absis titik puncak kurva. Persamaan kuadrat dengan bentuk umum f(x) = ax2 + bx + c memiliki koordinat titik pucak (xp, yp).
Nilai xp (absis titik puncak) dan yp (ordinat) dapat dicari menggunakan rumus berikut.
Kurva parabola dari persamaan f(x) = ax2 + bx + c dengan nilai b dan c = 0 menjadi f(x) = ax2. Bentuk grafik dengan fungsi ini simetris pada sumbu y (x = 0) dan memiliki nilai puncak di titik (0,0).
Kurva parabola dari y = ax2 + bx + c dengan nilai b =0 menjadi f(x) = ax2 + c. Bentuk grafik dari persamaan f(x) ini simetris pada sumbu y dan memiliki titik puncak di (0, c).
Grafik fungsi kuadrat hanya memiliki satu titik puncak dan satu titik potong dengan sumbu y. Sementara banyak titik potong dengan sumbu x paling banyak ada 2, bisa hanya satu, atau tidak memiliki titik potong dengan sumbu x.
Banyak titik potong parabola dengan sumbu x dapat diketahui melalui nilai diskrimian D = b2 – 4ac.
| Syarat | Banyak titik potong dengan sb-y |
| D < 0 | 0 |
| D = 0 | 1 |
| D > 0 | 2 |
2) Bentuk f(x) = a(x – xp)2 + yp
Kurva parabola yang sudah diketahui letak koordinat titik puncaknya dapat dinyatakan melalui persamaan f(x) = a(x – xp)2 + yp. Contoh, grafik fungsi kuadrat dengan titik puncak (1, -9) memiliki persamaan f(x) = a(x – 1)2 – 9.
Tidak ada perbedaan dari parabola yang dinyatakan dalam f(x) = ax2 + bx + c atau f(x) = a(x – xp)2 + yp. Rumus ini digunakan sesuai kebutuhan.
Baca Juga: Sketsa Grafik Fungsi Kuadrat
Menggambar Grafik Fungsi Kuadrat
Saat menggambar grafik fungsi kuadat membutuhkan beberapa titik penting. Cara menggambar grafik fungsi kuadrat hanya perlu menghubungkan titik-titik penting ini.
Langkah-langkah menggambar grafik fungsi kuadrat:
- Menentukan titik potong dengan sumbu x
- Menentukan titik potong dengan sumbu y
- Mencari letak sumbu simetri
- Menentukan letak koordinat titik puncak
- Menghubungkan titik-titiknya
Sebagai contoh, perhatikan caranya pada penyelesaian soal di bawah.
Soal:
Gambarlah grafik fungsi f(x) = x2 – 2x – 8!
1. Menentukan titik potong dengan sumbu x
Titik potong dengan sumbu x terjadi ketika y = 0 atau saat nilai fungsi f(x) = 0. Diberikan fungsi f(x) = x2 – 2x – 8, maka titik potong dengan sumbu x terjadi saat x2 – 2x – 8 = 0.
Untuk mendapatkan nilai x yang memenuhi persamaan, lakukan pemfaktoran.
x2 – 2x – 8 = 0
(x–4)(x+2) = 0
x–4 = 0 atau x + 2 = 0
x = 4 atau x = –2
Diperoleh dua nilai x yang memenuhi yaitu yaitu x = 4 atau x = –2. Sehingga titik potong parabola dengan sumbu x terletak pada titik (4, 0) dan (-2, 0).
2. Menentukan titik potong dengan sumbu y
Titik potong dengan sumbu y terjadi ketika nilai x = 0. Untuk mendapatkan titik potong dengan sumbu y, substitusi nilai x = 0 ke persamaan fungsi f(x) sehingga diperoleh nilai f(0).
Diberikan fungsi f(x) = x2 – 2x – 8,
Maka,
f(0) = 02 – 2 · 0 – 8
f(0) = 0 – 0 – 8 = –8
Jadi, titik potong prabola dengan sumbu y adalah (0, –8).
3. Menentukan sumbu simetri
Sumbu simetri kurva parabola berupa garis lurus tak hingga yang sejajar dengan sumbu x. Dinyatakan dapat persamaan garis x.
Rumus sumbu simetri dari kurva parabola:
Persamaan f(x) = x2 – 2x – 8 memiliki nilai a = 1 dan b = –2. Sehingga, sumbu simetri dari kurva parabola adalah
Diperoleh bilai xp = 1. Jadi, sumbu simeteri kurva parabola dari fungsi kuadrat f(x) = x2 – 2x – 8 adalah x = 1.
4. Menentukan letak koordinat titik puncak
Letak koordinat titik puncak dari kurva parabola dengan persamaan y = ax2 + bx + c adalah (–b/2a, b2 – 4ac/4a). Atau koordinat titik puncaknya adalah (xp, f(xp)).
Diberikan persamaan fungsi kuadrat f(x) = x2 – 2x – 8.
Sehingga,
xp = 1
f(xp) = f(1) = 12 – 2(1) – 8 = –9
Jadi, koordinat titik puncaknya adalah (1, –9) Diperoleh nilai xp = 1 dan yp = –9, sehingga letak koordinat titik pucak atau titik balik minimum dari grafik fungsi y = x2 – 2x – 8 adalah (1, –9).
5. Menghubungkan titik-titiknya
Langkah terakhir hanya perlu menghubungkan titik-titik penting yang diperoleh. Beberapa titik-titik penting ada pada tabel di bawah.
| Keterangan | Hasil |
| Titik potong demgan sumbu x | (−2,0); (4,0) |
| Titik potong dengan sb-y | (−8, 0) |
| Sumbu simetri | x = 1 |
| Titik balik minimum | (1, −9) |
Tentukan letak setiap titik-titik yang diperoleh. Hubungkan titik-titik tersebut sehingga dapat diperoleh kurva parabola seperti berikut.

Baca Juga: Cara Menentukan Persamaan Kuadrat Baru
Menggambar Grafik Fungsi Kuadrat dengan Aplikasi
Grafik yang dihasilkan oleh fungsi kuadrat dapat digambar dengan bantuan aplikasi. Nama aplikasinya adalah GeoGebra atau Mathway.
Cara menggambar grafik fungsi kuadrat dengan aplikasi sangat mudah. Caranya hanya dengan memasukkan persamaan kuadrat yang akan digambar. Sebagai contoh, lihat cara menggambar fungsi kuadrat f(x) = x2 – 2x – 8 menggunakan aplikasi Mathway.
Langkah-langkah menggambar grafik fungsi kuadrat menggunakan aplikasi:
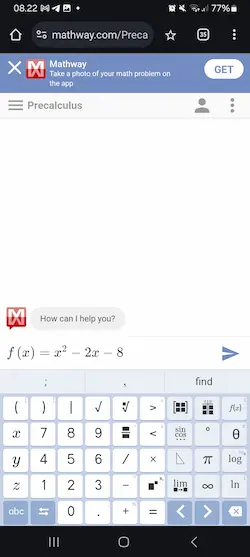
1) Buka situs mathway.com menggunakan browser atau buka aplikasinya jika sudah mengunduh dari Playstore.
2) Ketik fungsi f(x) pada kolom yang disediakan. Kemudian tekan tombol kirim.
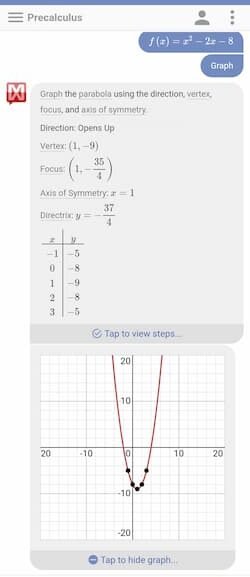
3) Akan muncul beberapa pilihan. Untuk memunculkan gambar grafiknya pilih Graph.
4) Scroll ke bawah untuk melihat hasil gambar grafiknya.
Pergeseran Kurva Parabola
Pergeseran fungsi f(x) ke kiri atau kanan membuat nilai absis berubah. Fungsi f(x) yang mengalami pergeseran ke kanan atau kiri akan membuat nilai absisnya berubah. Fungsi f(x) yang mengalami pergeseran ke atas atau bawah akan mengalami perubahan nilai ordinat.
Pergseran horizontal:
- f(x) bergeser ke kiri sebanyak a satuan → f(x) = (x + a)2
- f(x) bergeser ke kanan sebanyak a satuan → f(x) = (x – a)2
Pergeseran verikal:
- f(x) bergeser ke atas sebanyak c satuan → f(x) = x 2 + c
- f(x) bergeser ke bawah sebanyak c satuan → f(x) = x 2 – c
Sebagai contoh,
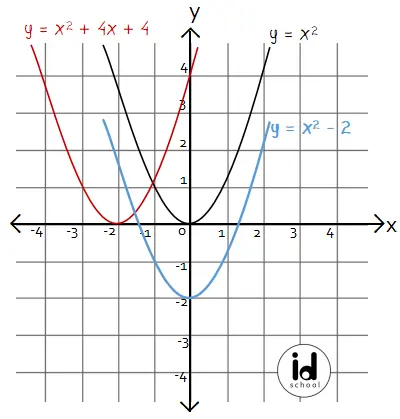
Grafik fungsi f(x) = x2 adalah parabola terbuka ke atas dengan titik puncak O(0, 0).
Kurva parabola f(x) = (x + 2)2 = x2 + 4x + 4 diperoleh dengan cara menggeser grafik fungsi f(x) = x2 ke kiri sebanyak 2 satuan. Sedangkan kurva parabola f(x) = x2 – 2 diperoleh dengan cara menggeser grafik fungsi f(x) = x2 ke bawah sebanyak 2 satuan.
Gambar grafik fungsi kuadrat y = f(x), y = x2 + 4x + 4, dan y = x2 – 2:
Demikianlah tadi ulasan grafik fungsi kuadrat yang meliputi rumus dan cara menggambar kurvanya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Mantap, sangat membantu saya😇😇👌🏻
Terimakasih atas website ini, Sangat membantu saya mengerjakan tugas
Terimakasih karena itu blogger ini saya memahami materi tersebut.
Langkah -langkah menggambar grafik Fungsi kuadrat dan contohnya
Thanks
PARAHHH LIAT INI LGSG PAHAMMMM :))
deskriminan kan yang betul
Hatur nuhun admin
makasih banayk buat blognya , sangat membantu saya
yesyesyes
aahhahahahahhahaha
aokwwaokwak kimsss
apa yang lucu?
mantap
Terimakasihh….
Luar biasa sangat membantu..
Terimakasih…
Sangat membantu dalam menyelesaikan tugas saya
terimakasih :) sangat membantu saya dalam memahami persamaan kuadrat
Dak tau
Terima kasih. Sangat membantu
Gk guna
Ko gtu sih