Kecapatan dan percepatan partikel menunjukkan seberapa cepat atau lambat laju seuatu partikel. Gerak sebuah partikel dengan persamaan jarak s memiliki kecepatan v dan percepatan a. Waktu yang dibutuhkan partikel untuk menempuh jarak sejauh s adalah t. Satuan untuk menyatakan jarak adalah meter (m) dan satuan untuk menyatakan waktu adalah sekon (s). Sementara satuan untuk menyatakan kecepatan dan percepatan partikel berturut-turut adalah m/s dan m/s2.
Kecepatan dan percepatan partikel dapat berupa gerak lurus beratuan (GLB) atau gerak lurus berubah beraturan (GLBB). Untuk sebuah gerak partikel yang dinyatakan dalam persamaan s(t), kecepatan dan percepatan partikel dapat diketahui berturut-turut melalui persamaan v(t) = s'(t) dan a(t) = s”(t).
Persamaan s(t) merupakan sebuah persamaan dengan variabel t dengan s menunjuk jarak yang ditempuh partikel dan t adalah waktu. Misalkan sebuah partikel bergerak lurus dengan persamaan s(t) = t2 ‒ 1. Artinya, jarak tempuh benda yang bergerak sampai waktu t = 3 adalah s(3) = 32 ‒ 1 = 9‒1 = 8 meter.
Dari persamaan jarak yang berbentuk s(t) juga dapat diketahui kecepatan dan percepatan partikel atau benda.

Baca Juga: Gerak Benda Jatuh Bebas dan Vertikal ke Atas
Bagaimana cara menghitung kecepatan yang ditempuh partikel dari gerak partikel dalam persamaan s(t)? Bagaimana cara menghitung percepatan yang ditempuh partikel dengan persamaan jarak s(t)? Sobat idshchool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Hubungan Persamaan Jarak S(t) dengan Kecepatan v(t)
- Hubungan Persamaan Jarak S(t) dengan Percepatan a(t)
- Contoh Penggunaan Hubungan Persamaan s(t), v(t), dan a(t)
- Contoh Soal dan Pembahasan
Hubungan Persamaan Jarak S(t) dengan Kecepatan v(t)
Partikel yang bergerak lurus berubah beraturan memiliki kecepatan yang berubah-ubah (tidak tetap). Misalnya pada partikel yang bergerak menempuh jarak s dalam waktu t. Kecepatan rata-rata partikel dapat diperoleh dengan persamaan selisih jarak (Δs) per selisih waktu (Δt).

Saat nilai selang t menuju waktu yang relatif singkat atau mendekati nol maka persamaan menjadi bentuk limit. Dari bentuk persamaan limit tersebut sama dengan definisi turunan. Misalkan fungsi jarak adalah s(t), turunan pertama dari fungsi jarak disimbolkan dengan ds(t)/dt atau s’(t).
Jadi persamaan kecepatan partikel dapat diperoleh dengan mencari turunan pertama dari fungsi jarak s(t).

Baca Juga: Perbedaan Kelajuan dan Kecepatan Rata-Rata dalam Bahasan Fisika
Hubungan Persamaan Jarak S(t) dengan Percepatan a(t)
Percepatan diperoleh dari perubahan kecepatan per selang waktu. Dengan cara yang sama seperti sebelumnya dapat diperoleh hubungan antara persamaan kecepatan dan percepatan partikel.

Hubungan tersebut dinyatakan dalam bentuk turunan pertama fungsi kecepatan terhadap waktu v(t) adalah fungsi percepatan a(t).
Diketahui bahwa persamaan kecepatan v(t) sama dengan turunan pertama fungsi jarak s(t). Sehingga dapat disimpulkan bawah fungsi percepatan a(t) adalah turunan pertama dari turunan pertama fungsi jarak. Atau persamaan percepatan partikel sama dengan turunan kedua dari fungsi jarak s(t), secara matematis dinyatakan a(t) = s”(t).

Baca Juga: Cara Menghitung Kecepatan Peluru yang Menumbuk Ayunan Balistik
Contoh Penggunaan Hubungan Persamaan s(t), v(t), dan a(t)
Sebuah partikel bergerak pada lintasan garis lurus. Persamaan partikel itu yang dirumuskan dengan s(t) = t3 + 6t2 + 9t + 4. Diketahui satuan s dalam meter dan t dalam detik atau sekon.
Jarak tempuh partikel t dapat diketahui dengan cara substitusi nilai t pada pesamaan s(t). Untuk mengetahui kecepatan dan percepatan partikel dapat dihitung melalui persamaan kecepatan v(t) dan percepatan a(t). Persamaan untuk kecepatan dan percepatan partikel adalah turunan pertama dan kedua dari persamaan jarak.
Soal:
Diketahui persamaan partikel adalah s(t) = t3 + 6t2 + 9t + 4.
Dari persamaan tersebut dapat diketahui jarak yang telah partikel ditempuh partikel saat t. Misalkan pada saat t = 2, jarak tempuh partikel sama dengan s(2) = 23 + 6×22 + 9×2 + 4 = 8 + 24 + 18 + 4 = 54 meter.
Persamaan kecepatan dan percepatan partikel dapat dicari melalui turunan pertama dan kedua dari persamaan jarak seperti cara penyelesaian berikut.
- Persamaan kecepatan v(t) = s’(t):
v(t) = 3 × t3‒1 ‒ 2 × 6t2‒1 + 9t1‒1
= 3t2 + 12t1 + 9t0
= 3t2 + 12t + 9
- Persamaan percepatan a(t) = s’’(t):
a(t) = s’’(t)
a(t) = v’(t)
= 2×3t2‒1 + 12t1‒1
= 6t1 + 12t0 → a(t) = 6t + 12
Sedangkan nilai kecepatan dan percepatan partikel dapat diperoleh dari substitusi nilai waktu t ke persamaan kecepatan dan percepatan partikel. Misalnya pada watu t = 2 diperoleh kecepatan partikel v(2) = 45 m/s dan percepatan partikel a(2) = 24 m/s2.

Baca Juga: Kecepatan Benda Setelah Tumbukan
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Kecepatan dan Percepatan Partikel
Sebuah partikel bergerak dengan persamaan s(t) = t3 ‒ 5t2 + 5t dengan satuan meter (m). Besar percepatan partikel saat t = 2 s adalah ….
A. 2 m/s2
B. 4 m/s2
C. 6 m/s2
D. 8 m/s2
E. 10 m/s2
Pembahasan:
Dari soal diketahui persamaan jarak untuk partikel: s(t) = t3 ‒ 5t2 + 5t.
Persamaan percepatan partikel:
v(t) = s’(t) = 3t2 ‒ 2×5t + 5 = 3t2 ‒ 10t + 5
a(t) = s’’(t) = v’(t) = 6t ‒ 10 =
Menghitung besar percepatan partikel saat t = 2 s:
a(t) = 6t ‒ 10
a(2) = 6×2 ‒ 10 = 12 ‒ 10 = 2 m/s2
Besar percepatan partikel saat t = 2 s adalah 2 m/s2.
Jawaban: A
Contoh 2 – Soal Kecepatan dan Percepatan Partikel
Sebuah partikel bergerak dari kedudukan awal dengan persamaan kedudukan x = 2t2 + 5t + 3. Kecepatan rata-rata partikel darti t = 2 s sampai t = 5 s adalah ….
A. 9 m/s
B. 13 m/s
C. 19 m/s
D. 27 m/s
E. 31 m/s
Pembahasan:
Dari soal diketahui persamaan kedudukan x = 2t2 + 5t + 3
- Jarak yang ditempuh untuk t = 2 s
x = 2t2 + 5t + 3
= 2×22 + 5×2 + 3 = 8 + 10 + 3
= 21 m - Jarak yang ditempuh untuk t = 5 s
x = 2t2 + 5t + 3
= 2×52 + 5×5 + 3
= 50 + 25 + 3 = 78 m
Menghitung kecepatan rata-rata partikel darti t = 2 s sampai t = 5 s (Δt = 3 s):
v(t) = Δx/Δt
v(t) = 78 – 21/5-2
v(t) = 57/3 = 19 m/s
Jadi, kecepatan rata-rata partikel darti t = 2 s sampai t = 5 s adalah 19 m/s.
Jawaban: C
Contoh 3 – Soal Kecepatan dan Percepatan Partikel
Sebuah partikel bergerak dengan persamaan vektor posisi r = (2t2 ‒ t)i + (t3 + t)j. Besar kecepatan partikel saat t = 1 sekon adalah ….
A. 1 m/s
B. 3 m/s
C. 4 m/s
D. 5 m/s
E. 6 m/s
Pembahasan:
Diketahui persamaan gerak partikel dengan vektor posisi r = (2t2 ‒ t)i + (t3 + t)j. Persamaan kecepatan partikel tersebut dapat diperoleh dari turunan pertama vektor posisi r.

Diperoleh persamaan kecepatan partikel v(t) = (4t ‒ 1)i + (3t2 + t)j. Kecepatan partikel saat t = 1 sekon dapat diperoleh dari subsitusi nilai t = 1 ke persamaan v (t). Sehingga, kecepatan vektor saat t = 1 sekon memenuhi persamaan di bawah.
v(t) = (4t ‒ 1)i + (3t2 + t)j
v(1) = (4×1 ‒ 1)i + (3×12 + 1)j
= (4‒1)i + (3+1)j
= 3i + 4j
Diperoleh persamaan kecepatan partike saat t = 1 adalah v = 3i + 4j. Resultan vektor dapat dihitung seperti cara di bawah.
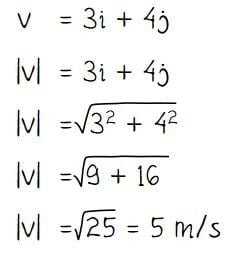
Jadi, besar kecepatan partikel saat t = 1 sekon adalah 5 m/s.
Jawaban: D
Contoh 4 – Soal Jarak yang Ditempuh Partikel
Sebuah partikel bergerak dengan kecepatan v(t) = (3t² ‒ 2t) m/s. Jika titik asal partikel berada pada O(0,0) maka posisi partikel pada saat t = 2 s adalah ….
A. 2 m
B. 4 m
C. 6 m
D. 8 m
E. 10 m
Pembahasan:
Keterangan pada soal memberikan informasi-informsi seperti berikut.
- Persamaan kecepatan gerak partikel: v(t) = 3t² ‒ 2t
- Titik asal partikel berada pada O(0,0)
Posisi partikel dapat diperoleh dari hasil integral pertama persamaan kecepatan partikel.

Menghitung posisi partikel pada saat t = 2 s:
r(t) = t3 ‒ t2
r(2) = 23 ‒ 22
r(2) = 8 ‒ 4 = 4 meter
Jadi, posisi partikel pada saat t = 2 s adalah 4 meter.
Jawaban: B
Demikianlah tadi ulasan jarak kecepatan dan percepatan partikel jika diketahui persamaan jarak s(t). Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Kecepatan Air yang Masuk Melalui pipa Venturimeter
