Rotasi berlawanan arah jarum jam merupakan bentuk tranformasi geometri yang memindahkan titik sejauh α secara memutar. Hasil transformasi titik dipengaruhi oleh letak titik pusat dan besar sudut putar. Sebagai contoh, hasil transformasi titik A(1, 2) karena rotasi pada pusat O(0, 0) sejauh α = 90o berlawanan arah jarum jam adalah (–2, 1). Sementara hasil transformasi titik A(1, 2) karena rotasi pada pusat P(1, 1) sejauh α = 90o dengan arah yang sama adalah (–2, 1).
Simbol transformasi geometri rotasi berlawanan arah jarum jam sejauh α adalah R[P; +α]. Titik P merupakan pusat rotasi, tanda + menunjukkan arah rotasi, dan nilai α menyatakan besar sudut rotasi.
Pada detail ulasan di bawah akan dibahas bagaimana cara mendapat rumus rotasi berlawanan arah jarum jam. Untuk rotasi searah jarum jam ada di halaman rumu rotasi searah jarum jam.
Daftar isi:
Baca Juga: Vektor yang Saling Tegak Lurus dan Sejajar
Rumus Rotasi Berlawanan Arah Jarum Jam
Rumus transformasi geometri rotasi dibedakan menjadi dua yaitu saat sudut putar O(0, 0) dan saat sudut putar P(a, b). Kedua rumus tersebut memiliki bentuk seperti berikut.
1) Pada Pusat O(0, 0)
Hasil transformasi titik (x, y) kerena rotasi R[O(0, 0); +αo] memenuhi persamaan matriks transformasi berikut.

Misalnya pada transformasi geometri titik A(x, y) karena rotasi [RO(0, 0); +90o] menghasilkan titik A’(–y, x). Cara mendapatkannya ditunjukkan melalui operasi persamaan matriks di bawah.
![Rotasi R[O(0, 0); +90^o]](https://idschool.net/wp-content/uploads/2021/03/Matriks-Rotasi-Pusat-O-dengan-Besar-Sudut-90-Derajat-Berlawanan-Arah-Jarum-Jam.jpg)
Sebagai contoh, hasil rotasi titik K(3, 5) pada pudat O(0, 0) sejauh 90o berlawana arah jarum jam adalah titik K’(–5, 3).

Dengan cara yang sama dapat diperoleh persamaan umum untuk mendapatkan hasil rotasi pada pusat O(0, 0) sejauh α = 30o, 45o, 60o, 180o, 270o dan besar sudut lainnya.
Tabel rumus rotasi titik (x, y) pada pusat O(0, 0) sejauh α berlawanan arah jarum jam:
| Rotasi | Hasil rotasi |
| R[O; +30o] | (1/2x√3 – 1/2y, 1/2x + 1/2y√3) |
| R[O; +45o] | (1/2x√2 – 1/2√2, 1/2x√2 + 1/2y√2) |
| R[O; +60o] | (1/2x – 1/2y√3, 1/2x√3 + 1/2y) |
| R[O; +90o] | (–y, x) |
| R[O; +180o] | (–x, –y) |
| R[O; +270o] | (y, –x) |
Baca Juga: Komposisi Transformasi Geometri dengan Matriks
2) Pada Pusat P(a, b)
Hasil transformasi titik (x, y) kerena rotasi R[P(a, b); +αo] memenuhi persamaan matriks transformasi berikut.
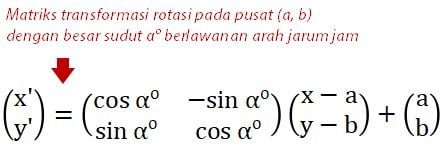
Misalnya, hasil transformasi geometri dari titik A(x, y) karena rotasi R[P(a, b); +90o] adalah itik A'(–y + a + b, x – a + b). Cara mendapatkan koordinat titik tersebut terdapat pada operasi persamaan matriks di bawah.
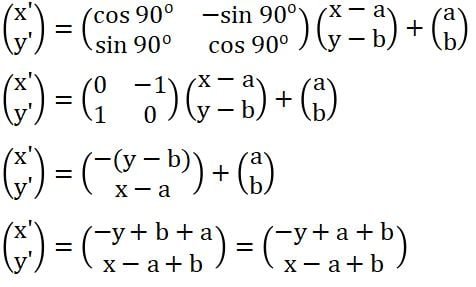
Contoh: hasil transformasi titik K(3, 5) kerena rotasi R[P(1,−2); +90o] adalah titik K’(–5 + 1 +(−2), 3 − 1 + (−2)) = K’(−6, 0).

Selanjutya, dengan cara yang sama dapat diperoleh persamaan umum untuk mendapatkan hasil rotasi pada pusat P(a, b) dengan besar sudut rotasi α = 30o, 45o, 60o, 180o, 270o dan besar sudut lainnya.
Secara ringkas, persamaan umum hasil rotasi titik pada pusat P(a, b) dengan besar sudut rotasi α = 30o, 45o, 60o, 90, 180o, dan 270o diberikan seperti tabel berikut.

Baca Juga: Transformasi Geometri (Translasi, Refleksi, Rotasi, dan Dilatasi)
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman terkait bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!
Contoh 1 – Rotasi Titik
Titik B (6, 4) dirotasikan 270° berlawanan arah jarum jam terhadap titik pusat (a, b) sehingga diperoleh titik B'(2, –8). Hasil b – 2a adalah ….
A. –2
B. 0
C. 2
D. 4
E. 6
Pembahasan:
Bayangan hasil rotasi dapat dicari menggunakan rumus yang telah diberikan di atas.
Menentukan bayangan absis (x’):
x’ = (x – a) × cos 270o – (y – b) × sin 270o + a
x’ = (6 – a) × 0 – (4 – b) × (–1) + a = 4 – b + a
Menentukan bayangan ordinat (y’):
y’ = (x – a) × sin 270o + (y – b) × cos 270o + b
y’ = (6 – a) × (–1) + (4 – b) × 0 + b = –6 + a + b
Diperoleh persamaan x’ = 4 – b + a dan y’ = –6 + a + b. Diketahui bahwa bayangan titik yang dihasilkan adalah titik B'(2, –8), sehingga dapat diperoleh dua persamaan berikut.
- 2 = 4 – b + a
a – b = 2 – 4
a – b = –2 → a = b – 2
- –8 = –6 + a + b
a + b = –8 + 6
a + b = –2
Substitusi persamaan a = b – 2 ke persamaan a + b = –2 untuk mendapatkan nilai b:
a + b = –2
b – 2 + b = –2
2b = –2 + 2 = 0
b = 0/2 = 0
Menghitung nilai a:
a = b – 2
a = 0 – 2 = –2
Nilai b – 2a = 0 – 2(–2) = 0 + 4 = 4.
Jawaban: D
Contoh 2 – Matriks transformasi

Pembahasan:
Komposisi matriks transformasi rotasi berlawanan arah jarum jam pada pusat O(0, 0) sejauh 60o yang dilanjutkan sejauh 30o memenuhi persamaan T = T2 º T1.
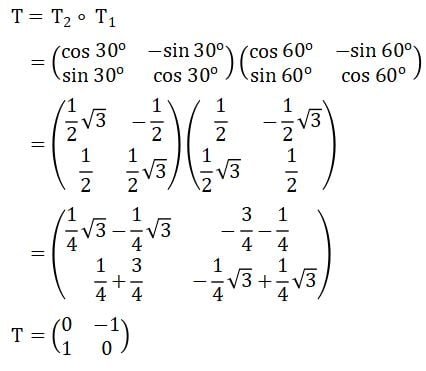
Jawaban: A
Demikianlah tadi ulasan rotasi berlawanan arah jarum jam dengan besar sudut α = 30, 45, 60, 90, 180 derajat. Terima kasih sudah mengunjungi idschool(dot)net, semoga berlanfaat!
Baca Juga: Barisan Aritmatika dan Geometri

Terima kasih , sangat membantu dlm penyelesaian soal- soal.