Rumus Aturan Sinus dan Cosinus +Contoh Penggunaannya

Rumus aturan sinus dan cosinus menyatakan hubungan antara panjang sisi-sisi segitiga dengan besar sudut segitiga. Penggunaan rumus aturan sinus dan cosinus dapat membantu banyak menyelesaikan masalah terkait panjang sisi dan besar sudut pada suatu segitiga sembarang.

Fungsi sinus dan cosinus sendiri adalah dua fungsi trigonometeri yang menyatakan perbandingan panjang sisi depan/samping dengan sisi miring. Di mana fungsi sinus sama dengan perbandingan antara sisi depan dan sisi miring. Sedangkan fungsi cosinus sama dengan perbandingan antara sisi samping dengan sisi miring.

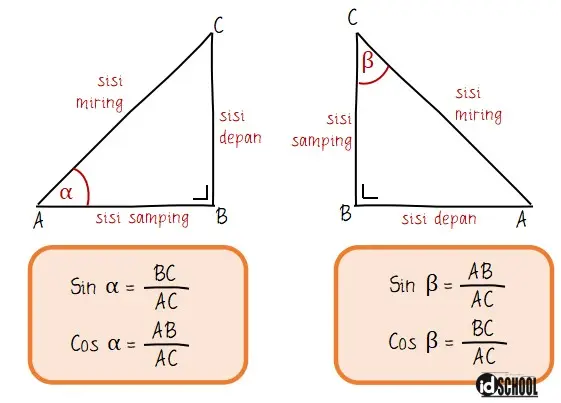
Dua persamaan di atas menunjukkan persamaan fungsi sinus dan cosinus. Sementara rumus aturan sinus dan cosinus memuat persamaan yang menghubungkan besar sudut dan panjang sisi pada suatu segitiga.

Bagaimana bentuk rumus aturan sinus dan cosinus? Sobat idschool dapat mencari tahu bahasan dan contoh penggunaan rumus aturan sinus dan cosinus pada ulasan di bawah.

Table of Contents

• Rumus Aturan Sinus
• Rumus Aturan Cosinus
• Contoh Soal dengan Penggunaan Rumus Aturan Sinus dan Cosinus
  • Contoh 1 – Cara Penggunaan Rumus Aturan Sinus
  • Contoh 2 – Cara Penggunaan Rumus Aturan Cosinus
  • Contoh 3 – Cara Penggunaan Rumus Aturan Sinus dan Cosinus

Rumus Aturan Sinus

Aturan sinus merupakan hubungan antara besar sudut dan panjang sisi yang berlwanan. Penggunaan aturan sinus biasanya terdapat pada cara menentukan panjang sisi segitiga yang telah diketahui dua besar sudutnya dan satu panjang sisi yang berhadapan dengan salah satu besar sudut yang diketahui.

Misalkan sebuah segitiga ABC memiliki tiga panjang sisi yaitu a, b, dan c satuan. Dan besar ketiga sudut segitiga ABC adalah α, β, dan γ.

Rumus aturan sinus pada segitiga ABC memenuhi persamaan berikut.

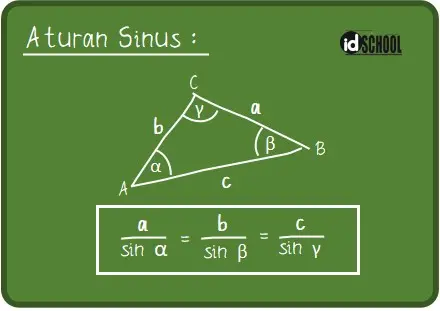
Baca Juga: Cara Menentukan Nilai Minimum/Maksimum Fungsi Trigonometri

Rumus Aturan Cosinus

Aturan cosinus dapat digunakan untuk menghitung panjang sisi atau besar sudut yang belum diketahui pada suatu segitiga.

Rumus aturan cosinus digunakan apabila pada suatu segitiga terdapat dua panjang sisi yang diketahui dan besar sebuah sudut yang diapit kedua sisi tersebut. Panjang sisi yang berhadapan dengan sudut apit dapat ditentukan panjangnya dengan aturan cosinus.

Misalkan sebuah segitiga ABC memiliki tiga panjang sisi yaitu a, b, dan c satuan. Dan besar ketiga sudut segitiga ABC adalah α, β, dan γ.

Rumus aturan cosinus pada segitiga ABC memenuhi tiga persamaan berikut.

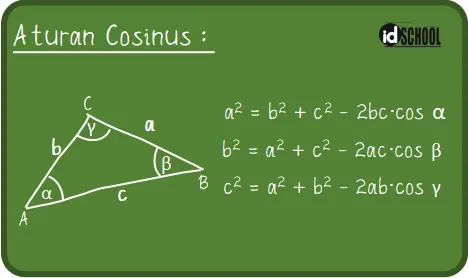
Baca Juga: Cara Menentukan Nilai Limit Fungsi Trigonomrtri untuk x Menuju Tak Hingga

Contoh Soal dengan Penggunaan Rumus Aturan Sinus dan Cosinus

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana cara penggunaan rumus aturan sinus dan cosinus. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Cara Penggunaan Rumus Aturan Sinus

Diketahui segitiga PQR, panjang sisi QR = 8 cm, ∠P = 45^o dan  ∠R = 45^o. Panjang sisi PQ adalah ….
A. 2√6 cm
B. 4√2 cm
C. 4√6 cm
D. 8√3 cm
E. 8√6 cm

Pembahasan:
Dari keterangan yang diberikan pada soal dapat diperoleh informasi seperti yang termuat dalam gambar di bawah.

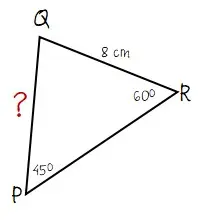
Ada dua besat sudut segitiga PQR dan satu panjang sisi segitiga yang diketahui. Panjang sisi segitiga lainnya yang belum diketahui dapat dihitung menggunakan aturan sinus seperti cara berikut.

Jadi, panjang sisi PQ = 4√6 cm.

Jawaban: C

Contoh 2 – Cara Penggunaan Rumus Aturan Cosinus

Dua kapal A dan B meninggalkan pelabuhan P bersama-sama. Kapal A berlayar dengan arah 30^o dan kecepatan 30 km/jam, sedangkan kapal B berlayar dengan arah 90^o dan kecepatan 45 km/jam. Jika kedua kapal berlayar selama 2 jam, maka jarak kedua kapal tersebut adalah ….
A. 30√2 km
B. 30√5 km
C. 30√7 km
D. 30√10 km
E. 30√13 km

Pembahasan:
Dari keterangan pada soal dapat diperoleh informasi bahwa kecepatan kapal A adalah v_A = 30 km/jam dan kecepatan kapal B adalah v_B = 45 km/jam.

Diketahui bahwa kedua kapal telah berlayar selama t = 2 jam. Sehingga jarak yang ditempuh kedua kapal dapat dihitung seperti cara berikut.

• Jarak yang ditempuh kapal A (S_A):
  S_A = v_A × t
  S_A = 30 × 2 = 60 km

• Jarak yang ditempuh kapal B (S_B):
  S_B = v_B × t
  S_B = 45 × 2 = 90 km

Kapal A bergerak pada arah 30^o dan kapal B bergerak pada arah 90^o dari pelabuhan. Gambar yang sesuai dengan kondisi pernyataan-pernyataan pada soal ditunjukkan seperti berikut.

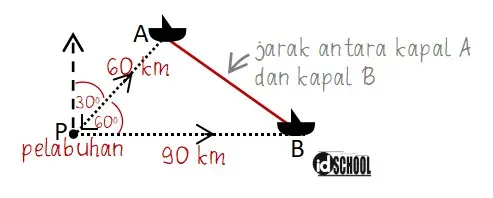
Menghitung jarak antara kapal A dan kapal B:
AB² = PA² + PB² ‒ 2×PA×PB×cos ∠APB
AB² = 60² + 90² ‒ 2×60×90×cos 60^o
AB² = 3.600 + 8.100 ‒ 2× 5.400×½
AB² = 3.600 + 8.100 ‒ 5.400 = 6.300
AB =  √6.300 = √(900×6)
AB = √900 × √7 = 30√7 km

Jadi, jarak terdekat dari pelabuhan A ke C adalah 30√7 km.

Jawaban: C

Contoh 3 – Cara Penggunaan Rumus Aturan Sinus dan Cosinus

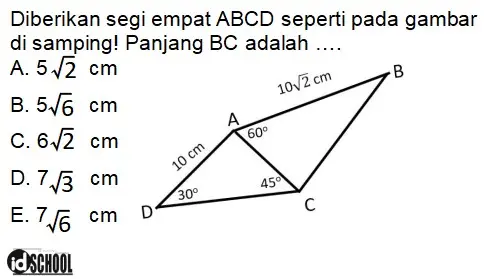
Pembahasan:
Untuk mencari panjang BC, sobat idschool perlu menghitung panjang AC terlebih dahulu.

Panjang AC dapat dihitung dengan rumus aturan sinus karena diketahui besar dua sudut dan satu panjang sisi segitiga. Sedangkan panjang BC dapat dihitung dengan rumus aturan cosinus karena diketahui satu panjang sisi dan besar dua sudut segitiga.

Menghitung panjang BC:
BC² = AC² + AB² ‒ 2×AC×AC×cos A
BC²=(5√2)²+(10√2)²‒2×5√2×10√2 × ½ 
BC² = 50 + 200 ‒ 200 × ½ 
BC² = 50 + 200 ‒ 100 = 150
BC =  √150 = √(25×6)
BC = √25 × √6 = 5√6 cm

Jadi, panjang BC = 5√6 cm.

Jawaban: D

Demikianlah tadi ulasan contoh penggunaan rumus aturan sinus dan cosinus untuk menyelesikan soal. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Fungsi Trigonometri dan Cara Menentukan Nilai Limit Fungsi Trigonometri