4 Bentuk Rumus Selisih/Jumlah Fungsi Sin dan Cos

Rumus selisih/jumlah fungsi sin dan cos adalah fungsi identitas yang dapat digunakan untuk membantu perhitungan dalam bahasan fungsi trigonometri. Ada 2 bentuk rumus selisih dari fungsi sinus dan cos, selain itu ada juga 2 bentuk rumus jumlah fungsi sin dan cos. Sehingga ada 4 bentuk rumus selisih/jumlah fungsi sin dan cos yang menjadi fungsi identitas fungsi trigonometri.

Rumus selisih/jumlah fungsi sinus dan cos dapat digunakan untuk membantu perhitungan nilai dari suatu fungsi trigonometri. Contohnya pada bukan dua sudut istimewa seperti 75^o dan 15^o. Hasil jumlah sudut 75^o dan 15^o adalah 90^o, sedangkan selisihnya adalah 60^o, di mana keduanya merupakan sudut istimewa. 4 Bentuk rumus selisih/jumlah fungsi sin dan cos sesuai dengan persamaan-persamaan di bawah.

Baca Juga: Rumus Perkalian Fungsi Sinus dan Cosinus

Meskipun rumusnya terlihat panjang dan rumit, namun ada cara yang digunakan untuk menghafal rumus-rumus tersebut. Rumus selisih/jumlah fungsi sin dan cos di atas dapat dibuktikan melalui fungsi identitas fungsi trigonometri lainnya. Bagaimana bentuk rumus selisih fungsi sin dan cos? Bagaimana bentuk rumus jumlah fungsi sin dan cos? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Rumus Jumlah Fungsi Sin
• Rumus Selisih Fungsi Sin
• Rumus Jumlah Fungsi Cos
• Rumus Selisih Fungsi Cos

Rumus Jumlah Fungsi Sin

Rumus sin jumlah: sin jumlah sama dengan dua sin setengah jumlah cos setengah selisih

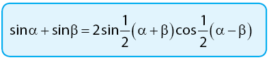
Bukti:
Pada pembahasan rumus perkalian fungsi sinus dan cosinus, sudah terbukti bahwa:
2×sin A×cos B = sin (A + B) + sin ( A ‒ B)

Misalkan: α = A + B dan β = A – B
Sehingga,
α + β = 2A → A = ¹/₂(α + β)
α – β = 2B → A = ¹/₂(α – β)

Substitusi nilai A, B, α, dan β pada rumus perkalian sinus dan cosinus, sehingga diperoleh persamaan dan penyelesaiannya seperti berikut.

sin α + sin β = 2×sin ¹/₂(α + β)×cos ¹/₂(α ‒ β)

Contoh penggunaan rumus sin jumlah:
Diketahui besar sudut α = 105^o dan β = 15^o, nilai sin α + sin β adalah ….
A. ¹/₆√2
B. ¹/₂√2
C. ¹/₆√3
D. ¹/₂√5
E. ¹/₂√6

Pembahasan:
sin α + sin β = sin 105^o + sin 15^o
sin α + sin β  = 2×sin ¹/₂(105^o + 15^o)×cos ¹/₂(105^o ‒ 15^o)
sin α + sin β  = 2×sin ¹/₂(120^o)×cos ¹/₂(90^o)
sin α + sin β  = 2×sin 60^o×cos 45^o
sin α + sin β  = 2×¹/₂√3×¹/₂√2
sin α + sin β  = ¹/₂√6

Jawaban: E

Rumus Selisih Fungsi Sin

Rumus sin selisih: sin selisih sama dengan dua cos setengah jumlah sin setengah selisih.

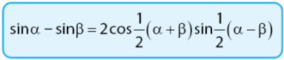
Bukti:
Pada pembahasan rumus perkalian fungsi sinus dan cosinus, sudah terbukti bahwa:
2 × cos A × sin B = sin (A + B) ‒ sin ( A ‒ B)

Misalkan: α = A + B dan β = A – B
Sehingga,
α + β = 2A → A = ¹/₂(α + β)
α – β = 2B → A = ¹/₂(α – β)

Substitusi nilai A, B, α, dan β pada rumus perkalian sinus dan cosinus, sehingga diperoleh persamaan dan penyelesaian seperti berikut.

sin α ‒ sin β = 2 × cos ¹/₂(α + β) × sin ¹/₂(α ‒ β)

Baca Juga: Rumus Trigonometri Sudut Pertengahan

Contoh penggunaan rumus sin selisih:
Diketahui besar sudut α = 105^o dan β = 15^o, nilai sin α + sin β adalah ….
A. ¹/₆√2
B. ¹/₂√2
C. ¹/₆√3
D. ¹/₂√5
E. ¹/₂√6

Pembahasan:
sin α ‒ sin β = sin 105^o ‒ sin 15^o
sin α ‒ sin β  = 2 × cos ¹/₂(105^o + 15^o) × sin ¹/₂(105^o ‒ 15^o)
sin α ‒ sin β  = 2 × cos ¹/₂(120^o) × sin ¹/₂(90^o)
sin α ‒ sin β  = 2 × cos 60^o × sin 45^o
sin α ‒ sin β  = 2 × ¹/₂ × ¹/₂√2
sin α ‒ sin β  = ¹/₂√2

Jawaban: B

Rumus Jumlah Fungsi Cos

Rumus cos jumlah: cos jumlah sama dengan dua cos setengah jumlah cos setengah selisih.

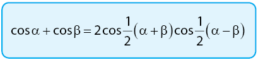
Bukti:
Pada pembahasan rumus perkalian fungsi sinus dan cosinus, sudah terbukti bahwa:
2 × cos A × cos B = cos (A + B) + cos ( A ‒ B)

Misalkan: α = A + B dan β = A – B
Sehingga,
α + β = 2A → A = ¹/₂(α + β)
α – β = 2B → A = ¹/₂(α – β)

Substitusi nilai A, B, α, dan β pada rumus perkalian sinus dan cosinus, sehingga diperoleh persamaan dan penyelesaiannya seperti berikut.

Contoh penggunaan rumus cos jumlah:
Diketahui besar sudut α = 105^o dan β = 15^o, nilai cos α + cos β adalah ….
A. ¹/₆√2
B. ¹/₂√2
C. ¹/₆√3
D. ¹/₂√5
E. ¹/₂√6

Pembahasan:
cos α + cos β = cos 105^o + cos 15^o
cos α + cos β  = 2 × cos ¹/₂(105^o + 15^o) × cos ¹/₂(105^o ‒ 15^o)
cos α + cos β  = 2 × cos ¹/₂(120^o) × cos ¹/₂(90^o)
cos α + cos β  = 2 × cos 60^o × cos 45^o
cos α + cos β  = 2 × ¹/₂ × ¹/₂√2
cos α + cos β  = ¹/₂√2

Jawaban: B

Rumus Selisih Fungsi Cos

Rumus cos selisih: cos selisih sama dengan min dua sin setengah jumlah sin setengah selisih.

Bukti:
Pada pembahasan rumus perkalian fungsi sinus dan cosinus, sudah terbukti bahwa:
‒2 × sin A × sin B = cos (A + B) ‒ cos ( A ‒ B)

Misalkan: α = A + B dan β = A – B
Sehingga,
α + β = 2A → A = ¹/₂(α + β)
α – β = 2B → A = ¹/₂(α – β)

Substitusi nilai A, B, α, dan β pada rumus perkalian sinus dan cosinus, sehingga diperoleh persamaan dan penyelesaian seperti berikut.

cos α ‒ cos β = ‒2 × sin ¹/₂(α + β) × sin ¹/₂(α ‒ β)

Contoh penggunaan rumus cos selisih:
Diketahui besar sudut α = 105^o dan β = 15^o, nilai cos α + cos β adalah ….
A. ¹/₆√2
B. ¹/₂√2
C. ¹/₆√3
D. ¹/₂√5
E. ¹/₂√6

Pembahasan:
cos α ‒ cos β = sin 105^o ‒ sin 15^o
cos α ‒ cos β  = ‒2 × sin ¹/₂(105^o + 15^o) × sin ¹/₂(105^o ‒ 15^o)
cos α ‒ cos β  = 2 × sin ¹/₂(120^o) × sin ¹/₂(90^o)
cos α ‒ cos β  = 2 × sin 60^o × sin 45^o
cos α ‒ cos β  = 2 × ¹/₂√3 × ¹/₂√2
cos α ‒ cos β  = ¹/₂√6

Jawaban: E

Sekian, pembahasan mengenai rumus selilih/jumlah fungsi sin dan cos. Terimakasih sudah berkunjung di idschool(dot)net, semoga bermanfaat!

Baca Juga: Menyelesaikan Persamaan Trigonometri