Salah satu pembahasan pada materi trigonometri adalah menyelesaikan persamaan trigonometri. Biasanya, soal yang diberikan pada persamaan trigonometri adalah untuk menentukan himpunan penyelesaian yang terdiri atas sudut-sudut yang memenuhi persamaan trigonometri. Sebagaimana yang sobat idschool ketahui bahwa bentuk grafik fungsi trigonometri bersifat periodik. Bentuknya akan berulang sama pada rentang tertentu. Sehingga, nilai fungsi trigonometri dari sebuah persamaan tidak hanya memiliki nilai tunggal.
Misalkan pada fungsi Sin x = ½, nilai x yang memenuhi tidak hanya 30o sebagaimana yang diketahui bahwa nilai Sin 30o = ½. Selain besar sudut 30o yang dapat memenuhi persamaan Sin x = ½, ada nilai lain yang dapat memenuhi persamaan tersebut. Salah satu nilai, selain x = 30o, yang dapat memenuhi persamaan Sin x = ½ adalah x = 150o.
Melalui halaman ini, sobat idschool dapat mempelajari cara menyelesaikan persamaan trigonometri dan menentukan semua himpunan penyelesaian yang memenuhi syarat yang diberikan pada soal.
Table of Contents
- Bentuk Persamaan Trigonometri Fungsi Sinus
- Bentuk Persamaan Trigonometri Fungsi Cosinus
- Bentuk Persamaan Trigonometri Fungsi Tangen
- Contoh Soal dan Pembahasan
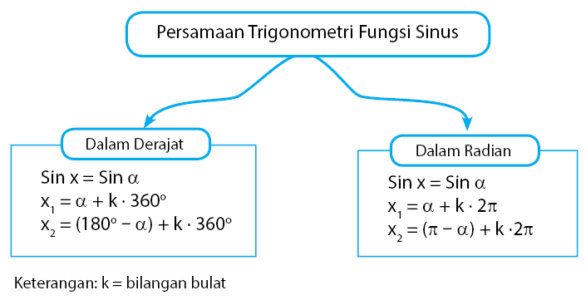
Bentuk Persamaan Trigonometri Fungsi Sinus
Grafik fungsi sinus bersifat periodik membentuk bukit dan lembah yang saling terhubung satu sama lain. Oleh sebab itu, nilai fungsi sinus untuk satu besar sudut akan sama dengan nilai fungsi sinus untuk besar sudut lain. Misalkan nilai fungsi Sin 45o yang sama nilainya dengan nilai fungsi Sin 135o yaitu ½√2. Kondisi ini dikarenakan nilai sinus dalam satu periode bersifat periodik. Nilai tertinggi fungsi y = sin x adalah 1, sedangkan nilai terendah fungsi y = sin x adalah –1.
Secara umum, persamaan trigonometri untuk fungsi sinus diberikan seperti persamaan di bawah.
Contoh soal menyelesaikan persamaan trigonometri untuk fungsi sinus.
Soal:
Tentukan himpunan penyelesaian yang memenuhi persamaan 2 Sin (2x – 60o) – √3 = 0, 0 ≤ x ≤ 360o
Pembahasan:
Menyelesaikan persamaan:
2 Sin (2x – 60o) – √3 = 0
2 Sin (2x – 60o) = √3
Sin ( 2x – 60o) = ½√3
Berdasarkan hasil persamaan akhir yang diperoleh di atas, maka dapat ditentukan himpunan penyelesaiannya.
2x – 60o = 60o + k ⋅ 360o
2x = 60o + 60o + k ⋅ 360o
2x = 120o + k ⋅ 360o
x = 60o + k⋅180o
Dan
2x – 60o = (180o – 60o) + k ⋅ 360o
2x – 60o = 120 + k ⋅ 360o
2x = 120o + 60o + k ⋅ 360o
2x = 180o + k ⋅ 360o
x = 90o + k ⋅ 180o
Diperoleh dua persamaan akhir yaitu x = 60o + k⋅180 atau x = 90o + k ⋅ 180o.
Selanjutnya, akan diselidiki pada beberapa nilai k untuk mendapatkan himpunan penyelesaiannya.
Untuk k = 0:
x = 60o + k ⋅ 180o → x = 60o
x = 90o + k ⋅ 180o → x = 90o
Untuk k = 1
x = 60o + k⋅180o → x = 240o
x = 90o + k⋅180o → x = 270o
Untuk nilai k = 2 dan lebih akan menghasilkan nilai x yang lebih dari 240o, sehingga perhitungan dicukupkan sampai nilia k = 1. Jadi, himpunan penyelesaian yang diperoleh adalah {60o, 90o, 240o, 270o}.
Baca Juga: Limit Fungsi Trigonometri
Bentuk Persamaan Trigonometri Fungsi Cosinus
Grafik fungsi cosinus juga bersifat periodik, membentuk bukit dan lembah. Pada satu periode pada fungsi y = cos x dimulai dari 1 (satu) dan kembali ke 1 (satu). Nilai tertinggi fungsi y = Cos x adalah 1 dan nilai terendah dari fungsi y = cos x adalah –1.
Nilai fungsi cosinus untuk satu besar sudut akan sama dengan nilai fungsi cosinus untuk besar sudut lain. Misalkan nilai fungsi Cos 60o yang sama nilainya dengan nilai fungsi Cos 300o, yaitu ½.
Secara umum, persamaan trigonometri untuk fungsi cosinus diberikan seperti persamaan di bawah.

Contoh soal menyelesaikan persamaan trigonometri untuk fungsi cosinus.
Soal:
Tentukan himpunan penyelesaian dari persamaan 2 Cos x – √3 = 0, 0 ≤ x ≤ 360o.
Pembahasan:
Menyelesaikan persamaan:
2 Cos x – √3 = 0
2 Cos x = √3
Cos x = ½√3
Cos x = Cos 30o
Berdasarkan rumus umum persamaan trigonometri untuk fungsi cosinus diperoleh dua persamaan berikut.
x1 = 30o + k ⋅ 360o
x2 = 150o + k ⋅ 360o
Selanjutnya, akan diselidiki untuk beberapa nilai k.
Untuk k = 0:
x1 = 30o + k ⋅ 360o → x1 = 30o
x2 = 150o + k ⋅ 360o → x2 = 150o
Untuk nilai k = 1 atau lebih akan menghasilkan nilai x yang melebihi rentang yang diberikan. Sehingga, perhitungan sampai di sini. Dan diperoleh himpunan penyelesaian yang di cari, yaitu {30o, 150o}.
Baca Juga: Integral Fungsi Trigonometri
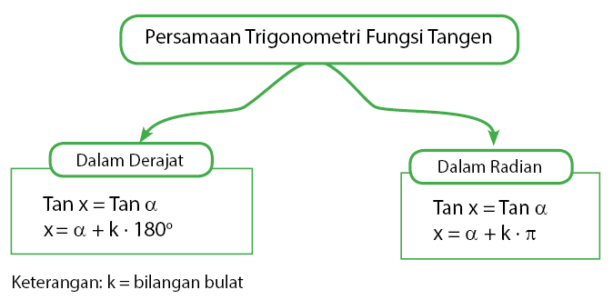
Bentuk Persamaan Trigonometri Fungsi Tangen
Grafik fungsi tangen berbeda dengan grafik fungsi sinus dan cosinus, grafiknya tidak membentuk bukit dan lembah. Hal ini dikarenakan nilai tangen yang tidak terdefinisi pada besar sudut 90o dan 270o. Sehingga, dalam rentang 0o sampai 360o terdapat dua buah asimtot. Sama seperti fungsi sinus dan cosinus, nilai tertinggi fungsi y = tan x adalah 1 dan nilai terendahnya adalah –1.
Secara umum, persamaan trigonometri untuk fungsi cosinus diberikan seperti persamaan di bawah.
Contoh soal menyelesaikan persamaan trigonometri untuk fungsi tangen.
Soal:
Tentukan himpunan penyelesaian dari persamaan tan ( 60 – ½x) = Cot (x +120o), 0 ≤ x ≤ 360o.
Pembahasan:
Menyelesaikan persamaan:
Tan (60o – ½x) = Cot ( x + 120o)
Tan (60o – ½x) = Tan (90o – ( x + 120o)
Tan (60o – ½x) = Tan (90o – x – 120o)
Tan (60o – ½x) = Tan (– x – 30o)
(60o – ½x) = (– x – 30o) + k⋅180o
x – ½x = –30o – 60o + k⋅180o
½x = –90o + k⋅180o
x = 2(–90o + k⋅180o)
x = –180o + k⋅360o
Selanjutnya akan ditentukan nilai x yang memenuhi untuk beberapa nilai k.
Untuk k = 0:
x = –180o + k⋅360o → x = –180o
(Nilai x dari hasil perhitungan di atas tidak memenuhi karena di luar rentang yang diberikan).
Selanjutnya, akan diselidiki untuk nilai k = 1,
x = –180o + k⋅360o → x = 180o (memenuhi)
Untuk nilai k = 2 atau lebih, akan menghasilkan nilai x yang berada di luar rentang. Sehingga hanya terdapat satu himpunan penyelesaian untuk x yaitu 180o.
Baca Juga: Rumus Trigonometri Sudut Pertengahan
Contoh Soal dan Pembahasan
Selain contoh soal menyelesaikan persamaan trigonometri yang telah diberikan di atas, terdapat variasi soal pengembangan dengan identitas trigonometri dan materi lain, misalnya persamaan fungsi kuadrat. Variasi contoh soal tersebut dapat dilihat pada kumpulan beberapa contoh soal menyelesaikan persamaan trigonometri yang diberikan di bawah.
Contoh 1 – Persamaan Trigonometri
Diketahui: Sin α + Cos α = ⅓, 0o ≤ α ≤ 180o. Maka nilai Sin α – Cos α adalah ….
A. 1/4√17
B. 1/3√17
C. 1/2√17
D. 2/3√17
E. √17
Pembahasan:
Menentukan nilai 2 Sin α Cos α:
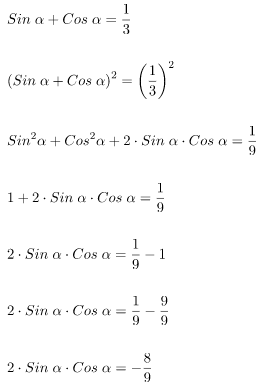
Menghitung nilai Sin α – Cos α:
(Sin α – Cos α)2 = Sin2α + Cos2α – 2 Sin α Cos α
(Sin α – Cos α)2 = 1 – 2 Sin α Cos α
(Sin α – Cos α)2 = 1 – (–8/9)
(Sin α – Cos α)2 = 1 + 8/9
(Sin α – Cos α)2 = 9/9 + 8/9 = 17/9
Sin α – Cos α = √(17/9)
Menyederhanakan nilai Sin α – Cos α:
Sin α – Cos α = √(17/9)
Sin α – Cos α = √17/√9
Sin α – Cos α = √17/3
Sin α – Cos α = 1/3 √17
Jadi, nilai Sin α – Cos α adalah 1/3√17.
Jawaban: B
Contoh 2 – Persamaan Trigonometri
Himpunan penyelesaian dari Cos 2x + 7 Sin x – 4 = 0 dengan 0o ≤ x ≤ 360o adalah ….
A. 30o dan150 o
B. 30o dan 135 o
C. 45o dan 150 o
D. 60o dan 150 o
E. 60o dan 135 o
Pembahasan:
Menyederhanakan persamaan:
Cos 2x + 7 Sin x – 4 = 0
1 – 2 Sin2x + 7 sin x – 4 = 0
– 2 Sin2x + 7 sin x – 3 = 0
Misalkan: p = sin x, maka
–2p2 + 7 p – 3 = 0
(2p – 1)( –p + 3) = 0
p = ½ atau p = –3
Untuk p = ½:
Sin x = ½ → x = 30o, 150o
Untuk p = –3 tidak ada nilai x yang memenuhi karena maksimal nilai pada fungsi trigonometri adalah 1 atau –1.
Sehingga, nilai x yang memenuhi adalah 30o dan 150o.
Jawaban: A
Contoh 3 – Persamaan Trigonometri
Himpunan penyelesaian persamaan trigonometri – √3 Cos x + Sin x = √2, 0o < x < 360o adalah ….
A. {135o, 215o}
B. {105o, 215o}
C. {105o, 195o}
D. {135o, 195o}
E. {105o, 135o}
Pembahasan:
Ubah persamaan menjadi bentuk a Cos x + b Sin x = k Cos ( x – α)
Menentukan nilai k:
k2 = a2 + b2
k2 = (–√3)2 + 12
k2 = 3 + 1 = 4
k = √4 = 2
Menentukan nilai α:
α = arc(tan b/a)
α = arc(tan –1/√3) = 150o
Sehingga,
– √3 Cos x + Sin x = √2
2 Cos ( x – 150o) = √2
Cos ( x –150o) = ½√2
Diperoleh:
x –150o = 45o + k⋅360o
x = 195o + k⋅360o
atau
x –150o = – 45o + k⋅360o
x = 105o + k⋅360o
Sekarang, akan dicari nilai x untuk beberapa nilai k.
Untuk k = 0:
x = 195o + k⋅360o → x = 195o
x = 105o + k⋅360o→ x = 105o
Untuk k = 1 dan seterusnya akan menghasilkan nilai di atas 360o. Nilainya tidak dicari karena tidak termasuk dalam himpunan penyelesaian.
Jadi, Himpunan penyelesaiannya adalah {105o, 195o}.
Jawaban: C
Sekian pembahasan mengenai cara menyelesaikan persamaan trigonometri. Secara ringkas, cara menyelesaikan persamaan trigonometri untuk menentukan besar semua sudut yang memenuhi dapat dilihat melalui tabel di bawah.

Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Aturan Cosinus (Materi dan Contoh Soal + Pembahasan)

Terimakasih sudah berbagi ilmunya