Standar deviasi biasanya dituliskan dengan Std Dev atau SD dikenal juga dengan sebutan simpangan baku. Nilai simpangan baku memberikan informasi bagaimana penyebaran nilai-nilai dalam suatu himpunan data (datasets). Nilai simpangan baku diperoleh dari perhitungan menggunakan rumus standar deviasi.
Hasil perhitungan dari penggunaan rumus standar deviasi akan menghasilkan suatu nilai. Semakin besar nilai menunjukkan bahwa data semakin tersebar jauh dari rata-rata. Semakin kecil nilai standar deviasi menunjukkan bahwa penyebaran data berada dekat di sekitar rata-rata.
Nilai hasil perhitungan standar deviasi digunakan untuk menganalisis atau menyimpulkan distribusi nilai dari dataset. Sebagai contoh, diketahui rata-rata pendapatan masyarakat Indonesia adalah 2,5 juta dengan nilai standar deviasi 500 ribu. Nilai simpangan baku tersebut cukup besar yang menunjukkan bahwa setiap penduduk tidak cukup pasti memiliki pendapatan 2,5 juta. Kondisi ini disebabkan banyaknya variansi nilai pendapatan masyarakat Indonesia.
Ada dua bentuk rumus standar deviasi yaitu rumus standar deviasi untuk data tunggal dan rumus standar deviasi untuk data kelompok. Bagaimana cara menghitung standar deviasi untuk data tunggal? Bagaimana cara menghitung standar deviasi untuk data kelompok? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Rumus Standar Deviasi Data Tunggal
Data tunggal adalah kumpulan beberapa datum yang nilainya disajikan sendiri-sendiri. Contoh data tunggal adalah 8; 11; 8; 9; 9; 10; 12; 7; 11; 9; 12; 10; 6; 8; dan 9. Contoh lain dari data tunggal adalah 85; 90; 86; 78; 88; dan 80.
Data tunggal dapat diberikan dengan cara mendaftarnya seperti pada contoh 8; 11; 8; 9; 9; 10; 12; 7; 11; 9; 12; 10; 6; 8; dan 9. Data tunggal juga dapat disajikan dalam bentuk tabel. Contoh penyajian data tunggal dalam tabel ditunjukkan seperti bentuk berikut.
| Nilai | Frekuensi |
| 6 | 1 |
| 7 | 1 |
| 8 | 3 |
| 9 | 4 |
| 10 | 2 |
| 11 | 2 |
| 12 | 2 |
Rumus standar deviasi dibedakan menjadi dua yaitu untuk data populasi dan sampel. Dua bentuk rumus standar deviasi data tunggal terdapat pada persamaan berikut.
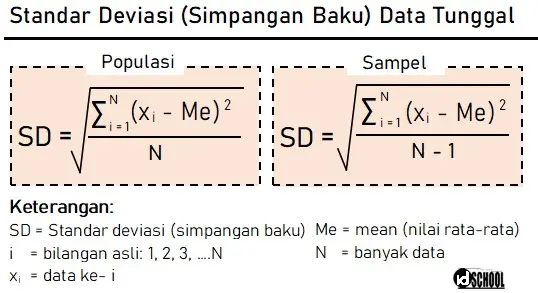
Contoh penggunaan rumus standar deviasi untuk data tunggal terdapat pada pengerjaan soal berikut.
Soal:
Tentukan simpangan baku dari data populasi: 85, 90, 86, 78, 88, dan 80!
Penyelesaian:
Pertama perlu dihitung mean (Me) atau rata-rata dari data yang diberikan seperti cara berikut.
Menghitung rata-rata:
Me = 85 + 90 + 86 + 78 + 88 + 80/6
Me = 507/6
Me = 84,5
Setelah mendapatkan nilai rata-rata, selanjutnya simpangan baku dari data populasi tersebut dapat dihitung dengan cara berikut.

Jadi, nilai standar deviasi atau simpangan baku dari data populasi 85, 90, 86, 78, 88, dan 80 adalah SD = 4,233. Nilai standar deviasi tersebut cukup kecil sehingga dapat disimpulkan bahwa data tersebar di sekitar nilai rata-rata.
Baca Juga: 4 Bentuk Rumus Variansi (Ragam)
Rumus Standar Deviasi Data Kelompok
Data kelompok adalah dataset yang diberikan dalam bentuk kelas-kelas dengan panjang kelas yang sama untuk setiap kelasnya. Pada setiap kelas terdapat informasi frekuensi yang disimbolkan dengan fi. Penyajian data kelompok biasanya diberikan dalam bentuk tabel distribusi frekuensi berdasarkan Aturan Sturges.
Simpangan baku dari data kelompok dapat dihitung menggunakan rumus standar deviasi data kelompok seperti berikut.
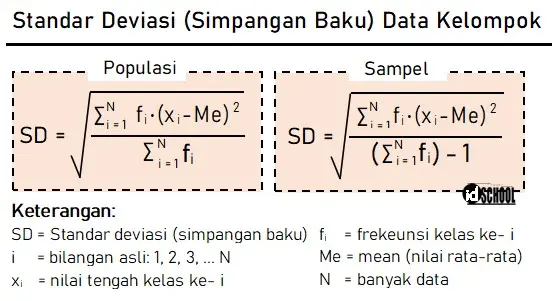
Contoh penggunaan rumus standar deviasi untuk data tunggal terdapat pada pengerjaan soal berikut.
Soal:
Tentukan simpangan baku dari data populasi yang terdapat dalam tabel di bawah.
| Nilai | Frekuensi |
| 1 ‒ 5 | 3 |
| 6 ‒ 10 | 15 |
| 11 ‒ 15 | 12 |
| 16 ‒ 20 | 8 |
| 21 ‒ 25 | 2 |
Penyelesaian:
Pertama perlu dihitung mean (Me) atau rata-rata dari data yang diberikan seperti cara berikut. Data yang diberikan dalam bentuk data kelompok, sehingga nilai rata-rata dicari dengan rumus mean data kelompok.

Diperoleh nilai rata-rata atau mean untuk data kelompok pada soal sama dengan Me = 11,875. Nilai Me tersebut digunakan untuk perhitungan nilai simpangan baku. Penggunaan rumus standar deviasi data kelompok terdapat seperti pada langkah pengerjaan berikut.

Jadi, nilai standar deviasi atau simpangan baku dari data kelompok tersebut adalah SD =5,061. Nilai standar deviasi menunjukkan bahwa dataset tersebar cukup dekat dengan rata-rata.
Baca Juga: Simpangan Rata-Rata, Ragam, dan Simpangan Baku
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana cara menghitung standar deviasai atau simpangan baku. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Cara Menghitung Standar Deviasi (Simpangan Baku) Data Tunggal
Perhatikan tabel berikut!
| Nilai | 3 | 4 | 5 | 7 | 8 |
| Frekuensi | 5 | 3 | 5 | 2 | 3 |
Simpangan baku dari data pada tabel di atas adalah ….
A. ½√29
B. ½√22
C. ½√85
D. ⅓√29
E. ⅓√85
Pembahasan:
Data pada soal di atas merupakan data tunggal sehingga simpangan baku dihitung dengan rumus standar deviasi data tunggal. Langkah perhitungan pertama yang perlu dilakukan adalah menghitung nilai mean (rataa-rata).
Menghitung rata-rata (Mean):
Me = 3×5+4×3+5×5+7×2+8×3/5+3+4+2+3
Me = 15+12+25+14+24/5+3+5+2+3
Me = 90/18 = 5
Cara menghitung simpangan baku atau standar deviasi untuk data tunggal dilakukan seperti penyelesaian berikut.

Jadi, simpangan baku dari data pada tabel di atas adalah ⅓√29.
Jawaban: D
Contoh 2 – Cara Menghitung Standar Deviasi (Simpangan Baku) Data Kelompok
Perhatikan tabel di bawah ini!
| Nilai | Frekuensi |
| 43 ‒ 47 | 5 |
| 48 ‒ 52 | 12 |
| 52 ‒ 57 | 9 |
| 58 ‒ 62 | 4 |
Simpangan baku dari data di atas adalah ….
A. √21/5
B. √29/5
C. √21
D. √23
E. √29
Pembahasan:
Data pada soal diberikan dalam bentuk tabel data kelompok. Sehingga simpangan baku dari data dapat diperoleh dengan rumus standar deviasi untuk data kelompok.
Sebelum menghitung nilai simpangan baku, nilai mean dari data kelompok tersebut perlu ditentukan terlebih dahulu. Nilai maen data kelompok dapat dihitung dengan rumus mean data kelompok. Cara mencari nilai mean data kelompok dengan menghitung jumlah perkalian nilai tengah setiap kelas dengan frekuensi setiap kelas, kemudian dibagi jumlah frekuensi.
Nilai mean data kelompok yang diperoleh selanjutnya digunakan untuk menghitung nilai simpangan baku. Penggunaan rumus standar deviasi untuk data kelompok ditunjukkan seperti yang terdapat pada langkah penyelesaian berikut.

Jadi, simpangan baku dari data di atas adalah √21.
Jawaban: C
Demikianlah tadi ulasan mengenai rumus standar deviasi dan bagaimana cara menggunakannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
