Dua postulat Einstein memunculkan rumus teori relativitas khusus mengenai besaran-besaran Fisika seperti kecepatan, waktu, panjang, dan massa yang memiliki sifat relatif. Postulat menurut KBBI dinyatakan sebagai asumsi yang menjadi pangkal dalil yang dianggap benar tanpa perlu membuktikannya; anggapan dasar; aksioma.
Sebelumnya, empat besaran tersebut (kecepatan, waktu, panjang dan massa) dinyatakan sebagai besaran-besaran yang bersifat mutlak. Ketika kecepatan gerak benda mendekati kecepatan cahaya maka muncul pertanyaan bahwa keempat besaran memiliki sifat relatif.
Postulat pertama Einstein menyatakan bahwa hukum-hukum fisika memiliki bentuk yang sama pada semua kerangka inersial. Sementara postulat Einstein kedua menyatakan bahwa cahaya yang merambat di ruang hampa dengan kecepatan tetap c tidak bergantung pada kecepatan sumber atau pengamat.
Dari postulat kedua yang diajukan Einstein timbul implikasi yang membuat besaran-besaran fisika seperti kecepatan, panjang, massa, dan waktu bersifat relatif. Relativitas atau kenisbian menunjuk suatu sifat yang tidak mutlak. Teori relativitas menjelaskan bahwa gelombang elektromagnetik tidak sesuai dengan teori gerak Newton.
Ada dua macam teori relativitas yang disampaikan Einstein yaitu teori relativitas umum dan khusus. Relativitas umum memuat teori geometri mengenai gravitasi. Sementara teori relativitas khusus menerangkan bagaimana hubungan relatif dari kecapatan, panjang, waktu, dan massa.
Bagaimana penjelasan dari setiap empat teori relativitas khusus? Apa saja rumus teori relativitas khusus yang disampaikan Einstein? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Baca Juga: Perbedaan Kelajuan dan Kecepatan Rata-Rata sebagai Besaran Fisika
4 Rumus Teori Relativitas Khusus
Kecepatan cahaya c diketahui sebagai cepat rambat gelombang yang paling tinggi dengan nilai c = 3×108 m/s. Benda yang bergerak dengan kecepatan mendekati kecepatan cahaya akan memiliki besaran-besaran yang bersifat relatif. Besaran-besaran yang terpengaruh antara lain adalah kecepatan, selang waktu, panjang, dan massa. Sehingga ada empat teori relativitas khusus yang terdapat pada teori relativitas Einstein berdasarkan dua postulat yang disampaikannya.
Keempat rumus teori relativitas khusus akibat dari postulat Einstein dijelaskan lebih banyak melalui ulasan di bawah.
1) Relativitas Kecepatan
Perhatika sebuah pesawat angkasa bergerak dengan kecepatan v1 dari Bumi dan menembakkan peluru dengan kecepatan v21. Dalam kasus ini, Bumi menjadi acuan diam bagi pesawat. Sementara pesawat angkasa yang bergerak menjadi kerangka acuan bergerak untuk peluru kendali. Seorang pengamat di Bumi mengati gerak peluru kendali tersebut memiliki kecepatan v2.
Ketika gerak benda mendekati kecepatan cahaya maka hubungan kecepatan pengamat bergerak (v1), kecepatan benda oleh pengamat diam (v2), dan kecepatan benda oleh pengamat bergerak (v21) sesuai dengan rumus teori relativitas khusus untuk kecepatan berikut.
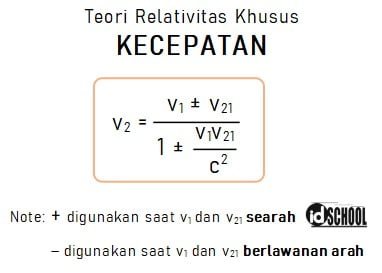
Keterangan:
v1 = kecepatan pengamat bergerak (m/s)
v2 = kecepatan benda oleh pengamat diam (m/s)
v21 = kecepatan benda oleh pengamat bergerak (m/s)
c = kecepatan cahaya (m/s)
2) Pemuluran Waktu
Einstein menerangkan bahwa selang waktu yang terukur oleh pengamat yang diam tidak sama dengan selang waktu oleh pengamat bergerak dengan kelajuan konstan. Pernyataan tersebut terjadi karena berdasarkan postulatnya, waktu bukanlah suatu besaran yang mutlak. Di mana, waktu yang terukur oleh pengamat yang bergerak terhadap kejadian lebih lama (mulur) dibanding waktu yang terukur oleh pengamat yang diam.
Rumus teori relativitas khusus yang menyatakan Hubungan antara waktu yang terukur oleh pengamat diam (Δt0) atau waktu benar (proper time) dengan waktu yang terukur oleh pengamat yang bergerak (Δt) sesuai persamaan berikut.

Baca Juga: Cepat Rambat Gelombang yang Merambat pada Tali
3) Penyusutan Panjang
Panjang juga menjadi besaran yang bersifat relatif bergantung pada kerangka acuan menurut teori yang disampaikan Einstein. Di mana panjang terukur oleh pengamat yang bergerak lebih pendek dari panjang sebenarnya.
Perhatikan sebuah pesawat yang melaju dengan kelajuan v dari titik A menuju titik B. Jarak titik A ke titik B sama dengan panjang sebenarnya (proper length) yaitu Lo. Sementara, pilot mengamati bahwa jarak AB adalah L = v·Δt0, di mana Δt0 adalah selang waktu yang dibutuhkan pesawat untuk menempuh jarak AB.
Selanjutnya dapat diperoleh perbandingan antara L dan L0 sebanding dengan Δt0 dan Δt. Sehingga dapat diperoleh rumus teori relativitas khusus untuk hubungan antara panjang terukur oleh pengamat yang diam (L0) dan panjang yang terukur oleh pengamat yang bergerak (L) seperti berikut.

Persamaan penyusutan panjang di atas hanya berlaku jika arah gerak benda relatif terhadap pengamat sejajar dengan panjang benda. Sementara panjang benda yang arah geraknya tegak lurus panjangnya tidak memeuni persamaan panyusutan panjang di atas.
4) Massa Relativistik
Besaran lain yang ikut terpengaruh karena postulat Einstein adalah massa benda. Sebelumnya, besaran massa merupakan besaran yang diangaap tetap. Setelah muncul teori relativitas Einstein, massa menjadi besaran yang memiliki sifat relatif.
Rumus teori relativitas khusus untuk massa benda (m0) yang bergerak dengan kecepatan v akan mengalami perubahan sesuai persamaan berikut.
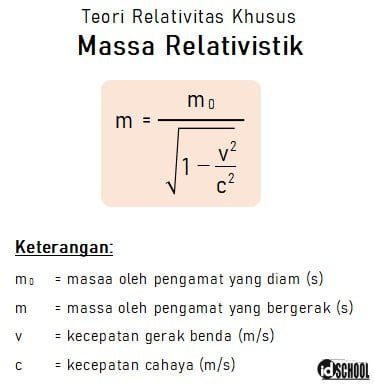
Baca Juga: Percepatan Benda yang Ditarik oleh Gaya F dan Bergerak Sejauh s pada Bidang Datar
Contoh Soal dan Pembahasan
Beberapa contoh di bawah dapat sobat idschool gunakan untuk mengukur seberapa banyak pemahaman materi. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan cara penggunaan rumus teori relativitas khusus Einstein. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlaith!
Contoh 1 – Penggunaan Rumus Teori Relativitas Khusus
Massa suatu benda yang bergerak menurut pengamat yang diam di Bumi bertambah 25% dari massa diamnya. Bila c = kelajuan cahaya dalam ruang hampa maka kecepatan gerak benda tersebut adalah ….
A. 0,3c
B. 0,4c
C. 0,6c
D. 0,8c
E. 1,25C
Pembahasan:
Dari informasi yang diberikan pada soal dapat diperoleh beberapa informasi seperti berikut.
- Massa benda diam = m0
- Massa benda bergerak:
m = m0 + 25%m0
m = 125%m0 - Kelajuan cahaya = c
Menentukan kecepatan gerak benda:

Jadi, kecepatan gerak benda tersebut adalah 0,6c.
Jawaban: C
Contoh 2 – Penggunaan Rumus Teori Relativitas Khusus
Seorang astronaut sedang menuju sebuah planet dengan menggunakan pesawat ulang alik dengan kecepatan 0,8 kali kecepatan cahaya. Dengan menggunakan transformasi Lorentz, persentase pertambahan massa astronaut tersebut adalah ….
A. 25%
B. 28%
C. 33%
D. 50%
E. 66%
Pembahasan:
Misalkan massa relativistik adalah m dan massa benda diam adalah m0 maka menurut teori relaitivtas khusus dipenuhi persamaan berikut beserta cara penyelesaiannya berikut.

Diperoleh hasil m = 10/6 m0, sehingga dapat diketahui bahwa pertambahan massa bedan sama dengan Δm = 10/6 m0 ‒ m0 = 10/6 m0 ‒ 6/6m0 = 4/6 m0 = 0,667m0. Selanjutnya, persentase pertambahan massa dapat dihitung seperti pada penyelesaian berikut.

Jadi, persentase pertambahan massa astronaut adalah 66%.
Jawaban: E
Contoh 3 – Penggunaan Rumus Teori Relativitas Khusus
Sebuah peristiwa diamati oleh seseorang yang diam berlangsung selama 8s. Jika peristiwa tersebut menurut pengamat yang bergerak terhadap peristiwa tersebut adalah 10 s, maka kecepatan (c = kecepatan cahaya) pengamat yang bergerak adalah ….
A. 0,2c
B. 0,3c
C. 0,6c
D. 0,8c
E. 0,9c
Pembahasan:
Dari informasi yang diberikan pada soal dapat diperoleh keterangan besaran dan nilanya seperti berikut.
- Selang waktu pengamatan oleh seseorang yang diam: Δt0 = 8s
- Selang waktu pengamatan oleh seseorang yang bergerak: Δt = 10
- Kecepatan cahaya = c
Menentukan kecepatan pengamat yang bergerak:
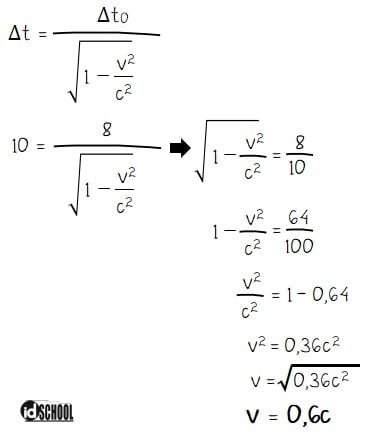
Jadi, kecepatan pengamat yang bergerak adalah 0,6c.
Jawaban: C
Demikianlah tadi ulasan rumus toeri relativitas khusus yang disampaikan Eisntein. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menghitung Kecepatan Peluru dengan Ayunan Balistik
