Turunan fungsi trigonometri adalah bentuk persamaan fungsi trigonometri yang mengalami proses metamatis operasi turunan. Simbol turunan pertama dari fungsi y terhadap x dinyatakan dalam dy/dx atau biasanya lebih sering menggunakan tanda -petik satu- (y’). Diketahui bahwa ada tiga fungsi trigonometri dasar yaitu sinus (y = sin x), cosinus (y = cos x); dan tangen (y = tan x). Turunan fungsi trigonometri untuk ketiga fungsi tersebut berturut-turut adalah y’ = cos x; y’ = ‒sin x; dan y’ = cot x
Hasil turunan fungsi trigonometri diperoleh dari definisi umum turunan yang menyatakan nilai limit pada suatu titik. Bagaimana penggunaan definisi turunan untuk mendapatkan turunan pertama fungsi trigonometri? Bagaimana cara menentukan turunan fungsi trigonometri? Sobat idschool dapat mencari tahu caranya melalui ulasan dibawah.
Table of Contents
Baca Juga: Materi Dasar Turunan Fungsi dan Teorema/Aturan Penting di Dalamnya
Definisi Turunan
Turunan suatu fungsi berawal dari sebuah permasalahan yang berkaitan dengan garis singgung. Nilai turunan didekati dengan konsep limit untuk suatu selang nilai mendekati nol. Definisi turunan pertama suatu fungsi f(x) adalah fungsi lain f’(x) (dibaca: f aksen) yang nilainya pada sebarang bilangan c adalah f’(c). Definisi turunan tersebut secara matematis dapat dituliskan melalui persamaan berikut.

Dari definisi turunan tersebut dapat digunakan untuk menentukan turunan berbagai fungsi, termasuk fungsi trigonometri.
Contoh Cara Mendapatkan Turunan Fungsi Trigonometri
Sebagai contoh, diketahui fungsi f(x) = sin x memiliki hasil turunan fungsi trigonometri f'(x) = cos x. Turunan pertama fungsi f(x) tersebut dapat diperoleh dengan cara substitusi f(x) = sin x dan f(x+h) = sin (x+h) pada definisi turunan. Dengan mengambil nilai limit h mendekati 0 (h→0) maka akan diperoleh hasil turunan fungsi f(x) = sin x.
Cara mendapatkan hasil turunan fungsi trigonometri f(x) = sin x terdapat pada penyelesaian cara berikut.
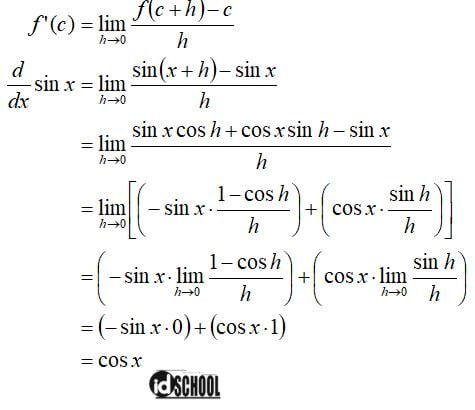
Baca Juga: Cara Menentukan Nilai Limit Suatu Fungsi Trigonometri
Hasil akhir dari proses tersebut menunjukkan bahwa turunan f(x) = sin x adalah f’(x) = cos x. Dengan cara yang sama dapat diperoleh bahwa turunan dari f(x) = cos x adalah f’(x) = –sin x.
Cara mendapatkan mendapatkan hasil turunan menggunakan definisi turunan untuk fungsi trigonemetri yang lebih kompleks tentu akan menjadi rumit. Sehingga diperlukan cara lain untuk mendapatkan hasil turunan fungsi trigonometri dengan berbagai bentuk bahkan untuk fungsi yang sangat kompleks.
Cara yang lebih baik untuk digunakan adalah menggunakan beberapa teorema turunan dan hasil turunan fungsi trigonometri bentuk dasar. Dengan cara ini dapat diperoleh hasil turunan fungsi dengan cara lebih baik.
Ada enam bentuk fungsi trigonometri dasar dan hasil turunannya yang perlu diingat. Keenam fungsi tersebut adalah fungsi sinus (sin x); cosinus (cos x); tangen (tan x); cotangan (cotan x); secan (sec x); dan cosecan (cosec x). Fungsi dan turunan keenam fungsi trigonometri bentuk dasar tersebut diberikan seperti tabel berikut.

Selain enam rumus dasar, beberapa hasil turunan fungsi trigonometri yang perlu juga diketahui diberikan pada daftar berikut.
- y = sin ax
y’ = a cos ax - y = p sin x
y’ = p cos x
- y = cos bx
y’ = b cos bx - y = q sin x
y’ = q cos x
- y = sin ax + cos bx
y’ = a cos ax ‒ b sin ax
Beberapa hasil turunan rumus fungsi trigonometri bentuk dasar di atas akan mempermudah mengerjakan soal turunan fungsi trigonometri yang lebih sulit.
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan sebagai tolak ukur pemahaman bahasan di atas. Contoh-contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahsan tersebut sebagai parameter keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Turunan Fungsi Trigonometri
Turunan pertama dari f(x) = 3 sin x ‒ 4 cos x + 2 adalah ….
A. 3 cos x + 4 sin x
B. 3 sin x + 4 cos x
C. ‒3 cos x + 4 cos x
D. 3 cos x ‒ 4 sin x
E. ‒3 cos x ‒ 4 cos x
Pembahasan:
Turunan pertama fungsi f(x) = 3 sin x ‒ 4 cos x + 2 ditunjukkan seperti cara berikut.
Turunan fungsi f(x):
f’(x) = d(3 sin x)/dx ‒ d(4 cos x)/dx + d(2)/dx
f’(x) = 3·d(sin x)/dx ‒ 4·d(cos x)/dx + 0
f’(x) = 3cos x ‒ 4(‒sin x)
f’(x) = 3cos x + 4sin x
Jadi, turunan pertama dari f(x) = 3 sin x ‒ 4 cos x + 2 adalah 3cos x + 4sin x.
Jawaban: A
Contoh 2 – Soal Turunan Fungsi
Turunan pertama dari y = 1/4 sin 4x adalah ….
A. –1/4 cos 4x
B. 1/4 cos 4x
C. –4 cos 4x
D. cos 4x
E. 4 cos 4x
Pembahasan:
Untuk menentukan turunan pertama dari fungsi tersebut dilakukan dengan aturan rantai dan informasi turunan pertama fungsi y = sin x adalah y’ = cos x.
Misalkan u = 4x → y = 1/4 sin u
Sehingga, dapat dipeorleh nilai dy/du dan du/dx seperti berikut.
- dy/du = 1/4 cos u
- du/dx = 4
Mencari turunan pertama fungsi y = 1/4 sin 4x:
dy/dx = dy/du · du/dx
dy/dx = 1/4 cos u · 4
dy/dx = 4 1/4 cos u = cos 4x
Jadi, turunan pertama dari y = 1/4 sin 4x adalah cos 4x.
Jawaban: D
Contoh 3 – Soal Turunan Fungsi

Pembahasan:
Bentuk soal yang diberikan di atas dapat diselesaikan dengan teknik yang sama dengan penyelesaian contoh 1. Di sini digunakan pemisalan u = 2x–5/3x–1 sehingga f(x) = cos2u. Cara mencari turunan pertama fungsi f(x) ditunjukkan seperti cara penyelesaian di bawah.

Jadi, turunan dari f(x) = cos2 (2x‒5/3x‒1) adalah ‒13/(3x‒1)2 sin 2(2x‒5/3x‒1).
Jawaban: B
Contoh 4 – Soal Turunan Fungsi
Turunan pertama dari fungsi f(x) = cos32x adalah ….
A. 6 · cos22x · sin 2x
B. ‒6 · cos22x · sin 2x
C. ‒6 · cos 2x · sin 2x
D. 3 · cos 2x · sin 4x
E. ‒3 · cos 2x · sin 2x
Pembahasan:
Turunan pertama f(x) = cos32x dapat diselesaikan dengan aturan rantai seperti penyelesaian berikut.
Misalkan:
u = 2x → du/dx = 2
v = cos u → dv/du = ‒sin u
Turunan f(x) = cos32x
f(x) = cos32x = v3
f’(x) = df(x)/dv × dv/du × du/dx
f’(x) = 3v2 × ‒sin u × 2
f’(x) = 3 × cos2u × ‒sin u × 2
f’(x) = ‒6 · cos22x · sin 2x
Jadi, turunan pertama dari fungsi f(x) = cos32x adalah ‒6 · cos22x · sin 2x.
Jawaban: B
Demikianlah tadi bahasan materi turunan fungsi trigonometri yang dilengkapi dengan contoh soal beserta pembahasan. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Aplikasi Turunan – Mencari Luas Maksimum/Minimum Suatu Daerah
