Ukuran penyebaran data terdiri dari jangkauan, hamparan, simpangan rata-rata, variansi, dan simpangan baku. Fungsinya untuk mengetahui seberapa jauh data-data menyebar dari pusat data. Ukuran penyebaran data menggambarkan kondisi pemencaran data kuantitatif.
Rumus ukuran penyebaran data lebih detailnya ada di bawah.
Daftar isi:
Rumus Ukuran Penyebaran Data
Ukuran penyebaran data terdiri dari jangkauan (range), simpangan rata-rata, jangkauan antar kuartil, Stdv. Ketiga rumus ukuran penyebaran data ada di bawah.
1) Jangkauan (J)
Jangkauan adalah selisih nilai terbesar dan terkecil.
Jangkauan merupakan ukuran penyebaran yang sangat kasar. Semakin kecil nilai jangkauan, semakin baik kualitas data. Sebaliknya, nilai jangkauan yang besar menunjukkan kualitas data yang tidak baik.
Rumus jangkauan:
J = xmax – xmin
- Keterangan:
- J = jangkauan
- xmax = nilai tertinggi
- xmin = nilai terendah
Cara menghitung jangkauan:
Soal:
Jangkauan dari data 3, 6, 10, 5, 8, 9, 6, 4, 7, 5, 6, 9, 5, 2, 4, 7, 8 adalah ….
Jawab:
Data yang sudah diurukan dari terkecil ke terbesar → 2, 3, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 8, 8, 9, 9, dan 10.
Diperoleh data terbesar adalah xmax = 10. Sedangkan data terkecil adalah xmin = 2.
Sehingga,
Jangkauan = 10 – 2
Jangkauan = 8
Jadi, jangkauan dari data 3, 6, 10, 5, 8, 9, 6, 4, 7, 5, 6, 9, 5, 2, 4, 7, 8 adalah 8.
2) Simpanga Rata-rata
Simpangan rata-rata disebut juga deviasi rata-rata. Nilai simpangan rata-rata sama dengan rata-rata jarak setiap titik nilai ke rata-rata data.
Misalkan, data hasil pengamatan x1, x2, …, dan xn memiliki rata-rata x̅. Jarak setiap titik data dengan rata-ratanya adalah |xi – x̅|. Simpangan rata-rata adalah rata-rata jarak setiap datum dengan rata-rata data.
Rumus simpangan rata-rata:
Cara menghitung simpangan rata-rata
Soal:
Simpangan rata-rata dari data 5, 6, 4, 6, 8, 8, 7, 4 adalah ….
Jawab:
Diketahui jumlah data = 5 + 6 + 4 + 6 + 8 + 8 + 7 + 4 = 48 dan banyak data n = 8.
Menghitung rata-rata:
Menghitung simpangan rata-rata:
Sebelumnya, hitung rata-rata selisih jaraknya.
| data ke-i | Seisih jarak |
| 5 | |5 – 6| = 1 |
| 6 | |6 – 6| = 0 |
| 4 | |4 – 6| = 2 |
| 6 | |6 – 6| = 0 |
| 8 | |8 – 6| = 2 |
| 8 | |8 – 6| = 2 |
| 7 | |7 – 6| = 1 |
| 4 | |4 – 6| = 2 |
Sehingga,
Jadi, simpangan rata-rata dari data 5, 6, 4, 6, 8, 8, 7, 4 adalah 5/4.
Baca Juga: Penyajian Data Kelompok (Histogram, Poligon, dan Ogive)
3) Variansi dan Simpangan baku
Variansi disebut juga dengan ragam. Rumus variansi adalah selisih kuadrat setiap data terhadap rata-rata hitungnya.
Simpangan baku disebut juga standar deviasi. Rumus simpangan baku adalah akar kuadrat positif dari varians. Nilai simpangan baku menunjukkan standar penyimpangan data terhadap nilai rata-ratanya.
Rumus ragam dan simpangan baku:
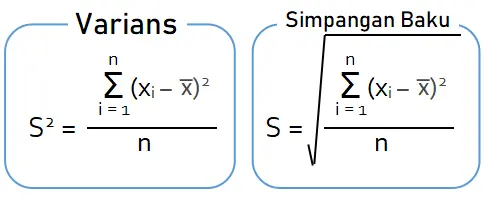
- Keterangan:
- n = banyak data
- S2 = varians (ragam)
- S = simpangan baku (standar deviasi)
- xi = data ke-i
- x̅ = rata-rata data
- Ʃ = notasi sigma (operasi jumlah)
Cara menghitung varians dan simpangan baku:
Soal:
Diketahui data 2, 6, 7, 1, 4. Varians dan simpangan baku data tersebut adalah ….
Jawab:
Diketahui jumlah data = 2 + 6 + 7 + 1 + 4 = 20 dan banyak data n = 5.
Rata-rata data
Menghitung selisih kuadrat terhadap rata-rata:
| data ke-i | selisih kuadrat |
| 2 | = (2 – 4)2 = 4 |
| 6 | = (6 – 4)2 = 4 |
| 7 | = (7 – 4)2 = 9 |
| 1 | = (1 – 4)2 = 9 |
| 4 | = (4 – 4)2 = 0 |
Jumlah selisih kuadrat setiap data terhadap rata-rata hitung: Ʃ(xi – x̅)2 = 4 + 4 + 9 + 9 + 0 = 26.
Sehingga,
Ukuran Penyebaran Data Lainnya
Selain jangkauan, simpangan rata-rata, varians, dan simpangan baku. Ukuran penyebaran data juga meliputi jangkauan interkuartil (hamparan) dan simpangan kuartil (Qd).
Rumus ukuran penyebaran data untuk jangkauan interkuartil dan simpangan kuartil ada di bawah.
4) Jangkauan Interkuartil (H)
Jangkauan antar kuartil atau jangkauan antar kuartil sama dengan hamparan (H). Nilai jangkauan interkuartil sama dengan selisih kuartil atas dengan kuartil bawah.
Kuartil adalah nilai yang membagi data menjadi empat sama banyak. Ada tiga nilai kuartil yaitu kuartil bawah (Q1), kuartil tengah (Q2), dan kuartil atas (Q3).
Rumus hamparan:
H = Q3 – Q1
- Keterangan:
- H = hamparan (jangkauan interkuartil)
- Q3 = kuartil atas
- Q1 = kuartil bawah
Cara menghitung hamparan:
Soal:
Hamparan dari sekelompok data 16, 7, 10, 14, 9, 14, 11, 12, 9, 12 adalah ….
Jawab:
Data yang telah diurutkan → 7, 9, 9, 10, 11, 12, 12, 14, 14, 16 (banyak data = 10)
Kuartil tengah membagi data menjadi dua sama banyak yaitu 7, 9, 9, 10, dan 11 dengan 12, 12, 14, 14, dan 16.
Kuartil bawah = nilai yang membagi sekolompok data 7, 9, 9, 10, dan 11 sama banyak. Nilai kuartil bawah adalah Q1 = data ke-5+1/2 = data ke-3 = 9. Kuartil atas = nilai yang membagi sekolompok data 12, 12, 14, 14, dan 16 sama banyak. Nilai kuartil atas adalah Q3 = data ke-5+1/2 = data ke-3 = 14.
Sehingga nilai hamparannya adalah H = Q3 – Q1 = 14 – 9 = 5.
5) Simpangan Kuartil (Qd)
Simpangan kuartil disebut juga jangkauan semi interkuartil. Nilai simpangan kuartil sama dengan setengah dari hamparan.
Rumus simpangan kuartil:

- Keterangan:
- Qd = simpangan kuartil
- Q3 = kuartil atas
- Q1 = kuartil bawah
Cara menghitung simpangan kuartil:
Soal:
Simpangan kuartil dari 7, 4, 5, 6, 7, 4, 5, 7, 8, 9, 6 adalah ….
Jawab:
Data yang sudah diurutkan → 4, 4, 5, 5, 6, 6, 7, 7, 7, 8, 9 (banyak data = 11)
Kuartil tengah membagi sekelompok data menjadi dua yaitu 4, 4, 5, 5, dan 6 dengan 7, 7, 7, 8, 9. Nilai tengah dari setengah data pertama merupakan kuartil bawah. Dan nilai tengah dari setengah data lainnya merupakan kuartil atas.
- Nilai
- Kuartil bawah = nilai tengah dari 4, 4, 5, 5, 6 → Q1 = 5
- Kuartil atas = nilai tengah dari 7, 7, 7, 8, 9 → Q3 = 7
Sehingga,
Jadi, simpangan kuartil dari 7, 4, 5, 6, 7, 4, 5, 7, 8, 9, 6 adalah 1.
Baca Juga: Rumus Kuartil, Desil, dan Persentil
Contoh Soal Ukuran Penyebaran Data
Soal ukuran penyebaran data dan pembahasannya ada di bawah.
Contoh 1
Perhatikan tabel di bawah!
| Berat Badan | Frekuensi |
| 50 – 54 | 4 |
| 55 – 59 | 6 |
| 60 – 64 | 8 |
| 65 – 69 | 10 |
| 70 – 74 | 8 |
| 75 – 79 | 4 |
Hamparan dari data yang diberikan pada tabel di atas adalah ….
A. 11,25
B. 22,50
C. 23,0
D. 59,5
E. 70,5
Pembahasan:
Dari soal dapat diketahui jumlah data = 4 + 6 + 8 + 10 + 8 + 4 = 40 dan banyak data n = 6.
Letak kuartil bawah dan atas:
- Kuartil bawah:
Q1 = data ke-(¼×40)
Q1 = data ke-10 - Kuartil atas:
Q3 = data ke-(¾×40)
Q3 = data ke-30
Menentukan letak kuartil bawah dan atas:
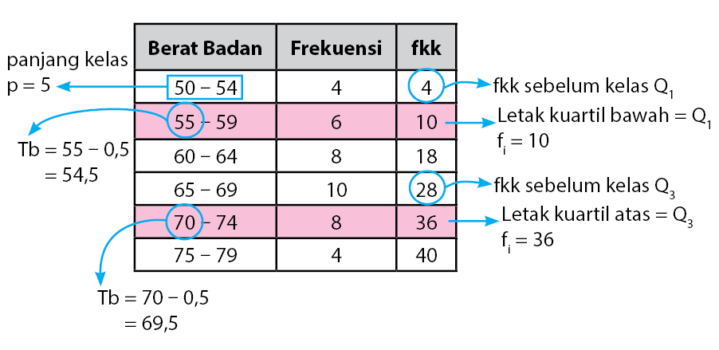
1) Menghitung kuartil bawah:
2) Menghitung kuartil atas:
Diperoleh nilai Q1 = 59,5 dan Q3 = 70,75
Sehingga,
Hamparan (H) = jangakaun atar kuartil
H = Q3 – Q1
H = 70,75 – 59,5 = 11,25
Jadi, hamparan dari data yang diberikan pada tabel di atas adalah 11,25.
Jawaban: A
Contoh 2
Diketahui data: 7, 4, 7, 5, 3, 9, 8, 7, 6, 4
(1) jangkauan = 6
(2) mean = 6
(3) modus = 7
(4) median = 6,5
Pernyataan yang benar dari data tersebut adalah ….
A. (1), (2), dan (3)
B. (1) dan (3)
C. (2) dan (4)
D. (4) saja
E. semua benar
Pembahasan:
Jangkauan merupakan ukuran penyebaran data. Sementara mean, modus, median merupakan ukuran pemusatan data.
Data yang sudah diurutkan:
3, 4, 4, 5, 6, 7, 7, 7, 8, 9
Jangkauan
= xmaks – xmin
= 9 – 3 = 6
Menghitung mean (rata-rata)
Menghitung median
Modus = data yang memiliki frekuensi paling banyak = 7
Diperoleh nilai jangkauan = 6; mean = 6; median = 6,5; dan modus = 7. Jadi, pernyataan yang benar dari data tersebut adalah nomor (1), (2), (3), dan (4) → semuanya benar.
Sekian pembahasan mengenai ukuran penyebaran data. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

maaf kak kalau saya hitung kembali dapat 11,25. Bagaimana ya?
Mohon maaf, angka 36 sebagai pembagi (1/4n – fkk) itu di dapat dari mana ya? Bukankah harusnya dibagi dengan nilai frekuensi pada kelas Q1 ya? Begitu juga untuk yang Q3
Iya kah kak?
Halo Bekti, terima kasih komentar dan koreksinya. Untuk kesalahan tersebut sudah diperbaiki yaa… Di mana untuk pembagi (1/4n – fkk) adalah frekuensi kelas letak Q1 dan pembagi (3/4n – fkk) adalah frekuensi kelas letak Q3. Salam sukses selalu!!