Contoh cara menghitung kuartil pada data tunggal, misalnya terdapat sepuluh data terurut 3, 4, 5, 6, 8, 8, 8, 9, 9, dan 10. Nilai kuartil tengah (Q2) berada di antara data ke-5 dan data ke-6, sehingga nilai kuartil tengah adalah Q2=(8+8) : 2 = 8. Nilai kuartil tengah membagi data menjadi dua sama banyak. Setengah bagian pertama dari data terutut tersebut adalah 3, 4, 5, 6, 8, dan 8 sementara setengah data terurut lainnya adalah 8, 8, 9, 9, dan 10.
Pada setengah bagian pertama memuat nilai kuarti bawah (Q1), sedangkan setengah bagian kedua memuat nilai kuarti atas (Q3).
Dari setengah bagian data pertama memuat nilai kuarti bawah (Q1). Di mana, nilai kuartil pada contoh data yang diberikan terdapat pada data ke-3 yaitu nilai yang membagi data menjadi dua sama banyak. Sehingga nilai kuartil bawah dari data tersebut adalah Q1= 5.
Selanjutnya, setengah bagian kedua dari dari data terurut yaitu 8, 8, 9, 9, dan 10 memuat nilai kuarti atas (Q3). Nilai yang membagi dua data tersebut sama banyak juga terdapat pada urutan data ke-3 dari setengah bagian data kedua atau data ke-8 dari semua data. Sehingga kuartil atas dari data adalah Q3= 9.
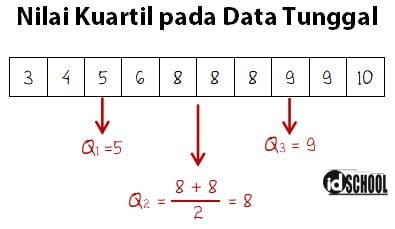
Dengan demikian diperoleh nilai untuk kuartil bawah, tengah, dan atas dari data terurut 3, 4, 5, 6, 8, 8, 8, 9, 9, dan 10 adalah Q1= 6, Q2 = 8, dan Q3 = 9.
Apa itu nilai kuartil? Bagaimana cara menghitung kuartil dari data kelompok? Bagaimana bentuk-bentuk contoh soal kuartil? Sobat idschool dapat mencari tahu jawabannya melalui ulasan cara menghitung kuartil atas, tengah, dan bawah melalui ulasan-ulasan berikut.
Table of Contents
- Apa Itu Nilai Kuartil?
- Rumus Kuartil Data Kelompok
- Soal 1 – Cara Menghitung Kuartil Atas
- Soal 2 – Cara Menghitung Kuartil dari Tabel Data Kelompok
- Soal 3 – Cara Menghitung Kuartil Tengah dari Histogram Data Kelompok
- Soal 4 – Mencari Frekuensi Kelas Kuartil dari Tabel Data Kelompok
- Soal 5 – Cara Menghitung Kuartil dan Frekuensi Kelas Kuartil
- Soal 6 – Variasi Bentuk Soal Cara Menghitung Kuartil
- Soal 7 – Variasi Bentuk Soal Cara Menghitung Kuartil
Apa Itu Nilai Kuartil?
Kuartil adalah nilai pembatas pada data terurut yang dibagi menjadi empat bagian sama banyak. Ada tiga nilai kuartil yang terdiri dari kuartil bawah (Q1), tengah (Q2), dan atas (Q3).
Nilai kuartil bawah, tengah, dan atas pada data tunggal dapat diperoleh dengan membagi data terurut menjadi dua sama banyak sehingga dapat diperoleh nilai kuartil tengah (Q1). Selanjutnya, setiap bagian dari dua bagian data terbagi tersebut dibagi lagi menjadi dua sama banyak.
Dari 1/2 bagian data terurut pertama akan diperoleh nilai kuartil bawah (Q1), sedangkan dari 1/2 bagian data terurut lainnya akan diperoleh kuartil atas (Q3). Seperti yang ditunjukkan pada contoh pada awal pembahasan pada bagian awal paragraf.
Pada data kelompok, nilai kuartil berada pada suatu interval kelas, sehingga membutuhkan suatu cara menghitung kuartil untuk data kelompok. Cara menghitung kuartil atas, tengah, dan bawah pada data kelompok dapat menggunakan rumus kuartil data kelompok.
Baca Juga: Cara Menghitung Median Data Kelompok (+Contoh Soal dan Pembahasannya)
Rumus Kuartil Data Kelompok
Pada penyajian data kelompok, nilai kuartil terletak pada suatu interval kelas. Di mana, nilainya dapat ditentukan dengan bantuan rumus kuartil data kelompok.
- Q1 (kuartil bawah): nilai yang menjadi batas dari data terurut yang paling rendah sampai 1/4 bagian data terurut pertama.
- Q2 (kuartil tengah): nilai yang membagi banyak data menjadi dua bagian yang sama banyak. Nilai kuartil tengah (Q2) disebut juga sebagai median yaitu nilai yang terletak antara dua bagian dari data terurut.
- Q3(kuatil atas): adalah nilai pembatas antara 3/4 data terurut pertama dengan 1/4 data terakhir.
Rumus kuartil bawah, tengah, dan atas yang dapat digunakan paca cara menghitung kuartil data kelompok sesuai dengan persamaan berikut.

Baca Juga: Rumus Mean Median Modus pada Data Tunggal
Selanjutnya sobat idschool dapat mempelajari bagaimana penggunaan rumus dan cara menghitung kuartil data kelompok dengan berbagai bentuk soal. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana cara menghitung kuartil.
Sobat idschool dapat menggunakan pembahasan cara menghitung kuartil tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Soal 1 – Cara Menghitung Kuartil Atas
Tabel berikut menyajikan data berat badan sekelompok siswa.

Kuartil atas data dalam tabel tersebut adalah ….
A. 664/6
B. 665/6
C. 671/6
D. 675/6
E. 681/6
Pembahasan:
Pertama, sobat idschool perlu mengetahui banyak data dari penyajian data yang diberikan yaitu dengan menjumlahkan seluruh frekuensinya.
Banyak data (n):
n = 3 + 6 + 10 + 12 + 15 + 6 + 4
n = 56
Dari banyak data tersebut dapat diketahui letak nilai kuartil atas (Q3). Nilai Q3 terletak antara data ke-3/4×56 [data ke-42] dan data ke-(3/4×56 + 1) [data ke-43] yaitu interval kelas 65–69.
Nilai batas bawah kelas Q3 adalah Tb = 64,5 dengan frekuensi kelas kuartil atas adalah f Q3 = 12. Dengan frekuensi komulatif kurang dari kelas kuartil atas adalah fkk = 3 + 6 + 10 + 12 = 31. Panjang kelas pada penyajian tabel data kelompok adalah ℓ = 49,5 – 44,5 = 54,5 – 49,5 = … = 5.
Cara menghitung kuartil atas dapat dilakukan seperti pada langkah berikut.

Jadi, kuartil atas data dalam tabel tersebut adalah 681/6.
Jawaban: E
Soal 2 – Cara Menghitung Kuartil dari Tabel Data Kelompok

Pembahasan:
Pertama, hitung banyak data dari penyajian data yang diberikan dengan cara menjumlahkan semua nilai f (frekuensi).
Banyak data (n):
n = 4 + 10 + 18 + 24 + 16 + 8
n = 80
Letak nilai kuartil ketiga (Q3) terdapat di antara data ke–(3/4 × 80) data ke–(3/4 × 80 + 1) yaitu antara data ke-60 dan data ke-61 (interval kelas 63 – 67).
Sehingga dapat diketahui bahwa batas bawah kelas Q3 (Tb) = 62,5; frekuensi kelas Q3 (fQ3) = 16; dan frekuensi komulatif kurang dari kelas Q3 (fkk) = 56. Di mana panjag kelas pada penyajian data kelompok tersebut adalah ℓ = 47,5 – 42,5 = 52,5 – 47,5 = … = 5.

Cara menghitung kuartil atas atau nilai kuartil ketiga (Q3):

Jadi, kuartil ketiga dari data yang disajikan dalam histogram berikut adalah 63,75
Jawaban: B
Baca Juga: Ukuran Penyebaran Data – Jangkauan, Hamparan, dan Kuartil
Soal 3 – Cara Menghitung Kuartil Tengah dari Histogram Data Kelompok
Perhatikan data kelompok pada histogram berikut!
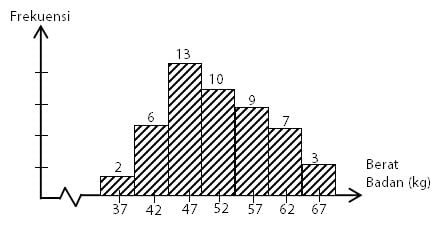
Kuartil ke-2 dari data berat badan yang ditunjukkan pada histogram di atas adalah ….
A. 50,5 kg
B. 51,5 kg
C. 52,5 kg
D. 53,5 kg
E. 54,5 kg
Pembahasan:
Pertama, sobat idschool perlu mengetahui banyak data pada penyajian histogram dengan cara menjumlahkan semua nilai frekuensinya.
Banyak data:
n = 2 + 6 + 13 + 10 + 9 + 7 + 3
n = 50
Letak kuartil ke-2 (Q2) atau kuartil tengah berada di antara data ke-(2/4 × 50) data ke-(2/4 × 50 + 1) yaitu anatar data ke-25 dan data ke-26 (kelas dengan titik tengah 52).
Sehingga dapat diperoleh batas bawah kelas dengan kuartil tengah adalah Tb = (52 + 47) : 2 = 49,5. Frekuensi kelas kuartil tengah adalah fQ2 = 9 dan frekuensi komulatif kurang dari kelas kuartil tengah adalah fkk = 21. Panjang kelas pada penyajian data kelompok bentuk histogram tersebut adalah ℓ = 39,5 – 34,5 = 44,5 – 39,5 = …. = 5.
Cara menghitung kuartil tengah:

Jadi, kuartil ke-2 (Q2) dari data berat badan yang ditunjukkan pada histogram di atas adalah 51,5 kg
Jawaban: B
Soal 4 – Mencari Frekuensi Kelas Kuartil dari Tabel Data Kelompok

Baca Juga: Cara Menghitung Desil dan Persentil Data Kelompok
Pembahasan:
Diketahui nilai kuartil atas adalah 49,25 sehingga letak nilai kuartil atas berada di interval kelas 44 – 49. Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi berikut.
- Banyak data: n = 4 + 6 + 6 + 10 + k + 8 + 4 = 38 + k
- Nilai kuartil atas: Q3 = 49,25
- Batas bawah kelas kuatil Q3: Tb = 43,5
- Frekuensi komulatif kurang dari kelas Q3: fkk = 26
- Frekuensi kelas kuartil atas: fQ3 = k
- Panjang kelas: ℓ = 25,5 – 19,5 = 31,5 – 25,5 = … = 6
Mencari nilai k:
Q3 = Tb + ℓ × (3/4×n – fkk) : fQ3
49,25 = 43,5 + 6×(3/4×(38 + k) – 26) : k
49,25 – 43,5 = 6×(3/4×(38 + k) – 26) : k
5,75k = 9/2×38 + 9/2k – 6×26
5,75k – 9/2k =171 – 156
5,75k – 9/2k = 15
1,25k = 15
k = 15 : 1,25 = 12
Sehingga diperoleh nilai k = 12
Jawaban: D
Soal 5 – Cara Menghitung Kuartil dan Frekuensi Kelas Kuartil
Perhatikan penyajian data kelompok dalam bentuk histogram berikut!

Jika kuartil bawah dari data nilai ulangan harian di atas adalah 73,5 maka nilai q = ….
A. 10
B. 11
C. 12
D. 13
E. 14
Pembahasan:
Diketahui nilai kuartil bawah adalah Q1 = 73,5 sehingga nilai kuartil terletak pada kelas dengan titik tengah 75. Dengan demikian dapat diperoleh nilai-nilai seperti berikut:
- Banyak data: n = 3 + 5 + q + 9 + 8 + 5 = 30 + q
- Batas bawah kelas letak Q1: Tb = (75 + 70) : 2 = 72,5
- Frekuensi kelas kuartil bawah: fQ1 = q
- Frekuensi komulatif kurang dari kelas kuartil bawah (Q1): fkk = 8
Cara menghitung frekuensi kuartil bawah (Q1):

Jawaban: A
Baca Juga: Penyajian Data dalam Bentuk Ogive
Soal 6 – Variasi Bentuk Soal Cara Menghitung Kuartil
Diketahui 10 bilangan genap berurutan yang nilainya berbeda. Jika kuartil pertama bilangan-bilangan tersebut adalah 32 maka mediannya adalah ….
A. 34
B. 35
C. 36
D. 37
E. 38
Pembahasan:
Misalkan nilai 10 bilangan genap berurutan tersebut adalah x1, x2, . . ., dan x10. Letak median atau kuartil kedua (Q2) berada di antara bilangan e dan f. Sedangkan kuartil bawah dari data sepuluh bilangan tersebut adalah nilai x3 = 32.

Diketahui bahwa sepuluh bilangan tersebut merupakan bilangan genap berurutan yang nilainya berbeda. Sehingga, nilai x5 dan x6 berturut-turut adalah 36 dan 38. Jadi, nilai mediannya adalah Q2 = (36 + 38 ) : 2 = 37.
Jawaban: D
Soal 7 – Variasi Bentuk Soal Cara Menghitung Kuartil
Sepuluh siswa mengikuti suatu tes. Jika nilai tes tersebut memiliki jangkauan 45 dengan nilai terendah 50 dan kuartil ketiga 90 maka tiga nilai tertinggi siswa tersebut yang paling mungkin adalah ….
A. 90; 95; dan 100
B. 85; 90; dan 95
C. 90; 90; dan 100
D. 90; 90; dan 95
E. 85; 95; dan 95
Pembahasan:
Misalkan data terurut untuk nilai kesepuluh siswa yang mengikuti tes adalah x1, x2, …, dan x10. Sehingga, berdasarkan keterangan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Jangkauan: x10 – x1 = 45
- Nilai terendah: x1 = 50
- Kuartil ketiga: Q3 = 90
Mencari nilai tertinggi (x10) dari persamaan x10 – x1 = 45:
x10 – 50 = 45
x10 = 45 + 50 = 95
Diketahui bahwa kuartil ketiga (Q3) atau kuarti atas dari data terurut x1, x2, …, dan x10 adalah Q3 = x8 = 90.
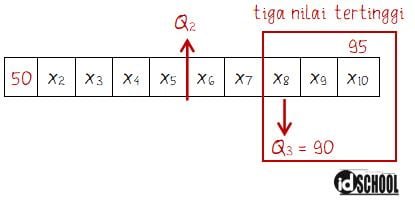
Jadi, tiga nilai tertinggi siswa tersebut yang paling mungkin adalah 90; 90; dan 95.
Jawaban: D
Demikanlah tadi ulasan cara menghitung kuartil atas, tengah, dan bawah. Terima kasih sudah mengunjungi halaman cara menghitung kuartil dari idschool(dot)net, semoga bermanfaat!
Baca Juga: Bentuk-Bentuk Soal pada TPS UTBK SBMPTN
