Cara Menghitung Besar Salah Satu Sudut Segitiga yang Belum Diketahui

Besar salah satu sudut segitiga yang belum diketahui dapat dihitung melalui selisih 180^o dengan jumlah besar dua sudut segitiga yang diketahui. Di mana besar nilai 180^o merupakan jumlah ketiga besar sudut segitiga yang dapat dibuktikan. Dengan diketahui dua besar sudut pada suatu segitiga maka besar salah satu sudut segitiga yang lainnya dapat dicari tahu melalui sebuah perhitungan.

Segitiga adalah sebuah bangun datar yang memiliki tiga sisi dan tiga titik sudut. Ada berbagai macam jenis segitiga yang dilihat dari panjang sisi -sisi segitiga dan besar sudut-sudut segitiga.

Jenis-jenis segitiga berdasarkan panjang sisi-sisinya terdiri dari segitiga sama sisi, sama kaki, siku siku, dan sembarang. Sementara jenis-jenis segitiga berdasarkan besar sudutnya terdiri dari segitiga tumpul dan segitiga lancip. Masing-masing jenis segitiga memiliki sifat atau karakteristiknya sendiri.

Hubungan besar sudut-sudut dalam segitiga memiliki karakteristik yang dapat dinyatakan dalam suatu persamaan. Karakteristik pada segitiga memungkinkan untuk mengetahui besar sudut-sudut dalam segitiga. Bagaimanakah cara menghitung besar salah satu sudut segitiga yang belum diketahui? Sobat idschool dapata mencari tahu jawabannya melalui ulasan di bawah,

Table of Contents

• Bukti Jumlah Ketiga Sudut pada Segitiga = 180o
• Langkah-Langkah untuk Menghitung Besar Salah Satu Sudut Segitiga yang Belum Diketahui
• Contoh Soal dan Pembahasan
  • Contoh 1 – Soal Mencari Besar Salah Satu Sudut Segitiga yang Belum Diketahui
  • Contoh 2 – Soal Besar Salah Satu Sudut Segitiga
  • Contoh 3 – Soal Besar Salah Satu Sudut Segitiga

Bukti Jumlah Ketiga Sudut pada Segitiga = 180^o

Besar jumlah ketiga jumlah sudut pada segitiga sama dengan besar sudut pada garis lurus. Dari mana kesimpulan tersebut diperoleh? Sobat idschool dapat membuktikannya melalui sebuah percobaan sederhana berikut.

Buat segitiga sembarang dengan penanda pada masing-masing sudutnya. Potong ketiga sudut pada segitiga kemudian gabungkan ketiga sudutnya. Sobat idschool akan mendapatkan bahwa susunan ketiga sudut tersebut membentuk sebuah garis lurus.

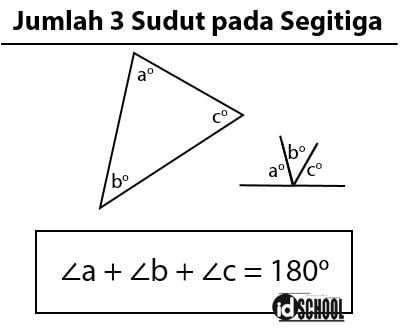
Diketahui bahwa besar sudut pada sebuah garis lurus sama dengan 180^o. Dapat ditunjukkan bahwa jumlah besar ketiga sudut pada segitiga sama dengan besar sudut garis lurus. Sehingga dapat diperoleh kesimpulan bahwa jumlah besar ketiga sudut pada segitiga sama dengan 180^o (180 derajat).

Misalkan, terdapat sebuah segitiga sembarang memiliki tiga sudut yaitu ∠a, ∠b, dan ∠c. Maka jumlah ∠a + ∠b + ∠c = 180^o. Persamaan untuk jumlah ketiga sudut pada segitiga tersebut berlaku pada semua jenis segitiga.

Baca Juga: Segitiga Siku-Siku dengan Sudut Istimewa

Langkah-Langkah untuk Menghitung Besar Salah Satu Sudut Segitiga yang Belum Diketahui

Untuk mendapatkan besar salah satu sudut segitiga maka besar dua sudut segitiga yang lainnya perlu diketahui. Caranya menggunakan perhitungan selisih antara jumlah kedua besar sudut segitiga yang diketahui dengan 180^o. Ringkasnya, cara menentukan besar salah satu sudut segitiga yang belum diketahui dapat mengikuti langkah-langkah berikut.

1. Menentukan besar dua sudut pada sebuah segitiga berdasarkan informasi yang diberikan.
2. Besar sudut yang belum diketahui = 180^o – (jumlah kedua besar sudut segitiga yang diketahui)

Misalkan pada sebuah segitiga terdapat ∠A, ∠B, dan ∠C dengan diketahui dua besar sudut ∠A dan ∠B. Besar ∠C pada segitiga tersebut dapat diketahui melalui persamaan besar ∠C = 180^o – (∠A + ∠B).

Baca Juga: Segi Empat Tali Busur dan Besar Sudut Antara Dua Tali Busur

Contoh Soal dan Pembahasan

Beberapa soal yang diberikan di bawah akan membantu sobat idschool lebih memadahi bagaimana cara menghitung besar salah satu sudut segitiga yang belum diketahui. Setiap contoh soal yang diberikan beserta dengan pembahasan soal. Pembahasan soal tersebut dapat sobat idschool gunakan sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih.

Contoh 1 – Soal Mencari Besar Salah Satu Sudut Segitiga yang Belum Diketahui

Perhatikan gambar di bawah!

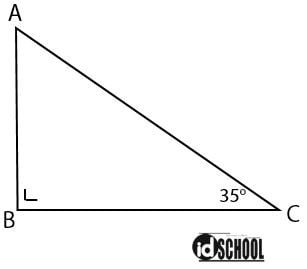
Besar sudut A adalah ….
A. 35^o
B. 45^o
C. 55^o
D. 90^o

Pembahasan:
Berdasarkan keterangan pada soal dapat diperoleh informasi:

• Besar ∠ACB = 35^o
• Besar ∠ABC = 90^o (ada tanda tegak lurus)

Sehingga, besar sudut A atau besar ∠CAB adalah:
∠CAB = 180^o – (∠ACB + ∠ABC)
∠CAB = 180^o – (35^o + 90^o)
∠CAB = 180^o – 125^o = 55^o

Jadi, besar sudut A adalah 55^o.

Jawaban: C

Contoh 2 – Soal Besar Salah Satu Sudut Segitiga

Perhatikan gambar di bawah!

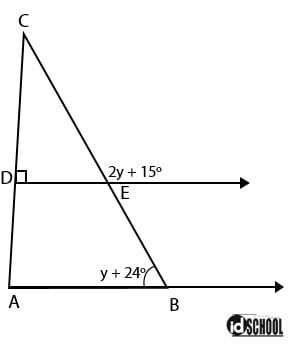
Berdasarkan gambar di atas, besar sudut ACB adalah ….
A. 19^o
B. 26^o
C. 40^o
D. 47^o

Pembahasan:
Besar ∠DEC sama dengan besar ∠ABC karena kedua sudut tersebut merupakan sudut sehadap. Selanjutnya terlihat bahwa gabungan sudut dengan besar y + 24^o dan 2y + 15^o membentuk garis lurus (besar sudutnya sama dengan 180^o).

Mencari nilai y:
2y + 15^o + y + 24^o = 180^o
2y + y = 180^o – 15^o – 24^o
3y = 141^o
y = 141^o : 3 = 47^o

Menghitung besar sudut ∠ABC = ∠DEC:
∠ABC = ∠DEC
∠ABC = y + 24^o
∠ABC = 47^o + 24^o = 71^o
∠ABC = ∠DEC = 71^o

Sebelum menentukan panjang salah satu sudut segitiga yang belum diketahui pada segitiga ACB, perhatikan segitiga DCE yang memiliki dua besar sudut seperti berikut.

• Besar ∠EDC = 90^o (ada tanda siku-siku)
• Besar sudut ∠DEC = ∠ABC = 71^o (hasil perhitungan sebelumnya)

Menghitung besar ∠ECD:
∠EDC + ∠DEC + ∠ECD = 180^o
90^o + 71^o + ∠ECD = 180^o
161^o + ∠ECD = 180^o
∠ECD = 180^o – 161^o = 19^o

Besar ∠ACB = besar∠DCE = 19^o.

Jawaban: A

Contoh 3 – Soal Besar Salah Satu Sudut Segitiga

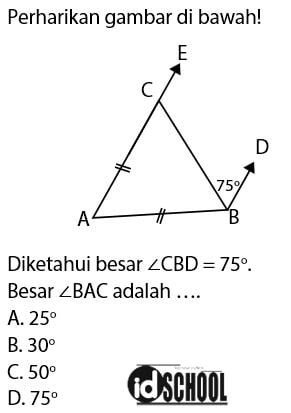
Pembahasan:
Segitiga ABC merupakan segitiga sama kaki, di mana sisi AC = AB. Pada segitiga sama kaki, besar dua sudut yang menghadap sisi segitiga yang sama juga akan sama besar. Sehingga, besar ∠ACB sama dengan besar ∠ABC.

Besar sudut ∠ACB = ∠DBC = 75^o karena keduanya merupakan pasangan sudut dalam berseberangan. Sehingga, besar ∠ABC = ∠ACB = 75^o karena keduanya merupakan sudut yang menghadap sisi segitiga sama kaki yang panjangnya sama.

Mencari besar ∠BAC:
∠ABC = 180^o – (75^o + 75^o)
∠ABC = 180^o – 150^o
∠ABC = 30^o

Jadi, besar ∠BAC sama dengan 30^o.

Jawaban: B

Demikianlah ulasan materi cara menghitung besar salah satu sudut segitiga yang belum diketahui. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Garis dan Sudut + Contoh Soal Beserta Pembahasannya