Ada beberapa cara menyelesaikan persamaan kuadrat yang antara lain dapat menggunakan rumus abc, melengkapkan kuadrat sepmpurna, dan pemfaktoran aljabar. Sebuah persamaan yang memiliki variabel dengan pangkat tertinggi sama dengan dua disebut sebagai persamaan kuadrat. Cara menyelesaikan persamaan kuadrat untuk mendapatkan solusi dari persamaan tersebut dapat dilakukan dengan berbagai cara atau trik. Setidaknya ada 4 (empat) cara yang dapat dilakukan untuk menyelesaikan persamaan kuadrat. Keempat cara menyelesaikan persamaan kuadrat tersebut adalah menggunakan rumus abc, pemfaktoran, melengkapkan kuadrat sempurna, dan menggunakan trik kucing.
Melalui halaman ini akan ditunjukkan pengerjaan satu soal yang sama dengan empat cara. Tujuannya adalah untuk menunjukkan bahwa keempat cara untuk menyelesaikan persamaan kuadrat akan menghasilkan hasil akhir yang sama. Akan ada dua persamaan kuadrat yang dijadikan contoh. Pertama adalah persamaan kuadrat dengan nilai koefisien pangkat tertinggi sama dengan satu. Kedua adalah koefisien pangkat tertinggi tidak sama dengan satu. Persamaan kuadrat yang akan diselesaikan dengan keempat cara tersebut adalah seperti berikut ini.

Melalui halaman ini, idschool akan mengulas keempat cara menyelesaikan persamaan kuadrat. Walaupun dikerjakan dengan cara yang berbeda, namun jika dikerjakan dengan benar maka akan menghasilkan hasil akhir yang sama. Sehingga nantinya, sobat idschool dapat memilih salah satu cara dari keempat cara yang menurut sobat idschool paling mudah.
Table of Contents
- 1) Cara Menyelesaikan Persamaan Kuadrat dengan Rumus abc
- 2) Cara Menyelesaikan Persamaan Kuadrat dengan Pemfaktoran
- 3) Penyelesaian Persamaan Kuadrat dengan Melengkapkan Kuadrat Sempurna
- 4) Menyelesaikan Persamaan Kuadrat dengan TRIK KUCING
1) Cara Menyelesaikan Persamaan Kuadrat dengan Rumus abc
Ulasan pertama yang akan diberikan adalah menyelesaikan persamaan kuadrat dengan rumus abc. Ingat kembali rumus abc yang dapat digunakan untuk menyelesaikan persamaan kuadrat.

Untuk menyelesaikan persamaan kuadrat menggunakan rumus abc, sobat idschool hanya perlu memasukkan koefisien dari persamaan kuadrat ke dalam rumus abc.
Menyelesaikan persamaan kuadrat x2 – 5x + 6 = 0 dengan rumus abc:
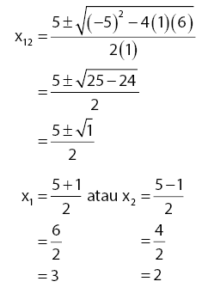
Dari hasil proses pengerjaan, diperoleh hasil akhir nilai x yang memenuhi persamaan kuadrat adalah 3 dan 2.
Selanjutnya, rumus abc akan digunakan untuk menyelesaikan persamaan kuadrat dengan nilai koefisien tertinggi tidak sama dengan 1.
Menyelesaikan persamaan kuadrat 2x2 – x – 3 = 0 dengan rumus abc:

Hasil akhir dari penyelesaian persamaan kuadrat 2x2 – x – 3 = 0 adalah x1 = 2/3 dan x2= ‒1.
Baca Juga: Lebih Lanjut Tentang Rumus abc
2) Cara Menyelesaikan Persamaan Kuadrat dengan Pemfaktoran
Berikutnya adalah cara menyelesaikan persamaan kuadrat dengan pemfaktoran. Untuk sobat idschool yang baru mempelajari cara ini, cara ini dapat dikatakan lebih susah dari cara pertama yang diberikan sebelumnya. Namun, cara ini dapat menyingkat waktu pengerjaan dan lebih efisien.
Untuk mereka yang sudah mahir dalam memahami langkah – langkah pengerjaan dengan cara ini. Tantangan terbesar dari cara menyelesaikan persamaan kuadrat dengan pemfaktoran adalah menebak bilangan yang sesuai.
Langkah-langkah menyelesaikan persamaan kuadrat dengan pemfaktoran:
Langkah 1:
mencari dua bilangan yang sesuai, kriterianya diberikan seperti pada gambar.
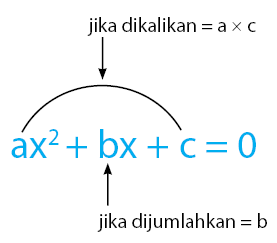
Langkah 2: menyusun persamaan
Langkah 3: melakukan manipulasi operasi aljabar sehingga diperoleh hasil akhir.
Sekarang, mari lihat proses pengerjaan persamaan kuadrat dengan cara pengerjaan untuk soal yang sama seperti yang diberikan di atas.
Contoh 1: Cara menyelesaikan persamaan kuadrat x2 – 5x + 6 = 0 dengan pemfaktoran
Langkah 1: Mencari dua bilangan jika dikalikan sama dengan 6 dan jika dijumlahkan sama dengan –5.

Bilangan tersebut adalah – 3 dan – 2.
Langkah 2: menyusun persamaan
x2 ‒ 5x + 6 = 0
(x ‒ 3)(x ‒ 2) = 0
Langkah 3: melakukan operasi aljabar sehingga diperoleh hasil akhir yang sesuai
x – 3 = 0 → x = 3
x – 2 = 0 → x = 2
Diperoleh dua nilai x yaitu 3 atau 2. Hasil ini sama dengan cara menyelesaikan persamaan kuadrat sebelumnya.
Contoh 2: Cara menyelesaikan persamaan kuadrat 2x2 – x – 3 = 0 dengan pemfaktoran
Langkah 1: Mencari dua bilangan jika dikalikan = –6 dan jika dijumlahkan = –1.
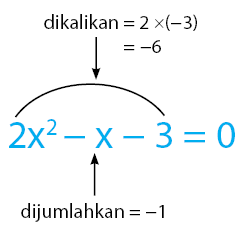
Kedua bilangan tersebut adalah – 3 dan 2.
Langkah 2: menyusun persamaan

Langkah 3: melakukan operasi aljabar sehingga diperoleh hasil akhir yang sesuai seperti langkah berikut.
x ‒ 3 = 0 → x = 3/2
x + 1 = 0 → x = ‒1
Diperoleh dua nilai x yaitu x1 = 3/2 dan x2 = ‒1
Baca Juga: Menggambar Grafik Persamaan Kuadrat
3) Penyelesaian Persamaan Kuadrat dengan Melengkapkan Kuadrat Sempurna
Kunci dari cara menyelesaikan persamaan kuadrat dengan melengkapkan kuadrat sempurna adalah melakukan manipulasi aljabar sehingga persamaan kuadrat mempunyai bentuk kuadrat sempurna. Sobat idschool pasti tahu angka yang memiliki akar kuadrat sempurna, seperti 1, 4, 9, 16, dan lain sebagainya. Angka-angka tersebut akan membantu proses pengerjaan menyelesaikan persamaan kuadrat dengan melengkapkan kuadrat sempurna.
Selain itu, bentuk-bentuk persamaan kuadrat sempurna juga diperlukan untuk menyelesaikan persamaan kuadrat dengan melengkapkan kuadrat sempurna.
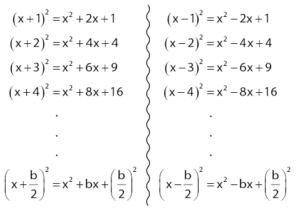
Contoh 1: Cara menyelesaikan persamaan kuadrat x2 – 5x + 6 = 0 dengan melengkapkan kuadrat sempurna
Melengkapkan bentuk kuadrat sempurna:
x2 ‒ 5x + 6 = 0
x2 ‒ 5x = ‒6
x2 ‒ 5x + (5/2)2 = ‒6 +(5/2)2
(x ‒ 5/2)2 = ‒6 + 25/4
(x ‒ 5/2)2 = ‒24/4 + 25/4
(x ‒ 5/2)2 = 1/4
x ‒ 5/2 = ± 1/2
Hasil akar pertama:
x1 ‒ 5/2 = 1/2
x1 = 1/2 + 5/2
x1 = 6/2 = 3
Hasil akar kedua:
x2 ‒ 5/2 = ‒1/2
x2 = ‒1/2 + 5/2
x2 = 4/2 = 2
Diperoleh nilai akar-akar dari persamaan kuadrat x2 ‒ 5x + 6 = 0 adalah 3 dan 2.
Contoh 2: Cara menyelesaikan persamaan kuadrat 2x2 – x – 3 = 0 dengan melengkapkan kuadrat sempurna
Melengkapkan bentuk kuadrat sempurna:
2x2 ‒ x ‒ 3 = 0
x2 ‒ 1/2x ‒ 3/2 = 0
x2 ‒ 1/2x = 3/2
x2 ‒ 1/2x + (1/4)2 = 3/2 + (1/4)2
(x ‒ 1/4)2 = 3/2 + 1/16
(x ‒ 1/4)2 = 24/16 + 1/16
(x ‒ 1/4)2 = 25/16
x ‒ 1/4 = ±5/4
Hasil akar pertama:
x1 ‒ 1/4 = 5/4
x1 = 5/4 + 1/4
x1 = 6/4 = 3/2
Hasil akar kedua:
x2 ‒ 1/4 = ‒5/4
x2 = ‒5/4 + 1/4
x2 = ‒4/4 = ‒1
Hasil akhir perhitungan menghasilkan nilai yang sama dengan dua cara menyelesaikan persamaan kuadrat sebelumnya, bukan?
Baca Juga: Pertidaksamaan Kuadrat dan Himpunan Penyelesaiannya
4) Menyelesaikan Persamaan Kuadrat dengan TRIK KUCING
Cara terakhir yang akan diulas untuk menyelesaikan persamaan kuadrat adalah trik kucing. Disebut demikian karena untuk menyelesaikan persamaan kuadrat dengan trik kucing menghasilkan gambar yang mirip dengan kucing. Menarik bukan? Simak cara yang akan diberikan cara berikut ini.
Langkah – langkah menyelesaikan persamaan kuadrat dengan trik kucing:
- Faktorkan pangkat tertinggi bersama dengan koefisienya
- Faktorkan nilai konstantanya
- Kalikan hasil pemfaktoran dengan aturan pada TRIK KUCING
- Jumlahkan hasil kali pemfaktoran
- Jika hasilnya tidak sama dengan nilai seperti pada bx maka tebakan yang dilakukan salah, ulangi sampai menemukan hasil yang benar.
- Susun hasil menyelesaikan persamaan kuadrat dengan cara TRIK KUCING
Menyelesaikan persamaan kuadrat x2 – x + 6 = 0 dengan TRIK KUCING:

Dari hasil pengerjaan juga diperoleh dua nilai, yaitu 3 atau 2.
- x – 3 = 0 → x = 3
- x – 2 = 0 → x = 2
Menyelesaikan persamaan kuadrat 2x2 – x – 3 = 0 dengan TRIK KUCING
Dari hasil pengerjaan juga diperoleh dua nilai, yaitu 2x ‒ 3 = 0 → x1 = 3/2 atau x + 1 = 0 → x2 = ‒1.
Sekian ulasan tentang cara menyelesaikan persamaan kuadrat melalui berbagai cara. Menurut idschool, cara yang paling mudah? Kalau mimin, untuk mengerjakan persamaan kuadrat dengan nilai a tidak sama dengan satu adalah dengan trik kucing. Sedangkan cara yang paling mudah untuk menyelesaikan persamaan kuadrat untuk nilai a sama dengan satu adalah cara pemfaktoran.
Bagaimana kalau menurut sobat idschool, cara mana yang paling mudah? Bisa beri tanggapan sobat idschool melalui komentar di bawah. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
