Karakteristik Segitiga dan Segi Empat

Segitiga dan segi empat merupakan bangun datar yang memiliki banyak sisi 3 (segitiga) dan 4 (segi empat). Karakteristik segitiga dan segi empat dapat dikenali melalui sifat dan bentuknya. Keduanya merupakan bangun yang sudah sobat idschool kenal sejak duduk di sekolah dasar. Segitiga mempunya tiga sisi dan tiga sudut. Sedangkan segi empat memiliki empat sisi dan sudut.

Di tingkat SMP, materi segitiga dan segi empat lebih diperdalam untuk meningkatkan kemampuan sobat idschool. Ulasan materi yang akan dibahas di sini adalah karakteristik segitiga dan segi empat.

Table of Contents

• Segitiga
• Segi Empat
  • Persegi
  • Persegi Panjang
  • Belah Ketupat
  • Jajar genjang
  • Layang-Layang
  • Trapesium
• Contoh Soal dan Pembahasan

Segitiga

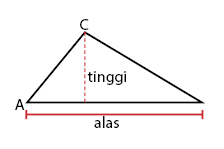
Ada beberapa bentuk segitiga antara lain meliputi segitiga siku-siku, sama kaki, dan sama sisi. Ketiga contoh segotiga yang disebutkan merupakan segitiga beraturan. Segitiga dapat dibedakan menjadi 2 berdasarkan sisi-sisi segitiga yaituuu segitiga beraturan dan tidak beraturan. Pembeda dari keduanya adalah keterangan panjang alas dan tinggi segitiga.

Pada segitiga beraturan, panjang sisi alas dan tinggi segitiga dapat diketahui. Sedangkan pada segitiga tidak beraturan tidak diketahui mana sisi yang merupakan alas segitiga dan masa tinggi segitiga tidak diketahui.

Rumus pada segitiga meliputi keliling dan alas yang sesuai dengan persamaan di bawah.

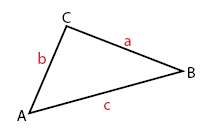
Keliling Segitiga: K_ΔABC = a + b + c

Luas Segitiga Beraturan ABC

Luas segitiga ABC tidak beraturan:

dengan s = ¹/₂×K_ΔABC = ¹/₂×(a + b + c)

Pada segitiga terdapat empat garis istimewa yang meliputi garis tinggi, bagi, berat, dan garis sumbu.

1. Garis Tinggi: Garis tinggi adalah garis yang ditarik dari salah satu titik sudut segitiga menuju sisi depan sudut dan tegak lurus terhadap sisi tersebut.

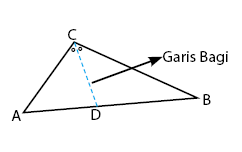
2. Garis Bagi: diperoleh dari garis yang ditarik dari salah satu titik sudut segitiga dan akan membagi sudut tersebut menjadi dua bagian sama besar.

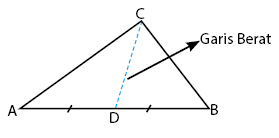
3. Garis Berat: garis yang ditarik dari salah satu titik sudut segitiga menuju sisi di depannya sehingga sisi terbagi menjadi dua sama panjang.

4. Garis Sumbu: Garis sumbu adalah garis yang ditarik dari pertengahansalah satu sisi segitiga dan tegak lurus dengan terhadap sisi tersebut.

 
Baca juga: Langkah-langkah melukis garis tinggi, garis bagi, garis berat, dan garis sumbu

Segi Empat

Pembahasan lanjutan mengenai karakteristik segitiga dan segi empat adalah bangun segi empat. Segi Empat yang akan dibahas pada bagian pembahasan kali ini meliputi persegi, persegipanjang, belah ketupat, jajar genjang, layang-layang, dan trapesium. 

Persegi

Karakteristik Persegi:

1. Mempunyai empat sisi yang sama panjang.
2. Memiliki empat buah titik sudut dengan besar masing-masing sudut adalah 90^o
3. Terdapat dua pasang sisi yang posisinya sejajar dan sama panjang.
4. Banyaknya simetri lipat adalah empat buah.
5. Simetri putar pada tingkat empat
6. Rumus keliling persegi: K = 4×s
7. Rumus luas persegi: Luas = s²

Persegi Panjang

Karakteristik persegi panjang:

1. Terdapat dua pasang sisi yang sama panjang dan sejajar, sisi yang berhadapan sama panjang.
2. Memiliki empat sudut yang sama besar yaitu 90^o
3. Memiliki dua diagonal sama panjang dan berpotongan tetapi tidak saling tegak lurus.
4. Banyaknya simetri putar adalah dua.
5. Memiliki dua simetri lipat.
6. Memiliki dua sumbu simetri
7. Rumus keliling persegi panjang: K = 2(panjang + lebar)
8. Rumus luas persegi panjang: L = panjang × lebar

Belah Ketupat

Karakteristik Belah Ketupat:

1. Mempunyai empat buah sisi dengan ukuran yang sama panjang dan empat buah titik sudut.
2. Besarmya sudut yang saling berhadapan adalah sama.
3. Diagonalnya saling berpotongan secara tegak lurus.
4. Banyaknya simetri lipat adalah dua buah.
5. Rumus keliling belah ketupat: K = 4×a
6. Rumus luas belah ketupat: L = ¹/₂× d₁ × d₂

Jajar genjang

Karakteristik jajar genjang:

1. Mempunyai dua pasang sisi yang sama panjang dan sejajar
2. Jumlah ke empat sudutnya adalah 360^o
3. Terdapat dua pasang sudut sama besar
4. Kedua diagonalnya berpotongan tetapi tidak sama panjang
5.  Rumus keliling jajar genjang: K = 2×(panjang + lebar) = 2 × (a + b)
6. Rumus luas jajar genjang: L = a × t

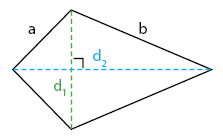
Layang-Layang

Karakteristik Layang-Layang:

1. Memiliki empat buah sisi dan empat buah titik sudut.
2. Memiliki dua pasang sisi yang ukurannya sama panjang.
3. Diagonalnya saling berpotongan dan tegak lurus.
4. Mempunyai dua buah sudut yang besarnya sama.
5. Banyaknya simetri lipat adalah 1 (satu) buah.
6. Rumus keliling layang-layang: K = 2×(a + b)
7. Rumus luas layang-layang: L = ¹/₂× d₁ × d₂

Trapesium

Karakteristik Trapesium:

1. Memiliki empat buah sisi dan titik sudut.
2. Besarnya sudut yang berada diantara sisi sejajar adalah 180^o.
3. Mempunyai sepasang sisi sejajar dengan ukuran yang tidak sama panjang (a dan c merupakan pasangan sisi sejajar.) 
4. Rumus keliling trapesium: K = a + b + c + d 
5. Rumus luas trapesium: L = ¹/₂× (a + c) × t_trapesium

Baca Juga: Kesebangunan pada Trapesium

Contoh Soal dan Pembahasan

Perhatikan gambar!

Luas daerah yang diarsir adalah ….
A.     15 cm²
B.     30 cm²
C.     45 cm²
D.     75 cm²

Pembahasan:

Mencari luas segitiga ABC:

Menghitung luas segitiga ABC:
L_ΔABC =  ¹/₂×AB×AC
L_ΔABC = ¹/₂×5×4 = 10 cm²

Mencari luas segitiga ABE:

Menghitung luas segitiga ABE:
L_ΔABE =  ¹/₂×AB×AE
L_ΔABC = ¹/₂×5×12 = 30 cm²

 Mencari luas segitiga ABD:

Menghitung luas segitiga ABD:
L_ΔABC =  ¹/₂×AB×AD
L_ΔABC = ¹/₂×5×8 = 20 cm²

Mencari luas yang diarsir:
L_arsir = L_ΔABE + L_ΔABD ‒ 2‒LΔABC
L_arsir = 30 + 20 ‒ 2‒10 = 50 ‒ 20 = 30 cm²
 
Jawaban: B

Sekian pembahasan karakteristik segi tiga dan segiempat. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Kesebangunan dan Kekongruenan