Pemfaktoran bentuk aljabar biasanya digunakan untuk menyederhanakan persamaan. Sebagai contoh 3xy + x yang dapat disederhanakan menjadi bentuk x(3y + 1). Contoh lainnya adalah x2 – 4x + 4 = (x – 2)2 dan x2 – 4 = (x – 2)(x + 2).
Lebih banyak mengenai pemfaktoran bentuk aljabar ada di bawah.
Daftar isi:
Baca Juga: Operasi Hitung Aljabar
Bentuk-Bentuk Pemfaktoran Aljabar
Bentuk pemfaktoran aljabar meliputi bentuk distributif, bentuk selisih kuadrat, bentuk kuadrat sempurna, bentuk x2 + bx + c = 0, dan bentuk ax2 + bx + c = 0 dengan nilai a ≠ 1. Beberapa bentuk persamaan umum aljabar dan hasil faktornya dapat disimak seperti pada ulasan di bawah.
1. Bentuk Distributif:
Sifat distributif pada pemfaktoran bentuk Aljabar:
- px + py = p(x + y)
- px ‒ py = p(x ‒ y)
Contoh:
3x + 3y = 3(x + y)
5x ‒ 5y = 5(x ‒ y)
2. Selisih Kuadrat:
Pemfaktoran selisih dari kuadrat dua bilangan: a2 ‒ b2 = (a + b)(a ‒ b)
Contoh:
Tentukan faktor dari 9x2 ‒ 16!
Dari persamaan 9x2 ‒ 16 dapat diperoleh bahwa a2 = 9x2 → a = 3x dan b2 = 16 → b = 4. Sehingga, 9x2 ‒ 16 = (3x)2 ‒ 42 = (3x + 4)(3x ‒ 4).
3. Kuadrat Sempurna:
Pemfaktoran persamaan kuadrat sempurna:
- x2 + 2xy + y2 = (x + y)(x + y)
x2 + 2xy + y2 = (x + y)2
- x2 ‒ 2xy + y2 = (x ‒ y)(x ‒ y)
x2 ‒ 2xy + y2 = (x ‒ y)2
Contoh:
x2 + 6x + 9 = (x + 3)2
x2 ‒ 6x + 9 = (x ‒ 3)2
4. Bentuk x2 + bx + c = 0:
Pemfaktoran persamaan kuadrat: x2 + bx +c = (x + p)(x+q) dengan nilai p + q = b dan p × q = c.
Contoh:
Faktorkan bentuk x2 ‒ 7x + 12 = 0!
Jawab:
Berdasarkan persamaan kuadrat x2 ‒ 7x + 12 = 0 dapat diketahui bahwa nilai a = 1, b = ‒7, dan c = 12
Untuk mendapatkan faktor persamaan kuadrat x2 ‒ 7x + 12 = 0 dapat dilakukan melalui beberapa langkah berikut.
Pertama, Cari bilangan p dan q yang memenuhi ketentuan berikut.
Hasil kali bilangan = 12
p × q = c
p × q = 12
Jumlah bilangan = ‒7
p + q = b
p + q = ‒7
Kemungkinan nilai p dan q yang memenuhi:

Diperoleh nilai p dan q yang memenuhi adalah p = ‒4 dan q= ‒3 (nilai p dan q tertukar tidak menjadi masalah). Jadi, hasil pemfaktoran yang benar adalah x2 ‒ 7x + 12 = (x ‒ 4)(x ‒ 3).
5. Bentuk ax2 + bx + c = 0 dengan a ≠1
Pemfaktoran persamaan kuadrat ax2 + bx +c adalah a( x +p/a)(x+q/a) dengan ketentukan nilai p + q = b dan p × q = ac.
Contoh:
Faktorkan persamaan kuadrat 2x2 ‒ 11x + 15!
Jawab:
Persamaan kuadrat 2x2 ‒ 11x + 15 memiliki nilai a = 2, b = ‒11, dan c = 15.
Cari bilangan p dan q yang memenuhi ketentuan berikut:
Hasil kali bilangan = 30
p × q = a × c
p × q = 2 × 15 = 30
Jumlah bilangan = ‒11
p + q = b
p + q = ‒11
Daftar nilai p dan q yang memenuhi:
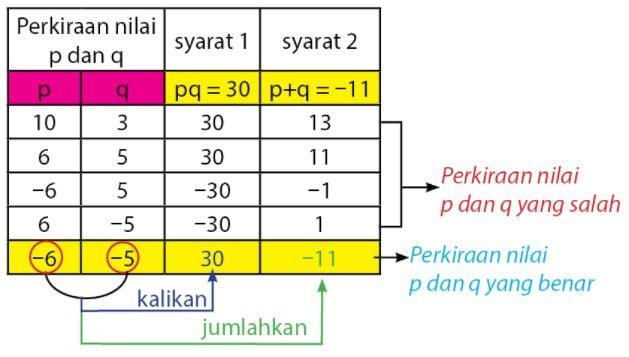
Nilai p dan q yang memenuhi adalah p = ‒5 dan q = ‒6, selanjutnya difaktorkan dengan cara berikut.
2x2 ‒ 11x + 15 = 2(x + (‒5/2))( x + (‒6/2))
= (2x + 2 × ‒5/2 )(x ‒ 3)
= (2x ‒ 5)(x ‒ 3)
Jadi hasil faktor untuk persamaan 2x2 ‒ 11x + 15 adalah (2x ‒ 5)(x ‒ 3).
Baca Juga: Grafik Fungsi Kuadrat
Contoh Soal dan Pembahasan
Beberapa soal pemfaktoran aljabar dan penyelesaiannya ada di bawah.
Contoh 1 – Soal pemfaktoran bentuk aljabar
Perhatikan pernyataan berikut!
I. 4x2 ‒ 9 = (2x + 3)(2x ‒ 3)
II. 2x2 + x ‒ 3 = (2x ‒ 3)(x + 1)
IIII. x2 + x ‒ 6 = (x + 3)(x ‒ 2)
IV. x2 + 4x ‒ 5 = (x ‒ 5)(x + 1)
Pernyataan yang benar adalah ….
A. I dan II
B. II dan III
C. I dan III
D. II dan IV
Pembahasan:
Menyelelidiki kebenaran dari persamaan I, II, III, dan IV.
Pernyataan I:
4x2 ‒ 9 = (2x)2 ‒ 32
4x2 ‒ 9 = (2x ‒ 3)(2x + 3) → Pernyataan I: Benar
Selidiki pernyataan II:
Dari persamaan kuadrat 2x2 + x ‒ 3 dapat diketahui bahwa nilai a = 2, b = 1, dan c = ‒3. Cari dua bilangan, misalkan p dan q, yang memenuhi ketentuan p × q = a × c = 2 × (‒3) = ‒6 dan p + q = b = 1.
Cari nilai p dan q yang memenuhi:
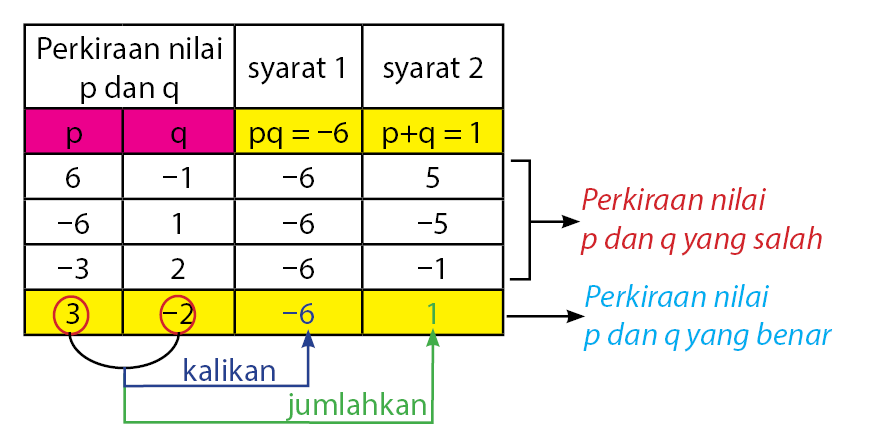
Diperoleh nilai p dan q yang memenuhi adalah p = 3 dan q = ‒2. Selanjutnya pemfaktoran aljabar dilakukan dengan cara berikut.
2x2 + x ‒ 3 = 2x2 ‒ 2x + 3x ‒ 3
= 2x(x ‒ 1) + 3(x ‒ 1)
= (2x + 3)(x ‒ 1) → Pernyataan II: Salah
Selidiki pernyataan III:
Persamaan kuadrat x2 + x ‒ 6 memiliki nilai a = 1, b = 1, dan c = ‒6. Pertama, cari dua bilangan, misalkan p dan q, yang memenuhi ketentuan p×q = c = ‒6 dan p+q = b = 1.
Sehingga,
x2 + x ‒ 6 = (x + 3)(x – 2) → Pernyataan II: Benar
Selidiki pernyataan IV:
Persamaan kuadrat x2 + 4x ‒ 5 memiliki nilai a = 1, b = 4 dan c = ‒5. Cari bilangan p dan q yang memenuhi ketentuan p×q = c = ‒5 dan p + q = b = 4.
Daftar nilai p dan q yang memenuhi:
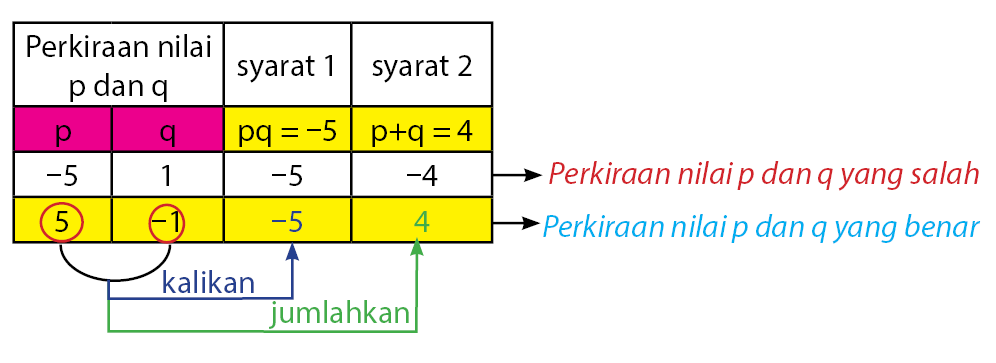
Nilai p dan q yang memenuhi adalah p = 5 dan q = ‒1. Sehingga x2 + 4x ‒ 5 = (x + 5)(x ‒ 1) → Pernyataan IV: Salah
Jadi, pernyatan yang benar adalah pernyataan I dan III.
Jawaban: C
Contoh 2 – Soal Pemfaktoran Bentuk Aljabar
Perhatikan pemfaktoran di bawah ini!
(i) 10x2 + 35x = 5x(2x + 7)
(ii) 49x2 – 36 = (7x + 12)(7x – 3)
(iii) x2 – 3x – 28 = (x – 7)(x – 4)
(iv) 3x2 – 16x – 35 = (3x + 5)(x – 7)
Pernyataan yang benar adalah ….
A. (i) dan (iii)
B. (i) dan (iv)
C. (ii) dan (iv)
D. (iii) dan (iv)
Pembahasan:
Menyelidiki kebenaran dari setiap pemfaktoran pada soal.
Pernyataan (i): Benar
10x2 + 35x = 5x × 2x + 5x × 7
10x2 + 35x = 5x(2x + 7)
Pernyataan (ii): Salah
49x2 ‒ 36 = (7x)2 ‒ 62
49x2 ‒ 36 = (7x ‒ 6)(7x + 6)
Pernyataan (iii): Salah
(x ‒ 7)(x ‒ 4) = x(x ‒ 4) ‒ 7 (x ‒ 4)
= x2 ‒ 4x ‒ 7x + 28
= x2 ‒ 11x + 28
Pernyataan (iv): Benar
(3x + 5)(x ‒ 7) = 3x(x ‒ 7) + 5(x ‒ 7)
= 3x2 ‒ 21x + 5x ‒ 35
= 3x2 ‒ 16x ‒ 35
Jadi, pernyataan yang benar terdapat pada nomor (i) dan (iv).
Jawaban: B
Demikianlah tadi penjelasan mengenai pemfaktoran aljabar dan contoh soalnya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Menyelesaikan Persamaan Kuadrat dengan TRIK KUCING
Fransiska sae
fransiskasae@gmail.com
101005