Rumus Persamaan Lingkaran Kelas 11 [Matematika SMA]

Rumus persamaan lingkaran menyatakan fungsi yang mebentuk grafik berupa lingkaran. Secara umum, persamaan lingkaran dengan titik pusat P(a, b) yang memiliki panjang jari-jari r adalah (x ‒ a)² + (y ‒ b)² = r². Sebagai contoh, persamaan lingkaran yang berpusat di titik P(2, ‒ 3) dengan jari-jari 5 satuan adalah (x ‒ 2)² + (y + 3)² = 25.

Perasamaan lingkaran (x ‒ 2)² + (y + 3)² = 25 dapat juga dinyatakan dalam bentuk penjabarannya yaitu x² + y² ‒ 4x + 6y ‒ 12 = 0. Hasil penjabaran tersebut merupakan bentuk umum persamaan lingkaran x² + y² + Ax ‒ By + C = 0.

Contoh lainnya, persamaan lingkaran dengan pusat O(0, 0) dan berjari-jari √5 adalah x² + y² = 5. Persamaan lingkaran tersebut diperoleh dari subtitusi nilai koordinat titik pusat O(a = 0, b = 0) dan jari-jari r = √5 pada rumus pesamaan lingkaran (x ‒ a)² + (y ‒ b)² = r².

Sehingga dapat disimpulkan bawaha ada tiga bentuk persamaan lingkaran yaitu x² + y² = r², (x ‒ a)² + (y ‒ b)² = r², dan x² + y² + Ax ‒ By + C = 0. Ketiga rumus tersebut memuat hubungan fungsi persamaan lingkaran dengan koordinat titik pusat dan panjang jari-jari lingkaran. Bagaimana penggunaan rumus persamaan lingkaran diulas lebih banyak di bawah.

Baca Juga: Kedudukan Antara 2 Lingkaran

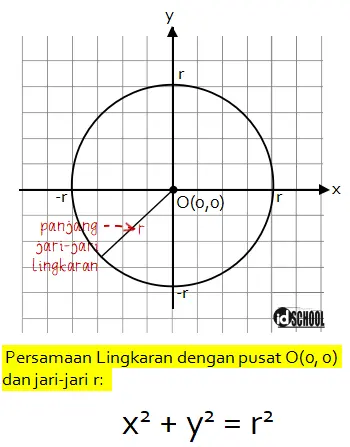
Lingkaran dengan Pusat O(0, 0) dan Jari-jari r

Sebuah lingkaran terletak pada bidang koordinat. Diketahui titik pusat dari lingkaran tersebut berada di titik O(0,0) dan panjang jari-jari r. Persamaan yang menyatakan grafik bentuk lingkaran tersebut adalah x² + y² = r².

Contoh:
Tentukan persamaan lingkaran yang berpusat di (0, 0) dan berjari-jari √2!

Jawab:
Diketahui titik pusat sebuah lingakran adalah O(0, 0) sehingga persamaannya dapat diketahui menggunakan rumus x² + y² = r².

Menentukan persamaan:
x² + y² = r²
x² + y² = (2√2)²
x² + y² = 2² × (√2)²
x² + y² = 4 × 2
x² + y² = 8

Diperoleh hasil akhir x² + y² = 8. Jadi persamaan yang tepat untuk menyatan sebuah lingkaran dengan titik pusat di O(0, 0) dan jari-jari r = 2√2 adalah x² + y² = 8.

Baca Juga: Persamaan Garis Singgung Lingkaran yang Diketahui Melalui Suatu Titik

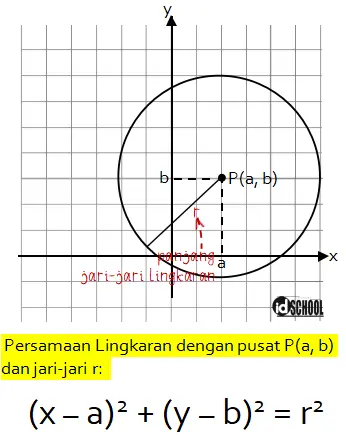
Lingkaran dengan Pusat P(a,b) dan Jari-jari r

Untuk sebuah lingkaran dengan titik pusat bukan pada titik O(0, 0) tidak bisa menggunakan rumus x² + y² = r². Misalnya pada sebuah lingkaran yang diketahui memiliki titik pusat P(a, b) dan jari-jari r. Rumus yang digunakan untuk menentukan persamaan lingkaran tersebut adalah (x − a)² + (y − b)² = r².

Contoh:
Tentukan persamaan lingkaran dengan pusat (-1, 2) dan jari-jari 3√2!

Jawab:
Titik pusat lingkaran bukan berada di titik (0, 0) melainkan di titik (-1, 2). Sehingga rumus yang dapat digunakan untuk menentukan lingkaran tersebut adalah

Misalkan, ebuah lingkaran diketahui memiliki titik pusat di P(−3, 1) dengan jari-jari 4 satuan. Persamaan lingkaran tersebut adalah (x + 3)² + (y − 1)² = 16.

Baca Juga: 3 Kedudukan Titik Terhadap Lingkaran

Bentuk Umum Persamaan Lingkaran

Bentuk umum persamaan lingkaran berikutnya merupakan penjabaran dari rumus lingkaran (x − a)² + (y − b)² = r². Bagaimana langkah penjabaran rumus lingkaran tersebut terdapat pada uraian berikut.

(x − a)² + (y − b)² = r²
x² − 2ax + a² + y² − 2by + b² = r²
x² + y² − 2ax − 2by + a² + b² − r² = 0

Untuk A = −2a; B = −2b; dan c = a² + b² − r² maka dapat diperoleh bentuk rumus x² + y² + Ax + By + C = 0. Sebuah lingkaran yang dinyatakan dalam bentuk persamaan x² + y² + Ax + By + C = 0 memiliki rumus pusat dan jari-jari lingkaran.

Bentuk umum persamaan lingkaran:

x² + y² + Ax + By + C = 0

Rumus pusat dan jari-jari lingkaran:

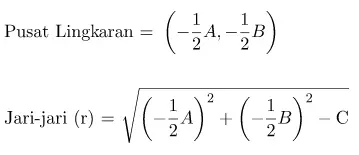
NOTE:
Jika diketahui pusat lingkaran adalah (x₁, y₁) dan garis singgung Ax + By + C = 0. Jari-jari lingkaran dapat dicari menggunakan rumus jarak titik ke garis (d) pada persamaan di bawah.

Contoh:
Tentukan jari-jari lingkaran x² + y² − 4x + 2y + c = 0 yang melalui titik A(5, −1)!

Jawab:
Pertama, perlu untuk mengetahui nilai c terlebih dahulu. Caranya dengan substitusi nilai titik koordinat (5, −1) pada persamaan x² + y² − 4x + 2y + c = 0.

Menentukan nilai c:
(5)² + (−1)² − 4(5) + 2(−1) + c = 0
25 + 1 − 20 − 2 + c = 0
4 + c = 0
c = −4

Diperoleh nilai c = −4 sehingga persamaan menjadi x² + y² − 4x + 2y − 4 = 0. Dari persamaan itu dapat diketahui nilai A = −4; B = 2; dan C = −4. Ketiga nilai tersebut dapat digunakan untuk mengetahui panjang jari-jari lingkaran tersebut.

Panjang jari-jari lingkaran:
r = √(¼A² + ¼B² ‒ C)
r = √(¼×(‒4)² + ¼×(2)² ‒ (‒4))
r = √(¼×16 + ¼×4 + 4)
r = √(4 + 2 + 4)
r = √10

Jadi, jari-jari lingkaran x² + y² − 4x + 2y + c = 0 yang melalui titik A(5, −1) adalah r = √10.

Baca Juga: Kedudukan Garis Terhadap Lingkaran

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah bahasan pemahaman di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Persamaan Lingkaran

Persamaan lingkaran yang sepusat dengan x² + y² + 6x − 4y − 3 = 0 dan melalui titik (2, 3) adalah ….
A. x² + y² + 6x − 4y − 13 = 0
B. x² + y² + 6x − 4y + 13 = 0
C. x² + y² − 4x + 6y − 23 = 0
D. x² + y² − 4x + 6y − 20 = 0
E. x² + y² + 4x − 6y + 23 = 0

Pembahasan:
Dari persamaan x² + y² + 6x − 4y − 3 = 0 dapat diketahui pusat dan jari-jari lingkaran.

Diketahui:
A = 6
B = −4
C = −3

Menentukan pusat lingkaran:
P(−¹/₂A, −¹/₂B)
= P(−¹/₂×6, −¹/₂×(−4))
= P( −3, 2)

Diketahui bahwa lingkaran melalui titik (2, 3). Jari-jari lingkaran sama dengan jarak antara pusat ke salah satu titik pada busur lingkaran. Sehingga, jari-jari lingkaran sama dengan jarak titik pusat P(−3, 2) ke titik (2, 3)

Menghitung kuadrat jari-jari lingkaran:
r² = (2 − (−3))² + (3 − 2)²
r² = 25 + 1
r² = 26

Diperoleh informasi bahwa lingkaran memiliki titik pusat P(−3, 2) dan kuadrat jari-jari r² = 26.

Menentukan persamaan lingkaran:
(x − (−3) )² + (y − 2)² = 26
(x + 3 )² + (y − 2)² = 26
x² + 6x + 9 + y² − 4y + 4 = 26
x² + y² + 6x − 4y − 13 = 0

Jadi, persamaan dari sebuah lingkaran yang sepusat dengan x² + y² + 6x − 4y − 3 = 0 dan melalui titik (2, 3) adalah x² + y² + 6x − 4y − 13 = 0.

Jawaban: A

Contoh 2 – Penggunaan Rumus Persamaan Lingkaran

Persamaan lingkaran yang berpusat di titik (−1, 2) dan menyinggung garis x + y + 7 = 0 adalah ….
A. x² + y² + 2x + 4y − 27 = 0
B. x² + y² + 2x − 4y − 27 = 0
C. x² + y² + 2x − 4y − 32 = 0
D. x² + y² − 4x − 2y − 32 = 0
E. x² + y² − 4x + 2y − 7 = 0

Pembahasan:
Berdasarkan infomasi yang diberikan pada soal dapat diperoleh gambaran lingkaran dan garis yang menyinggungnya seperti berikut.

Jari-jari lingkaran sama dengan jarak titik pusat pusat (−1, 2) ke garis x + y + 7 = 0. Sehingga, jari-jari lingkaran dapat dicari menggunakan rumus jarak titik ke garis seperti yang dilakukan pada langkah penyelesaian berikut.

Mencari persamaan untuk sebuah lingkaran yang diketahui memiliki titik pusat di (−1, 2) dan menyinggung garis x + y + 7 = 0:
(x + 1)² + (y − 2)² = 32
x² + 2x + 1 +y² − 4y + 4 = 32
x² + y² + 2x − 4y − 27 = 0

Jadi, persamaan dari sebuah lingkaran yang memiliki titik pusat (−1, 2) dan menyinggung garis x + y + 7 = 0 adalah x² + y² + 2x − 4y − 27 = 0.

Jawaban: B

Sekian ulasan mengenai rumus persamaan lingkaran, rumus pusat dan jari-jari lingkaran, serta contoh soal dan pembahasannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Persamaan dari Sebuah Lingkaran yang Dikeathui Melalui 3 Titik