Kesebangunan pada Segitiga Siku-Siku dan Contoh Soalnya

Dua buah segitiga dikatakan sebangun jika memiliki bentuk yang sama. Segitiga siku-siku memiliki rumus kesebanunan yang istimewa. Ada tiga rumus kesebangunan pada segitiga siku-siku yang perlu kamu ketahui.

Segitiga siku-siku adalah segitiga yang memiliki besar sudut 90^o pada salah satu sudutnya. Misalnya pada segitia siku-siku di titik B. Garis BD merupakan garis tinggi segitiga yang melalui titik B dan tegak lurus sisi AC. Ada tiga pasang segitga sebangun yaitu ΔADB ~ ΔBDC, ΔADB ~ ΔABC, dan ΔBDC ~ ΔABC.

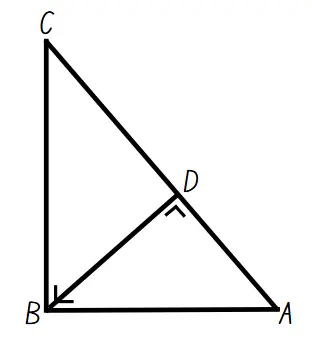
Lebih lanjut mengenai kesebangunan pada segitiga siku-siku ada di bawah.

Daftar isi:

• Rumus Kesebangunan pada Segitiga Siku-Siku
  • Bentuk I
  • Bentuk II
  • Bentuk III
• Contoh Soal Kesebangunan pada Segitiga Siku-Siku
  • Contoh 1
  • Contoh 2
  • Contoh 3

Rumus Kesebangunan pada Segitiga Siku-Siku

Ada tiga rumus kesebangunan pada segitiga siku-siku yang perlu diketahui. Ketiga rumus kesebangunan tersebut ada di bawah.

Bentuk I

Sebuah segitiga siku-siku ABC di titik B memiliki garis tinggi BD. Garis tinggi melewati titik B dan tegak lurus dengan sisi AC. Kuadrat panjang garis BC sama dengan perkalian panjang garis CA dan CD.

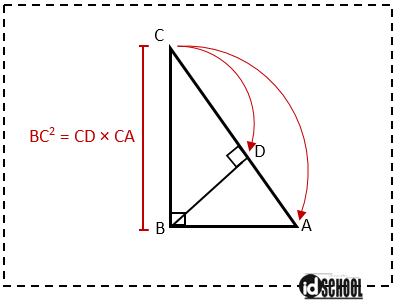
Persamaan BC² = CD × CA diperoleh dari kesebangunan segitiga ABC dan segitiga BDC. Perbandingan sisi BC dan DC sama dengan perbandingan sisi AC dan BC.

Sehingga,

*kalikan silang

BC × BC = CD × CA

BC² = CD × CA

Diperoleh rumus kesebangunan bentuk I yaitu BC² = CD × CA.

Bentuk II

Pada segitiga siku-siku ABC di titik B yang memiliki garis tinggi BD. Kuadrat panjang sisi BA sama dengan perkalian panjang sisi AD dan sisi AC.

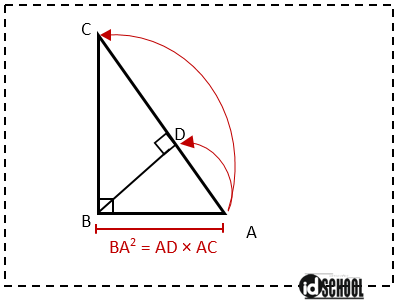
Rumus cepat kesebangunan untuk sisi AB adalah BA² = AD × AC. Rumus ini diperoleh dari kesebangunan pada segitiga ABC dan segitiga ABD.

Perbandingan panjang sisi AB dan AD sama dengan perbandingan sisi AC dan AB. Sehingga,

*kalikan silang

BA × BA = AD × AC

BA² = AD × AC

Diperoleh rumus kesebangunan bentuk II yaitu BA² = AD × AC.

Bentuk III

Sebuah segitiga siku-siku ABC di titik B memiliki garis tinggi BD. Kuadrat sisi BD sama dengan hasil kali panjang sisi AD dan panjang sisi CD.

Rumus cepat BD² = AD × AC diperoleh dari kesebangunan segitga ADB dan segitiga BDC. Perbandingan sisi DC dan BD sama dengan perbandingan sisi BD dan AC.

Sehingga,

*kalikan silang

BD × BD = AD × DC

BD² = AD × AC

Diperoleh rumus kesebangunan bentuk III yaitu BD² = AD × AC.

Ada tiga rumus cepat kesebangunan yang diperoleh. Ketiga rumusnya adalah BC² = CD × CA, BA² = AD × AC, dan BD² = AD × AC. Cara menggunakan rumusnya ada pada pembahasan contoh soal-soal di bawah.

Contoh Soal Kesebangunan pada Segitiga Siku-Siku

Soal di bawah dapat menambah pemahaman materi di atas.

Contoh 1

Perhatikan gambar!

Pada gambar tersebut, panjang KM adalah ….
A. 5√15
B. 5√10
C. 10√5
D. 15√5

Pembahasan:
Rumus kesebangunan yang digunakan untuk soal ini adalah bentuk I. Rumus cepat yang telah disesuaikan menjadi KM² = KN × KL.

Diketahui:
KN = 15 cm
KL = 15 + 10 = 25 cm

Menghitung panjang KM:

KM² = KN × KL

KM² = 15 × 25 = 375

Sehingga,

KM = √375

KM = √(25 × 15) = √25 × √15 = 5√15

Jadi, panjang KM adalah 5√15.

Jawaban: A

Contoh 2

Perhatikan gambar berikut!

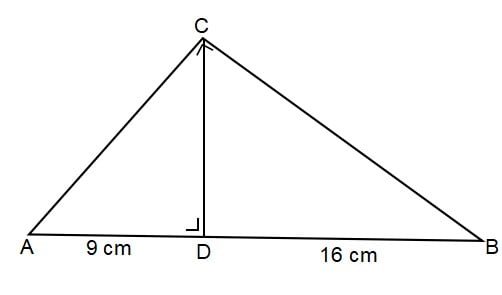
Panjang AC adalah ….
A. 12 cm
B. 14 cm
C. 15 cm
D. 20 cm

Pembahasan:
Rumus kesebangunan yang digunakan adalah rumus bentuk II. Rumus cepat yang sudah disesuaikan menjadi AC² = AD × AB.

Diketahui:
AD = 9 cm
AB = AD + DB = 9 + 16 = 25 cm

Menghitung panjang AC:

AC² = AD × AB

AC² = 9 × 25 = 225

Sehingga,
AC = √225 = 15 cm

Jadi, panjang AC adalah 15 cm.

Jawaban: C

Contoh 3

Perhatikan gambar berikut!

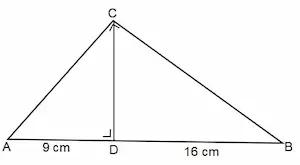
Jika panjang BD = 16 cm dan AD = 9 cm, panjang CD adalah … cm.
A. 8 cm
B. 10 cm
C. 12 cm
D. 14 cm

Pembahasan:
Soal contoh 3 ini dapat diselesaikan menggunakan rumus cepat kesebangunan bentuk III. Rumus cepat yang telah disesuaikan adalah CD² = AD × BD.

Diketahui:
AD = 9 cm
BD = 16 cm

Menghitung panjang CD:

CD² = AD × BD

CD² = 9 × 16 = 144

Sehingga,

CD = √144 = 12 cm

Jadi, panjang CD adalah 12 cm.

Jawaban: C

Demikianlah ulasan materi rumus kesebangunan pada segitiga siku-siku. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Kesebangunan dan Kekongruenan