Rumus Volume Kerucut dan Luas Permukaannya

Volume kerucut dapat dihitung mengguakan persamaan ¹/₃ volume tabung atau rumus volume kerucut sama dengan sepertiga Luas alas (L_alas) dikali tinggi kerucut (t_kerucut). Secara matemtais, besar volume kerucut sesuai dengan persamaan V_kerucut = ¹/₃ × L_alas × t_kerucut.

Diketahui bahwa alas kerucut berbentuk lingkaran (luas lingkaran L = π × r²) sehingga rumus volume kerucut sama dengan V_kerucut = ¹/₃ × π × r² × t_kerucut. Di mana r = adalah jari-jari lingkaran yang menjadi alas kerucut dengan π = ²²/₇ untuk kelipatan 7 atau π = 3,14 untuk r selain kelipatan 7.

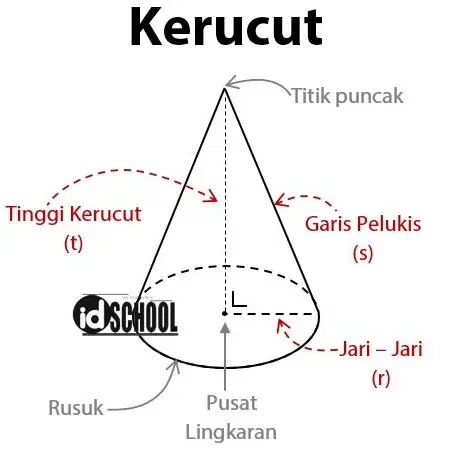
Kerucut memiliki dua buah sisi yaitu sisi alas dan selimut kerucut. Jumlah luas sisi alas dan selimut kerucut sama dengan luas permukaan kerucut seluruhnya. Luas lingkaran yang memiliki panjang jari-jari r pada alas kerucut dapat dihitung dengan rumus L_lingkaran = π × r². Sementara luas selimut kerucut dihitung dengan rumus L_{selimut kerucut} = π × r × s, di mana s adalah panjang garis pelukis kerucut.

Bagaimana cara menghitung besar volume kerucut? Bagaimana cara menghitung luas permukaan kerucut? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Baca Juga: Rumus Volume dan Luas Permukaan Limas

Bentuk Kerucut

Kerucut adalah bangun ruang sisi lengkung berupa limas dengan alas berbentuk lingkaran. Bidang sisi kerucut terdiri dari 2 buah sisi yaitu sisi alas dan sisi tegak. Bagian sisi alas berupa bentuk lingkaran penuh sedangkan pada sisi tegak kerucut merupakan selimut kerucut yang memiliki jaring-jaring berbentuk suatu bagian lingkaran.

Sisi alas kerucut berbentuk lingkaran sehingga luas alas kerucut sama dengan luas lingkaran. Sementara, selimut kerucut merupakan bagian lingkaran yang tidak utuh atau juring lingkaran.

Jika sebuah bangun kerucut dibuka maka akan terbentuk sebuah jaring-jaring kerucut yang terdiri dari sebuah lingkaran dan juring lingkaran.

Kerucut memiliki bagian-bagian penyusun yang terdiri dari titik sudut (titik puncak), garis pelukis (s), tinggi kerucut (t), dan jari-jari (r). Bagian-bagain kerucut sesuai dengan namanya ditunjukkan seperri keterangan gambar di bawah.

Baca Juga: Cara Hitung Luas Daerah yang Diarsir

Rumus Volume Kerucut

Volume kerucut adalah besar isi atau kapasitas yang dapat ditampung oleh bangun ruang berbentuk kerucut. Melalui percobaan sederhana dapat diketahui bahwa volume kerucut sama dengan ⅓ kali volume tabung untuk ukuran panjang dan tinggi yang sama.

Sobat idschool biasa mencoba membuktikan bahwa volume kerucut = ⅓volume tabung menggunakan kerucut dan tabung buatan sendiri. Bangun kerucut dapat dibuat melalui sebuah cara sederhana menggunakan bahan dan peralatan yang mudah ditemukan.

Setelah mempunyai bangun ruang berbentuk tabung dan kerucut, isi kerucut dengan tepung atau pasir kemudian tuang ke dalam tabung. Sobat idschool akan menjumpai bahwa tabung dapat terisi penuh ketika tiga takaran tepung/pasir dengan kerucut mengisi tabung.

Diketahui bahwa rumus volume tabung adalah V_tabung = π × r² × t_tabung, sehingga rumus volume kerucut sama dengan V_kerucut = ⅓V_tabung = ⅓ × π × r² × t_kerucut.

Baca Juga: Rumus Persentase Untung Rugi

Luas Permukaan Kerucut

Suatu kerucut dapat berbentuk kerucut tanpa alas atau kerucut dengan alas. Cara menghitung luas permukaan kerucut tanpa alas sedikit berbeda dengan luas permukaan kerucut dengan alas.

Pada kerucut tanpa alas, jaring-jaring kerucut hanya terdiri dari selimut kerucut yang berbentuk juring lingkaran. Sehingga luas permukaan kerucut tanpa alas sama dengan luas selimut kerucut.

Sementara pada kerucut dengan alas, jaring-jaring kerucut terdiri dari selimut kerucut dan lingkaran. Sehingga luas permukaan kerucut dengan alas sama dengan jumlah luas lingkaran dan selimut kerucut.

1) Kerucut Tanpa Alas (Luas Selimut Kerucut)

Rumus luas permukaan kerucut tanpa alas artinya hanya luas area yang disebut selimut kerucut. Bentuk selimut kerucut pada jaring-jarinng kerucut berupa juring lingkaran dengan jari-jari s. Untuk menghitung selimut kerucut, sobat idschool perlu mengetahui besar jari-jari lingkaran pada alas dan garis pelukis.

Rumus untuk menghitung selimut kerucut adalah hasil kali nilai π, jari-jari (r), dan garis pelukis (s).

Baca Juga: Karakteristik Segitiga dan Segi Empat

2) Kerucut Dengan Alas (Luas Kerucut Seluruhnya)

Luas permukaan kerucut dengan alas adalah luas area yang terdiri dari alas dan selimut kerucut. Rumus untuk menghitung selimut kerucut telah dibahas pada rumus luas permukaan kerucut tanpa alas di atas. Sehingga, untuk mengetahui besar luas permukaan kerucut dengan alas, sobat idschool cukup menambahkan luas alasnya.

Alas kerucut berbentuk lingkaran, persamaan yang dapat digunakan untuk menghitung luas lingkaran adalah hasil kali π dengan kuadrat jari-jari (L = πr²). Jadi, untuk mengetahui besar luas permukaan lingkaran dengan alas adalah menjumlahkan nilai πr² (luas lingkaran) dan πrs (luas selimut kerucut). Sehingga diperoleh rumus luas permukaan kerucut dengan alas yaitu L_kerucut = πr² + πr = πr(r + s).

Baca Juga: Macam – Macam Bangun Ruang Sisi Lengkung

Cara Menghitung Volume dan Luas Permukaan Kerucut

Sebuah kerucut diketahui memiliki panjang diamter alas 18 cm dan tingginya 12 cm, seperti kondisi yang ditunjukkan pada gambar berikut.

Tentukan:
a) volume kerucut
b) panjang garis pelukis kerucut
c) luas permukaan kerucut tanpa alas
d) luas permukaan kerucut

Penyelesaian:
Berdasarkan informasi pada soal diperoleh beberapa nilai ukuran seperti berikut:

• Diameter alas kerucut: d = 18 cm
  Jari-jari alas kerucut = r = d : 2 = 18 : 2 = 9 cm
• Tinggi kerucut: t = 12 cm

a) Menghitung volume kerucut:
V = ¹/₃ × π × r² × t
V = ¹/₃ × 3,14 × 9² × 12
V = ¹/₃ × 3,14 × 81 × 12
V = 1.017,36 cm³

b) Menghitung panjang garis pelukis kerucut (s):
Cara mencari garis pelukis kerucut dapat menggunakan Teorema Pythagoras seperti yang ditunjukkan pada cara berikut.

c) Menghitung luas permukaan kerucut tanpa alas:
L_{kerucut tanpa alas} = π × r × s
L = 3,14 × 9 × 15
L = 423,9 cm²

d) Menghitung luas permukaan kerucut:
L_{permukaan kerucut} = π × r (r + s)
L = 3,14 × 9 × (9 + 15)
L = 3,14 × 9 × 24 = 678,24 cm²

Baca Juga: Kesebangunan pada Segitiga

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Soal Volume Kerucut

Sebuah kerucut memiliki alas lingkaran dengan jari-jari 7 cm dan tingginya 24 cm. Volume kerucut tersebut adalah …. (π = ²²/₇)
A. 3.696 cm³
B. 2.464 cm³
C. 1.232 cm³
D. 616 cm³

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh beberapa informasi seperti berikut.

• jari-jari alas kerucut: r = 7 cm
• tinggi kerucut: t = 24 cm

Menghitung volume kerucut:

Jadi, volume kerucut tersebut adalah 1.232 cm³.

Jawaban: C

Contoh 2 – Penggunaan Luas Permukaan Kerucut

Perhatikan gambar berikut!

Tutup lampu berbentuk kerucut terpotong seperti gambar di atas. Luas minimum bahan yg diperlukan untuk membuat lampu tersebut adalah ….
A.120π cm²
B.105π cm²
C.90π cm²
D.60π cm²​

Pembahasan:
Luas minimum bahan yg diperlukan untuk membuat tutup lampu tersebut dapat diperoleh dengan menghitung luas permukaan bangun. Perhatikan kembali bentuk tutup lampu seperti yang diberikan pada soal dengan sedikit garis bantu berikut.

Diketahui:

• Jari-jari kerucut besar: r_b = 9 cm
• Jari-jari kerucut kecil: r_k = 3 cm
• Luas tutup lampu sama dengan luas permukaan kerucut besar dikurangi luas permukaan kerucut kecil.

Menghitung nilai x (gunakan persamaan pada perbandingan senilai):
³/₉ = ^x/_{10 + x}
3(10 + x) = 9x
30 + 3x = 9 x
9 x – 3x = 30
6x = 30
x = ³⁰/₆ = 5 cm

Sehingga dapat diperoleh panjang garis kerucut besar dan kecil:

• Garis pelukis kerucut kecil: s_k = x = 5 cm
• Garis pelukis kerucut besar: s_b = 10 + x = 10 + 5 = 15 cm

Menghitung besar luas selimut kerucut besar:
L_b = π × r_b × s_b
= π × 9 × 15
= 135π cm²

Menghitung besar luas selimut kerucut kecil:
L_k= π × r_k × s_k
= π × 3 × 5
= 15π cm²

Menghitung luas minimum L_min = L_b – L_k
= 135π cm²– 15π cm²
= 120π cm²

Jadi, luas permukaan tutup lampu dapat menggunakan bahan minimum sebesar 120π cm².

Jawaban: A

Itulah tadi bahasan mengenai bangun ruang sisi lengkung pada kerucut yang meliputi bahasan rumus luas permukaan dan rumus volume kerucut. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Unsur – Unsur, Keliling, dan Luas Lingkaran