Teorema pythagoras menyatakan hubungan antara ketiga sisi yang terdapat pada segitiga siku-siku. Rumus teorema Pythagoras memiliki bentuk persamaan matematis c2 = a2 + b2. Di mana rumus teorema pythagoras tersebut berlaku pada segitiga siku-siku ABC dengan letak sudut siku-siku di titik C.
Teorema pythagoras sudah diperkenalkan di bangku SD. Penggunaan Teorema Pythagoras masih ditemukan di tingkat yang lebih lanjut seperti SMP, SMA, dan tingkatan yang lebih lanjut.
Tiga bilangan yang memenuhi Teorema Pythagoras disebut tripel pythagoras. Ketiga bilangan dalam tripel Pythagoras dapat digunakan untuk mempermudah perhitungan.
Bagiamana penggunana rumus Teorema Pythagoras? Bagaimana bentuk tripel Pythagoras? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar Isi:
Rumus Teorema Pythagoras
Teorema pythagoras hanya berlaku untuk segitiga yang memiliki satu sudut siku-siku (besar sudut 90o). Bunyi teorema pythagoras mengatakan bahwa pada segitiga siku-siku berlaku kuadrat sisi miring sama dengan jumlah kuadrat kedua sisi penyikunya.
Sisi miring atau hipotenusa terletak di depan sudut siku-siku. Panjang sisi miring dalam segitiga siku-siku adalah yang terpanjang.

Misalkan diketahui segitiga ABC siku-siku di C. Tiga sisi pada segitiga ABC adalah sisi AB = c, sisi BC = a, dan sisi AC = b.
Sisi miring atau hipotenusa dari segitiga ABC tersebut adalah sisi AB.
Ada tiga rumus Teorema Pythagoras yang berlaku pada segitiga ABC yaitu c2 = a2 + b2; b2 = c2 ‒ a2
; dan a2 = c2 ‒ b2.

Selain segitiga siku-siku, ada 2 jenis segitiga lain berdasarkan besar sudutnya. Dua jenis segitiga lainnya adalah segitiga lancip dan segitiga tumpul.
Pada segitiga siku-siku memiliki karakteristik jika kuadrat sisi miring sama dengan (=) jumlah kuadrat sisi yang lain. Sementara untuk segitiga lancip dan tumpul memenuhi karakteristik berikut.
- Jika kuadrat sisi miring < jumlah kuadrat sisi yang lain, maka segitiga tersebut adalah segitiga lancip.
- Jika kuadrat sisi miring > jumlah kuadrat sisi yang lain, maka segitiga tersebut adalah segitiga tumpul.
Sehingga dari persamaan dalam Teorema Pythagoras juga dapat diselidiki apakah segitiga termasuk segitiga lancip atau tumpul.
Baca Juga: Karakteristik Segitiga
Tripel Pythagoras
Tripel pythagoras adalah kumpulan tiga bilangan yang memenuhi teorema pythagras. Contoh tiga bilangan yang meruapakan tripel Pythagoras adalah 3, 4, dan 5.
Bilangan 3, 4, dan 5 memenuhi teorema pythagoras yaitu 32 + 42 = 9 + 16 = 25 = 52. Kelipatan dari tiga bilangan 3, 4, dan 5 juga merupakan tipel Pythagoras, seperti 6, 8, dan 10.
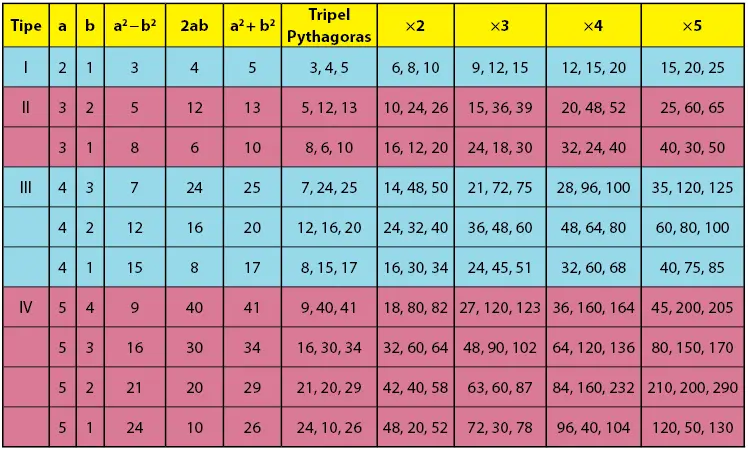
Untuk mendapatkan tiga bilangan ini dapat menggunakan rumus. Setidaknya ada empat tipe bentuk tripel pythagoras yang akan diulas di sini.
Empat bentuk tipe pythagoras tersebut dapat menghasilkan puluhan, bahkan ratusan bilangan tripel pythagoras.
Cara menentukan 3 bilangan Tripel Pythagoras:
Jika a dan b bilangan bulat positif dan a > b, maka tripel pythagoras dapat disusun menggunakan memenuhi persamaan tiga bilangan 2ab, a2 – b2, a2 + b2
Kumpulan empat bentuk bilangan Tripel Pythagoras terdapat pada tabel berikut.
Baca Juga: Perbandingan Sisi dan Sudut pada Segitiga Siku-Siku dengan Sudut Istimewa
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Jarak Patok
Sebuah tiang tingginya 12 m berdiri tegak di atas tanah datar. Dari ujung atas tiang ditarik seutas tali ke sebuah patok pada tanah. Jika panjang tali 15 m, maka jarak patok dengan pangkal tiang bagian bawah adalah ….
A. 13,5 m
B. 10 m
C. 9 m
D. 3 m
Pembahasan:
Gambar di bawah sesuai dengan informasi yang diberikan pada soal.

Gunakan teorema Pythagoras untuk mencari jarak patok dengan pangkal tiang bagian bawah. Jarak patok dengan pangkal tiang bagian bawah dapat dihitung seperti cara berikut.
Jarak patok (Jp):
Jp2 = 152 ‒ 122
Jp2 = 225 ‒ 144 = 81
Jp = √81 = 9 m
Jadi, jarak patok dengan pangkal tiang bagian bawah adalah 9 m.
Jawaban: C
Contoh 2 – Soal Jarak Terpendek
Sebuah kapal berlayar sejauh 100 km ke arah barat, kemudian berbelok ke arah selatan sejauh 75 km. Jarak terpendek kapal tersebut dari titik keberangkatan adalah ….
A. 75 km
B. 100 km
C. 125 km
D. 175 km
Pembahasan:
Soal cerita diatas dapat digambar seperti gambar berikut.
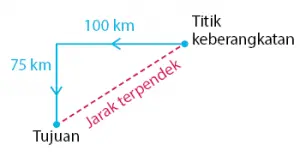
Jarak terpendek kapal tersebut (d) dari titik keberangkatan dapat dihitung seperti cara berikut.
d2 = 1002 + 752
d2 = 10.000 + 5.625 = 15.625
d = √15.625 = 125 km
Jadi, jarak terpendek kapal tersebut dari titik keberangkatan adalah 125 km.
Jawaban: C
Sekian pembahasan mengenai rumus Teorema Pythagoras beserta empat bentuk tripel Pythagoras. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Rumus Trapesium untuk Menghitung Keliling (K) dan Luas (L)