Selain membutuhkan rumus integral trigonometri, pengerjaan soal integral dari fungsi-fungsi trigonometri teknik/metode. Di mana ada dua metode yang dapat digunakan yaitu metode integral substitusi dan integral parsial. Kedua metode tersebut juga digunakan untuk menentukan hasil integral dari fungsi yang bukan merupakan fungsi trigonometri.
Bentuk dasar dari rumus integral trigoometri adalah hasil integral dari fungsi-fungsi trigonometri dasar. Rumus-rumus tersebut diperoleh dari definisi integral.
Beberapa persamaan dalam rumus integral trigonometri sesuai diberikan seperti berikut.

Rumus integral trigonometri yang diberikan di atas dapat selalu membantuk dan dibutuhkan untuk untuk menentukan hasil integral dari fungsi trigonometri yang lebih kompleks/rumit. Jadi, sebaiknya sobat idschool sudah memahami persamaan dasar dari rumus integral trigonometri tersebut.
Bagaimana cara menentukan hasil intgral dari fungsi trigonometri? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Penggunaan Rumus Integral Trigonometri
Selain rumus integral fungsi trigonometri baku yang telah diulas di atas, ada satu bagian lagi yang cukup penting untuk menyelesaikan soal integral fungsi trigonometri yaitu identitas terigonometri. Beberapa soal membutuhkan identitas fungsi trigonometri agar menjadi bentuk yang lebih mudah untuk dikerjakan.
Selanjutnya, bentuk soal integral trigonometri dapat diselesaikan dengan metode substitusi dan metode integral parsial. Penggunaan metode yang mana, disesuaikan dengan bentuk soal yang diberikan.
Bentuk soal integral trigonometri yang diselesaikan dengan metode substitusi
Berikut ini adalah contoh soal integral trigonometri yang dapat diselesaikan menggunakan metode substitusi.
Soal Integral Trigonometri #1:

Penyelesaian:
Misalkan: u = 2x + 5 maka du = 2 dx → dx = du/2, hasil integral dari soal integral trigonometri #1 dapat diselesaikan seperti pada cara berikut.
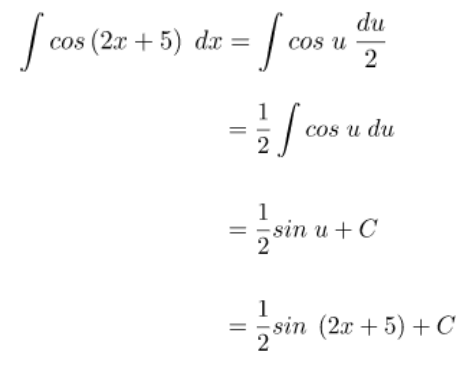
Bentuk soal integral trigonometri yang diselesaikan dengan metode integral parsial
Sebagai bahan untuk menambah pemahaman sobat idschool mengenai rumus integral trigonometri, berikut ini akan diberikan contoh soal integral fungsi trigonometri. Simak beberapa contoh soal dan pembahasannya di bawah.
Soal Integral Trigonometri #2: Apa hasil integral yang tepat untuk fungsi trigonometri di bawah?

Penyelesaian:
Soal integral trigonometri #2 dapat diselesaikan dengan mengubah menggunakan identitas trigonometri kemudian baru mencari hasil integralnya. Penyelesaian dari bentuk integral trigonometri tersebut dapat dilakukan seperti pada cara di bawah.

Soal Integral Trigonometri #3:
Tentukan hasil integral dari fungsi trigonometri di bawah!

Penyelesaian:
Soal yang diberikan dapat diselesaikan langsung menggunakan rumus baku fungsi integral trigonometri yang diberikan ulasan pada bagian atas sebelumnya.
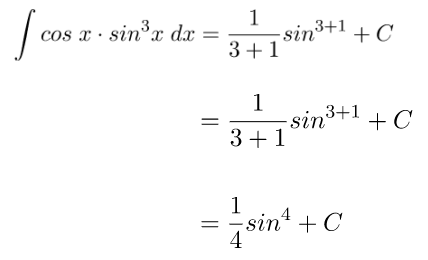
Soal Integral Trigonometri #4:
Tentukan hasil integral dari fungsi trigonometri di bawah!

Penyelesaian:
Hasil dari soal integral trigonometri #4 dapat diperoleh melalui langkah-langkah pengerjaan seperti cara berikut.
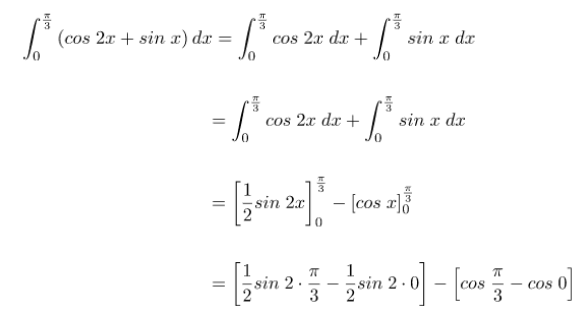
Dengan subtitusi nilai fungsi trigonometri yang sesuai maka akan diperoleh nilai hasil intergal dari soal integral trigonometri #4.

Sekian pembahasan rumus integral trignometri yang dapat diselesaikan dengan dua metode yaitu integral trigonometri substitusi dan parsil. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Kenali Berbagai Bentuk Soal Integral, Gunakan Metode Integral yang Tepat untuk Menyelesaikannya!