Cara Melengkapi Tabel Kebenaran dalam Logika Matematika

Cara melengkapi tabel kebenaran dilakukan dengan menyesuaikan aturan bernalar dari operator logika matematika. Tabel kebenaran adalah sebuah tabel yang memuat semua nilai kebenaran dari kombinasi nilai-nilai kebenaran suatu preposisi. Preposisi merupakan pernyataan yang dapat bernilai benar (true) atau salah (false), tetapi tidak dapat bernilai keduanya.

Nilai kebenaran untuk preposisi tunggal atau atomik cukup mudah dilakukan, contohnya pada preposisi: Bulan dapat memancarkan cahaya sendiri. Contoh preposisi tunggal tersebut memiliki nilai kebenaran salah atau false karena bulan tidak mempunyai cahaya sendiri.

Sementara untuk preposisi majemuk yang memiliki lebih dari satu preposisi tunggal memiliki nilai kebenaran yang membutuhkan analisis terlebih dahulu. Cara melakukan analisis nilia kebenaran untuk preposisi majemuk menyesuaikan aturan operator logika yang berlaku.

Ada empat operator logika matematika yaitu konjungsi (dan), disjungsi (atau), implikasi (jika … maka …), dan biimplikasi (… jika dan hanya jika …). Aturan penalaran pada logika matematika untuk konjungsi, disjungsi, implikasi, dan biimplikasi sesuai dengan nilai-nilai kebenaran pada empat tabel berikut.

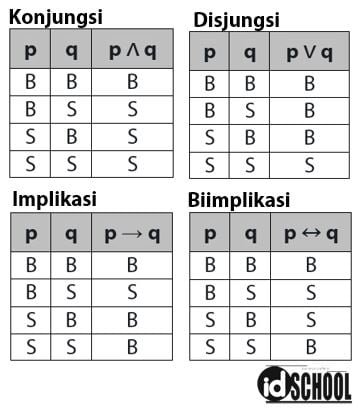
Baca Juga: Logika Matematika (Konjungsi, Disjungsi, Implikasi, dan Biimplikasi)

Aturan penalaran untuk empat operator logika matematika seperti pada empat tabel di atas berguna pada cara melengkapi tabel kebenaran. Bagaimana cara melengkapi tabel kebenaran dalam logika matematika? Sobat idschool dapat mencari tahu cara melengkapi tabel kebenaran dalam logika matematika melalui ulasan di bawah.

Table of Contents

• Penyataan, Proposisi, dan Nilai Kebenaran
• Langkah – Langkah Melengkapi Tabel Kebenaran
• Contoh Cara Melengkapi Tabel Kebenaran
  • Contoh 1 – Melengkapi Tabel Kebenaran untuk 2 Proposisi Tunggal
  • Contoh 2 – Melengkapi Tabel Kebenaran untuk 3 Proposisi Tunggal

Penyataan, Proposisi, dan Nilai Kebenaran

Sebuah pernyataan dapat termasuk sebagai preposisi atau bukan proposisi. Setiap preposisi merupakan pernyataan, namun setiap pernyataan belum tentu merupakan preposisi. Preposisi merupakan pernyataan yang dapat memiliki nilai kebanaran benar atau salah.

Sebagai contoh proposisi dengan nilai kebenaran benar adalah Indonesia adalah nama sebuah negara. Diketahui secara umum bahwa Indonesia merupakan sebuah nama negara yang merdeka sejak 17 Agustus 1945. Jadi, contoh kalimat tersebut merupakan sebuah pernyatataan sekaligus preposisi dengan nilai kebenaran benar.

Untuk contoh preposisi dengan nilai kebenaran salah adalah Bilangan prima terkecil adalah satu. Diketahui bahwa bilangan prima terkecil adalah dua. Sehingga pernyataan tersebut merupakan preposisi dengan nilai kebenaran salah.

Selanjutnya perhatikan contoh pernyataan: Sebuah bilangan asli memiliki nilai lebih besar dari 5. Pernyataan tersebut akan bernilai benar jika bilangan yang dimaksud adalah 1, 2, 3, dan 4. Namun pernyataan tersebut akan bernilai salah jika bilangan yang dimaksud adalah 6, 7, 8, 9, dan seterusnya. Contoh pernyataan tersebut bukan preposisi karena dapat memiliki dua nilai kebenaran.

Baca Juga: Kalimat Terbuka dan Tertutup dalam Matematika

Tabel kebenaran dalam logika matematika memuat kombinasi nilai-nilai kebenaran dari suatu preposisi majemuk. Bahasan bagaimana cara melangkapi tabel kebenaran dalam logika matematika untuk preposisi majemuk akan menjadi pembahasan berikutnya.

Langkah – Langkah Melengkapi Tabel Kebenaran

Nilai kebenaran dari preposisi majemuk ditentukan oleh nilai kebenaran dari preposisi tunggalnya. Hasil dari nilai kebenaran dari preposisi majemuk mengikuti aturan penalaran pada operator logika yang digunakan.

Operator logika yang digunakan dapat berupa konjungsi (∧), disjungsi (∨), implikasi (→), atau biimplikasi (↔). Untuk itu perlu mengingat kembali aturan penalaran menentukan nilai kebenaran yang berlaku untuk keempat operator logika tersebut.

Aturan penalaran untuk empat operator logika dirangkum seperti berikut:

1. Konjungsi akan bernilai benar jika semua pernyataan bernilai benar, selain itu salah
2. Disjungsi akan bernilai benar jika ada salah satu penyataan bernilai benar
3. Implikasi akan bernilai salah jika anteseden (sebab/alasan/hipotesa) bernilai benar dan konsekuen (akibat/kesimpulan/konklusi) bernilai salah, selain itu bernilai benar
4. Biimplikasi hanya akan bernilai benar jika anteseden dan konsukeun memiliki nilai kebenaran yang sama

Tingkat kekuatan operator logika atau kata penghubung dalam logika matematika dari yang lemah ke kuat berturut – turut adalah negasi (ingkaran), konjungsi/disjungsi, implikasi, dan biimplikasi.

Penentuan nilai kebenaran dimulai dari operator yang lemah ke operator yang lebih kuat. Namun jika terdapat proposisi majemuk dalam tanda kurung dikerjakan terlebih dahulu.

Ada beberapa tahapan yang perlu dilakukan untuk melengkapi tabel kebenaran. Secara singkat, langkah – langkah melengkapi tabel kebenaran diberikan seperti berikut.

1. Buat tabel dengan ukuran menyesuaikan proposisi majemuk yang diberikan
2. Isi tabel pernyataan dengan kombinasi nilai kebenaran benar dan salah
3. Lengkapi tabel sesuai dengan aturan penalaran pada operator logika

Baca Juga: Cara Menentukan Domain, Kodomain, dan Range

Selanjutnya, simak bagaimana cara melengkapi tabel kebenaran dalam logika matematika di bawah untuk menambah pemahaman sobat idschool.

Contoh Cara Melengkapi Tabel Kebenaran

Contoh cara melengkapi tabel kebenaran di bawah akan diberikan dalam dua contoh soal. Pertama adalah contoh yang melibatkan dua preposisi, dan kedua adalah contoh yang melibatkan tiga preposisi. Cara melengkapi tabel kebenaran dalam logika matematika secara lebih jelas diberikan seperti penyelesaian di bawah.

Contoh 1 – Melengkapi Tabel Kebenaran untuk 2 Proposisi Tunggal

Buatlah tabel kebenaran dari ekspresi logika: p → q ↔ p ∧ ~q

Pertama, pisahkan satu persatu proposisi majemuk berdasarkan operator logika. Hasil untuk contoh soal di atas adalah sebagai berikut.

• p → q
• p ∧ ~q
• p → q ↔ p ∧ ~q

Kolom yang dibutuhkan untuk membuat tabel kebenaran pada ekspresi logika di atas meliputi kolom p, q, ~q, p → q, p ∧ ~q, dan p → q ↔ p ∧ ~q (ada 6 kolom). Banyaknya proposi tunggal ada 2 sehingga banyaknya kombinasi nilai kebenaran ada sebanyak 2² = 4. Jadi, banyak baris yang dibutuhkan adalah 4 baris + 1 kolom untuk ekspresi logika.

Bentuk kolom tersebut menjadi seperti yang terlihat di bawah.

Selanjutnya sobat idschool perlu melengkapi kolom tabel kebenaran satu persatu. Mulai dari kolom paling kiri.

1. Negasi q atau ~q mempunyai nilai kebenaran yang berkebalikan dengan nilai kebenaran q. Untuk melengkapi nilai kebenaran pada kolom ~q, sobat idschool hanya perlu memperhatikan kolom q. Hasil nilai kebenaran untuk mengisi kolom ~q berturut – turut adalah S, B, S, B.

2. Implikasi akan bernilai salah jika anteseden (p) bernilai benar dan konsekuen (q) bernilai salah, selain itu nilaninya benar. Untuk melengkapi nilai kebenaran pada kolom ini perlu memperhatikan dua kolom, p dan q. Nilai kebenaran untuk mengisi kolom p → beruturut – turut adalah B, S, B, B

3. Berikutnya melengkapi nilai kebenaran pada kolom p ∧ ~q. Konjungsi hanya akan bernilai benar jika kedua pernyataan bernilai benar. Untuk melengkapi kolom ini, perhatikan kolom p dan ~q. Hasil nilai kebenaran untuk kolom p ∧ ~q berturut – turut adalah S, B, S, S.

4. Langkah terakhir adalah melengkapi kolom untuk ekspresi logika p → q ↔ p ∧ ~q. Suatu biimplikasi (↔) hanya akan bernilai benar jika anteseden dan konsekuen memiliki nilai kebenaran yang sama. Untuk melengkapi kolom p → q ↔ p ∧ ~q perlu meperhatikan dua kolom yaitu p → q dan p ∧ ~q. Hasil nilai kebenaran untuk biimplikasi p → q dan p ∧ ~q berturut – turut adalah S, S, S, S.

Sampai di sini, sobat idschool sudah menyelesaikan cara melengkapi tabel kebenaran dalam logika matematika. Hasil pada langkah – langkah di atas dapat terlihat jelas seperti pada cara melengkapi tabel kebenaran berikut.

Baca Juga: Cara Menentukan Banyak Pemetaan

Contoh 2 – Melengkapi Tabel Kebenaran untuk 3 Proposisi Tunggal

Buatlah tabel kebenaran untuk ekspresi logika: [(p→q) ∧ (~q ∨ r)] → (p→r)

Banyaknya proposi tunggal ada 3 sehingga banyaknya kombinasi nilai kebenaran ada sebanyak 2³ = 8. Jadi, banyak baris yang dibutuhkan adalah 8 baris + 1 kolom untuk ekspresi logika.

Kolom yang dibutuhkan untuk membuat tabel kebenaran pada ekspresi logika di atas meliputi kolom p, q, r, (p→q), (~q ∨ r), p→r, (p→q) ∧ (~q ∨ r), dan [(p→q) ∧ (~q ∨ r)]→(p→r). Banyaknya kolom yang dibutuhkan adalah sebanyak 8 kolom.

Bentuk tabel kebenaran yang dibutuhkan untuk ekspresi logika pada contoh dapat terlihat seperti berikut.

Selanjutnya sobat idschool hanya perlu mengisi tabel kebenaran yang kosong tersebut sesuai aturan pada operator logika matematika. Dengan mengikuti langkah seperti cara melengkapi tabel kebenaran pada contoh sebelumnya akan tersisi semua nilai kebenaran untuk tabel di atas.

Hasil dari cara melengkapi tabel kebenaran dalam logika matematika untuk tabel kebenaran dengan ekspresi logika [(p→q) ∧ (~q ∨ r)]→(p→r) sesuai dengan tabel di bawah.

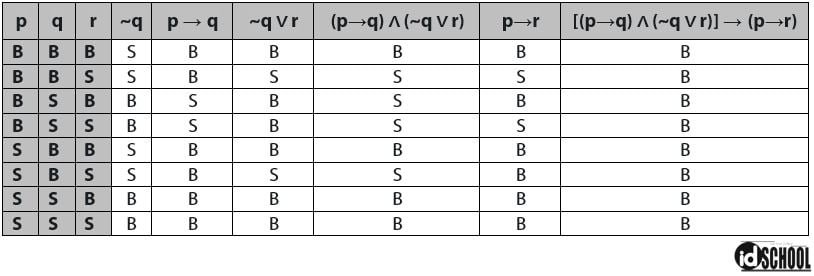
Sekian ulasan materi cara melengkapi tabel kebenaran dalam logika matematika. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Pola Bilangan dan Rumus Un Untuk Pola Bilangan