Logika matematika adalah bahasan ilmu matematika mengenai bagaimana penalaran atau cara berpikir. Bahasan materi logika matematika meliputi cara menentukan penalaran yang tepat dengan penalaran yang tidak tepat. Materi didalamnya berkaitan dengan pemecahan masalah pernyataan majemuk dan berkuantor.
Pernyataan majemuk dalam materi logika matematika dihubungkan dalam empat kata penghubung yang berbeda. Empat kata hubung tersebut meliputi konjungsi (∧), disjungsi (∨), implikasi (→), dan biimplikasi (↔) yang biasa disebut sebagai operator logika. Setiap operator logika matematika memiliki aturan penalaran yang berbeda,
Sementara penyataan berkuantor adalah pernyataan yang mengandung ukuran kuantitas atau jumlah seperti kata semua, setiap, beberapa, ada, dan lain sebagainya. Ada dua jenis macam kuantor yaitu kuantor universal (∀) dan kuantor eksistensial (∃). Kuantor universal meliputi ukuran kuantitas semua, setiap, dan sejenisnya. Sedangkan kuantor eksisrensial meliputi ukuran kuantitas beberapa, sebagian, ada, dan lain sebagainya.
Bagaimana aturan bernalar dalam logika matematika? Bagaimana cara menggunakan operator logika matemtika? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Penyataan atau Preposisi
Sebelumnya, kenali dulu sebuah kalimat untuk sebuah pernyataan yang disebut proposisi. Suatu preposisi adalah pernyataan yang memiliki nilai kebenaran benar atau salah namun tidak dapat bernilai benar dan salah.
Pernyataan yang sudah dapat diketahui kebenarannya dalam matematika disebut kalimat tertutup. Sedangkan pernyataan yang belum diketahui nilai kebenarannya disebut kalimat terbuka.
Pernyataan majemuk adalah beberapa preposisi yang dipisahkan oleh kata penghubung dalam operator logika matematika. Empat operator logika matematika terdiri dari dan, atau, jika … maka…, serta jika dan hanya jika.

Baca Juga: Kalimat Terbuka dan Tertutup dalam Matematika
Kata penghubung dan dalam logika matematika disebut konjungsi (∧), sedangkan untuk kata penghubung atau disebut disjungsi (∨). Kata penghubung … jika … maka … dan … jika dan hanya jika … berturut – turut disebut implikasi (→) dan biimplikasi (↔).
Kebenaran atau kesalahan dari sebuah pernyataan atau preposisi disebut nilai kebenarannya (truth value). Contoh pernyataan dengan nilai kebenaran true/benar adalah Ir. H. Joko Widodo adalah presiden ke – 7 Indonesia.
Pernyataan memiliki negasi dengan nilai kebenaran yang berkebalikan, biasanya pernyataan negasi memiliki penambahan kata tidak atau bukan. Negasi dari contoh pernyataan yang bernilai salah adalah Ir. H. Joko Widodo bukan presiden ke – 7 Indonesia.
Negasi disimbolkan dengan tanda ∼, sehingga nagasi dari pernyataan p adalah ∼p. Nilai kebenaran untuk preposisi dan ingkarannya akan selalu berkebalikan. Jika p bernilai benar maka ~p bernilai salah, sebaliknya jika p bernilai salah maka ~p bernilai benar.
4 Operator Logika Matematika
Bagaimana aturan penalaran untuk empat operator logika matematika akan diulas banyak melalui masing-masing bahasan di bawah
1) Konjungsi (p ∧ q)
Konjungsi merupakan pernyataan majemuk dengan kata penghubung dan (simbol: ∧). Selain kata dan, kata penghubung yang bisa digunakan meliputi tetapi, ketika, seandainya, seperti, bahwa, walaupun, supaya.
Nilai kebenaran dari sebuah konjungsi akan bernilai benar jika semua pernyataannya bernilai benar, selain itu nilai kebenaran konjungsi akan salah. Tabel kebenaran untuk konjungsi sebagai operator logika matematika dengan dua preposisi sesuai pada kondisi berikut.

Tabel kebenaran konjungsi untuk tiga pernyataan diberikan seperti berikut.

Contoh konjungsi yang bernilai benar: Hasil dari 3 + 6 adalah 9 dan 9 merupakan bilangan ganjil.
- Pernyataan pertama yaitu Hasil dari 3 + 6 adalah 9 bernilai benar.
- Pernyataan kedua yaitu 9 merupakan bilangan ganjil bernilai benar.
Kedua pernyataan bernilai benar, sehingga nilai kebenaran untuk konjungsi akan bernilai benar.
Selanjutnya, sekarang perhatikan contoh konjungsi yang bernilai salah. Bilangan prima terkecil adalah 1 dan 1 adalah bilangan ganjil.
- Pernyataan pertama yaitu Bilangan prima terkecil adalah 1 memiliki nilai kebenaran salah, karena bilangan prima terkecil adalah 2.
- Pernyataan kedua yaitu 1 adalah bilangan ganjil merupakan pernyataan benar.
Sesuai aturan pada operator konjungsi, nilai kebenaran dari pernyataan Bilangan prima terkecil adalah 1 dan 1 adalah bilangan ganjil adalah salah.
Baca Juga: Cara Melengkapi Tabel Kebenaran untuk Pernyataan Majemuk
2) Disjungsi (p ∨ q)
Berikutnya adalah pernyataan majemuk dengan kata penghubung atau yang disebut disjungsi. Simbol disjungsi dalam logika matematika adalah ∨. Selain kata atau, kata penghubung disjungsi yang biasa digunakan meliputi alias, kalau, apakah.
Nilai kebenaran dari disjungsi akan bernilai salah jika p dan q keduanya salah, selain itu nilainya benar. Tabel kebenaran disjungsi untuk dua preposisi diberikan seperti berikut.

Tabel kebenaran disjungsi untuk tiga pernyataan diberikan seperti berikut.

Contoh disjungsi dengan nilai kebenaran benar: Ir. H. Joko Widodo adalah presiden ke – 7 Indonesia atau Indonesia adalah nama sebuah kota.
- Pernyataan pertama yaitu Ir. H. Joko Widodo adalah presiden ke – 7 Indonesia bernilai benar.
- Pernyataan kedua yaitu Indonesia adalah nama sebuah kota bernilai salah, karena Indonesia adalah nama sebuah negara.
Jadi, disjungsi pernyataan majemuk Ir. H. Joko Widodo adalah presiden ke – 7 Indonesia atau Indonesia adalah nama sebuah kota bernilai benar.
Contoh disjungsi dengan nilai kebenaran salah: Indonesia merupakan negara dengan empat musim atau Indonesia terletak di benua Eropa.
- Nilai kebenaran dari pernyataan pertama adalah salah, karena Indonesia hanya memiliki dua musim.
- Nilai kebenaran dari pernyataan kedua juga salah, karena Indonesia terletak di benua Asia.
Sehingga, disjungsi pernyataan majemuk Indonesia merupakan negara dengan empat musim atau Indonesia terletak di benua Eropa adalah salah.
Baca Juga: Tautologi, Kontradiksi, dan Kontingensi
3) Implikasi (p → q)
Berikutnya adalah pernyataan majemuk dengan kata penghubung jika … maka …, yang disebut implikasi. Simbol dari implikasi berupa tanda panah (simbol: →). Selain jika … maka …, kata penghubung yang juga bisa digunakan pada implikasi adalah … mengakibatkan …, … jika…, … bilamana …, … hanya jika …, … syarat perlu bagi …, … syarat cukup bagi …, hanya dipisahkan tanda koma (…, …).
Nilai kebenaran dari implikasi hanya akan bernilai salah jika pernyataan pertama bernilai benar dan pernyataan kedua bernilai salah ( jika benar maka salah), selain itu bernilai benar.
Tabel kebenaran implikasi untuk dua pernyataan diberikan seperti berikut.

Tabel kebenaran implikasi untuk dua pernyataan diberikan seperti berikut.
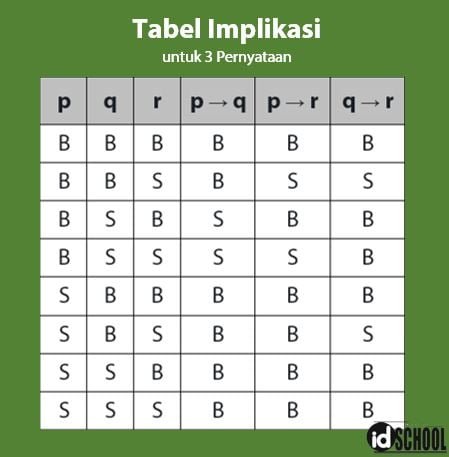
Contoh implikasi dengan nilai kebenaran benar: Jika bilangan prima terkecil adalah 1 maka 1 adalah bilangan ganjil.
- Pernyataan pertama bernilai salah karena bilangan prima terkecil adalah 2.
- Pernyataan kedua yaitu 1 adalah bilangan ganjil memiliki nilai kebenaran benar.
Nilai kebenaran dari implikasi pernyataan majemuk jika salah maka benar adalah benar. Sehingga, nilai kebenaran dari Jika bilangan prima terkecil adalah 1 maka 1 adalah bilangan ganjil adalah benar.
Contoh implikasi dengan nilai kebenaran salah: Jika hasil penjumlahan dua bilangan genap adalah bilangan genap maka hasil dari 2 + 4 sama dengan 5.
- Nilai kebenaran dari pernyataan pertama yaitu hasil penjumlahan dua bilangan genap adalah bilangan genap maka adalah benar.
- Nilai kebenaran dari pernyataan kedua yaitu hasil dari 2 + 4 sama dengan 5 adalah salah.
Nilai kebenaran untuk implikasi jika benar maka salah adalah salah. Sehingga, nilai kebenaran untuk jika hasil penjumlahan dua bilangan genap adalah bilangan genap maka hasil dari 2 + 4 sama dengan 5 adalah salah.
Baca Juga: Konvers, Invers, dan Kontraposisi dari Suatu Implikasi
4) Biimplikasi (p ↔ q)
Biimplikasi merupakan pernyataan majemuk dengan kata penghubungn … jika dan hanya jika … (simbol: ↔). Kata penghubung lain yang juga digunakan pada biimplikasi adalah bila dan hanya bila, syarat perlu dan cukup.
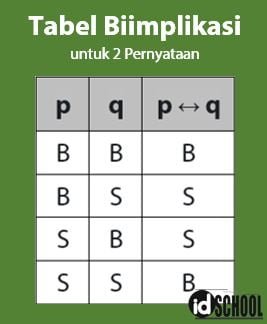
Nilai kebenaran dari suatu biimplikasi hanya akan bernilai benar apabila kedua pernyataan bernilai sama. Atau, suatu biimplikasi hanya akan bernilai benar jika kedua pernyataan bernilai benar atau keduanya bernilai salah.
Tabel kebenaran biimplikasi untuk dua pernyataan diberikan seperti berikut.
Tabel kebenaran biimplikasi untuk tiga pernyataan diberikan seperti berikut.

Contoh biimplikasi dengan nilai benar: Ayam adalah hewan berkaki empat jika dan hanya jika Kambing adalah hewan berkaki dua.
- Nilai kebenaran dari Ayam adalah hewan berkaki empat (pernyataan pertama) adalah salah.
- Nilai kebenaran dari Kambing adalah hewan berkaki dua (pernyataan kedua) adalah salah.
Sehingga, nilai kebenaran untuk biimplikasi pada contoh tersebut adalah benar.
Contoh biimplikasi dengan nilai salah: Kucing berkembang biak dengan bertelur jika dan hanya jika Ayam memiliki dua kaki.
- Nilai kebenaran dari pernyataan pertama adalah salah.
- Sedangkan nilai kebenaran dari pernyataan kedua adalah benar.
Nilai kebenaran dari salah jika dan hanya jika benar adalah salah. Jadi, nilai kebenaran untuk contoh tersebut adalah salah.
Baca Juga: Bentuk Ekuivalen Pernyataan Majemuk dalam Logika Matematika
Contoh Soal dan Pembahasan
Beberapa contoh soal logika matematika berikut dapat digunakan untuk melatih kemampuan sobat idschool. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Logika Matematika
Diketahui dua pertanyaan premis p = Dina rajin belajar dan q = Dina selalu mendapat nilai bagus. Konjungsi dari dua pernyataan tersebut adalah ….
A. Dina rajin belajar dan selalu mendapat nilai bagus
B. Dina rajin belajar atau selalu mendapat nilai bagus
C. Jika Dina rajin belajar maka Dina selalu mendapat nilai bagus
D. Dina rajin belajar jika dan hanya jika Dina selalu mendapat nilai bagus
E. Dina rajin belajar dan tidak mendapat nilai bagus
Pembahasan:
Konjungsi adalah pernyataan majemuk dengan kata penghubung dan. Sehingga, konjungsi dari dua pernyataan tersebut adalah Dina rajin belajar dan selalu mendapat nilai bagus.
Jawaban: A
Contoh 2 – Soal Logika Matematika
Simbol yang tepat untuk pernyataan Jika Ani rajin belajar maka Ani akan mendapatkan uang jajan lebih adalah ….
A. p ∨ q
B. p ∧ q
C. p → q
D. p ↔ q
E. p ~ q
Pembahasan:
Misalkan dua pernyataan pada soal disimbolkan dengan p dan q, sesuai pernyataan berikut.
- p = Ani rajin belajar
- q = Ani akan mendapatkan uang jajan lebih
Diberikan pernyataan Jika Ani rajin belajar maka Ani akan mendapatkan uang jajan lebih. Kata penghubung untuk menyatakan pernyataan jika … maka berupa tanda panah dengan satu anak panah (→).
Jadi, simbol yang tepat untuk pernyataan Jika Ani rajin belajar maka Ani akan mendapatkan uang jajan lebih adalah p → q.
Jawaban: C
Demikianlah ulasan materi logika matematika yang meliputi konjungsi, disjungsi, implikasi, dan biimplikasi. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Penarikan Kesimpulan dalam Logika Matematika
