Banyaknya pemetaan sama dengan banyak cara memasangkan domain (daerah asal) ke daerah kawa atau kodomain. Pemetaan sendiri merupakan relasi khusus pada dua himpunan yang memasangkan setiap anggota himpunan domain tepat satu ke himpunan kodomain. Pemetaan sering disebut juga sebagai fungsi.
Relasi adalah aturan yang memasangkan antara dua himpunan yaitu dari domain ke kodomain. Domain adalah himpunan yang memuat semua anggota yang akan dipasangkan, sementara kodomain adalah himpunan yang memuat semua anggota yang akan menjadi pasangan. Banyaknya pemetaan yang mungkin dari suatu himpunan ke himpunan lain tergantung dari banyaknya anggota dari kedua himpunan tersebut.
Diketahui A adalah himpunan dengan banyak anggota n(A) dan B adalah himpunan dengan banyak anggota n(B). Bagaiman cara menentukan banyaknya pemetaan dari himpunan A ke B? Bagaimana cara menentukan banyaknya pemetaan dari himpunan B ke A?
Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Relasi dan Pemetaan
- Banyaknya Pemetaan yang Mungkin
- Rumus Cara Menentukan Banyaknya Pemetaan yang Mungkin
- Contoh Soal Cara Menentukan Banyak Pemetaan dan Pembahasannya
Baca Juga: Himpunan dan Diagram Venn
Relasi dan Pemetaan
Sebelumnya, ingat kembali materi tentang apa itu relasi dan apa itu pemetaan atau fungsi. Di mana diketahui bahwa setiap pemetaan atau fungsi merupakan relasi, namun setiap relasi belum tentu merupakan fungsi/pemetaan.
Dalam pemetaan/fungsi, terdapat aturan khusus yang mengharuskan sebuah relasi memasangkan setiap anggota himpunan domain tepat satu pada anggota kodomain. Perhatikan relasi yang bukan merupakan pemetaan dan relasi yang merupakan pemetaan berikut.

Baca Juga: Domain, Kodomain, dan Range
Sudah ingat bagaimana sebuah relasi dikatakan sebagai pemetaan atau fungsi? Selanjutnya, sekarang bagaimana cara menentukan banyak pemetaan yang mungkin dari A ke B.
Banyaknya Pemetaan yang Mungkin
Diberikan dua buah himpunan A dan B. Diketahui bahwa anggota himpunan A sama dengan n anggota. Sedangkan banyaknya anggota himpunan B sama dengan m anggota. Berapa banyaknya pemetaan yang mungkin dari A ke B? Berapa banyak cara menentukan pemetaan yang mungkin dari B ke A. Apakah pemetaan yang mungkin dari A ke B sama dengan pemetaan dari B ke A?
Untuk mengetahui jawabannya perhatikan sebuah contoh sederhana berikut.
Diberikan dua buah himpunan yaitu himpunan A dan himpunan B. Misalkan anggota himpunan A = {a, b} dan himpunan B = {1, 2, 3}. Himpunan A memiliki anggota himpunan sebanyak 2 anggota dan anggota B memiliki anggota sebanyak 3 anggota. Pemetaan dari A ke B dan pemetaan dari B ke A sesuai dengan penjelasan berikut.
1) Pemetaan dari A ke B
Diketahui: A = {a, b} dan B = {1, 2, 3}
Banyaknya pemetaan yang mungkin dari A ke B diberikan seperti diagram-diagram fungsi berikut.
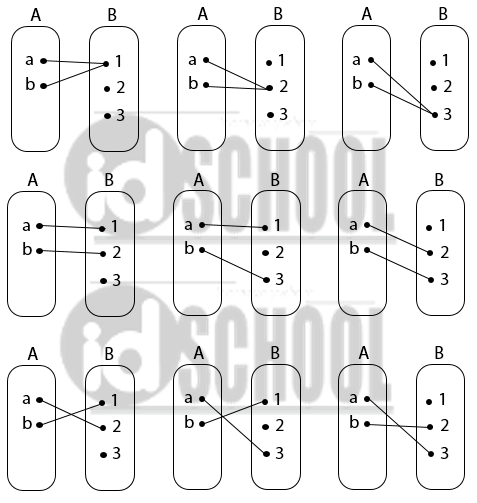
Dari gambar pemetaan yang mungkin dapat diketahui bahwa banyaknya pemetaan yang mungkin dari A ke B ada 9 cara.
2) Pemetaan dari B ke A:
Diketahui: B = {1, 2, 3} dan A = {a, b}
Banyaknya pemetaan yang mungkin dari B ke A diberikan seperti diagram-diagram fungsi berikut.

Dari gambar pemetaan yang mungkin dapat diketahui bahwa banyaknya pemetaan yang mungkin dari B ke A ada 8 cara.
Apa Kesimpulannya?
Apakah banyaknya pemetaan dari A ke B sama dengan banyaknya pemetaan dari B ke A? Jawabannya adalah TIDAK!
Hasil bahasan di atas menunjukkan bahwa hasilnya tidak sama. Namun, hasilnya bisa jadi sama jika banyaknya anggota himpunan A sama dengan anggota himpunan B. Karena banyaknya pemetaan yang mungkin tergantung pada banyaknya anggota pada kedua himpunan.
Kesimpulan: banyaknya pemetaan dari A ke B tidak sama dengan pemetaan dari B ke A (untuk banyak anggota himpunan A dan himpunan B yang berbeda)
idschool(dot)net
Baca Juga: Contoh-Contoh Kalimat Terbuka dan Tertutup dalam Matematika
Rumus Cara Menentukan Banyaknya Pemetaan yang Mungkin
Mencari banyaknya pemetaan yang mungkin dengan cara menggambar semua kemungkinan seperti cara yang dilakukan pada bahasan di atas tentu tidak dianjurkan. Kebetulan, banyaknya anggota yang dijadikan contoh seperti di atas masih memungkinkan untuk menentukan pemetaan yang mungkin dengan mendaftar.
Namun, untuk banyak anggota yang lebih banyak tentu akan menjadi sebuah kendala tersendiri. Tentu saja akan selalu ada solusi untuk sebuah permasalahan.
Banyaknya pemetaan yang mungkin dari A ke B atau pemetaan yang mungkin dari B ke A dapat diketahui melalui sebuah rumus cepat. Rumus yang dapat digunakan untuk menentukan banyaknya pemetaan yang mungkin adalah n(B)n(A) dan n(A)n(B) sesuai dengan ketentuan berikut.
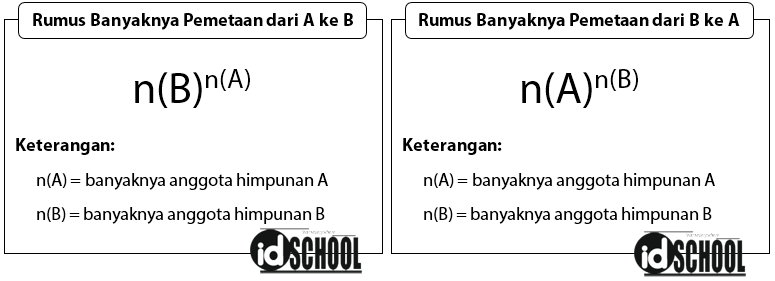
Perhatikan kembali pada contoh soal yang diberikan sebelumnya, yaitu diberikan himpunan A dan himpunan B.
Diketahui:
A = {a, b} → n(A) = 2
B = {1, 2, 3} → n(B) = 3
Banyaknya pemetaan:
Dari A ke B = n(B)n(A) = 32 = 9
Dari B ke A = n(A)n(B) = 23 = 8
Dengan menggunakan rumus yang diberikan di atas dapat diperoleh hasil yang sama seperti pada cara menentukan banyaknya cara pemetaan yang mungkin dengan mendaftar semua diagram, bukan?
Baca Juga: Cara Menentukan Banyaknya Anggota Himpunan Bagian
Contoh Soal Cara Menentukan Banyak Pemetaan dan Pembahasannya
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Mencari Banyaknya Cara Pemetaan yang Mungkin

Diketahui P = {2, 4, 6, 8} dan Q = {a, b, c}. Banyaknya pemetaan yang mungkin dari P ke Q adalah ….
A. 81
B. 64
C. 27
D. 12
Pembahasan:
Dari soal dapat diketahui banyak anggota P atau n(P) dan anggota Q atau n(Q) seperti berikut.
P = {1, 4, 6, 8} → n(P) = 4
Q = {a, b, c} → n(Q) = 3
Banyaknya pemetaan dari P ke Q = n(Q)n(P)
= 34
= 3 × 3 × 3 × 3 = 81
Jadi, banyaknya pemetaan yang mungkin dari P ke Q adalah 81 cara.
Jawaban: A
Contoh 2 – Mengenali Relasi yang Merupakan Pemetaan
Diketahui P = {1, 2, 3, 4} dan Q = {k, l, m, n, o}
Himpunan pasangan berurutan dari himpunan P ke himpunan Q yang merupakan pemetaan adalah ….
A. {(1, k); (2, l); (3, m)}
B. {(1, l); (2, k); (3, n); (4, m)}
C. {(1, k); (1, l); (1, m); (1, n); (1, o)}
D. {(1, k); (2, l); (3, m); (4, n); (4, o)}
Pembahasan:
Pemetaan dapat dikenali dari anggota domain yang tepat satu terpasangkan dengan anggota kodomian. Atau dapat juga dikatakan bahwa semua anggota domain memiliki pasangan dan hanya satu kali dipasangkan. Pada himpunan pasangan berurutan, pemetaan dapat dikenali dari absis (nilai yang didepan) hanya muncul sekali dan semua himpunan muncul.
Untuk himpunan P = {1, 2, 3, 4} semuanya terpasangkan tepat satu kali terdapat pada pilihan B. Pada pilihan A ada 1 anggota (yaitu 4) yang tidak terpasangkan, pilihan C memasangkan satu anggota (yaitu 1) sebanyak lima kali. Sementara piilihan D memesangkan anggota 4 sebanyak dua kali.
Jadi, himpunan pasangan berurutan dari himpunan P ke himpunan Q yang merupakan pemetaan adalah {(1, l); (2, k); (3, n); (4, m)}.
Jawaban: D
Contoh 3 – Banyak Pemetaan
Jika M = {faktor dari 6} dan N = {a, b, c} maka banyak pemetaan atau fungsi dari N ke M adalah ….
A. 16
B. 27
C. 64
D. 81
Pembahasan:
Langkah pertama adalah menentukan banyak anggota dari himpunan M dan himpunan M seperti yang dilakukan pada berikut.
Banyak anggota M dan N:
M = {faktor dari 6} = {1, 2, 3, 6} → n(M) = 4
N = {a, b, c} → n(N) = 3
Menghitung banyak pemetaan dari N ke M
= n(M)n(N)
= 43 = 4×4×4 = 64 cara
Jadi, banyak pemetaan atau fungsi dari N ke M adala 64 cara.
Jawaban: C
Demikianlah ulasan materi mengenai cara menentukan banyak pemetaan yang meliputi ulasan apa itu pemetaan, banyaknya, dan rumus menentukan banyaknya pemetaan beserta caranya Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Kumpulan Soal UN SMP – Relasi dan Fungsi
Sangat membantu , jadi di bookmark nih artikel