Suatu implikasi memiliki bentuk konvers invers dan kontraposisi yang dapat dinyatakan melalui suatu hubungan. Konvers adalah logika yang merupakan kebalikan dari imlplikasi, sementara invers adalah logika negasi dari implikasi. Sedangkan kontraposisi adalah logika yang merupakan kebalikan dan negasi dari suatu implikasi. Implikasi tidak ekuivalen dengan konvers dan invers, namun implikasi ekuivalen dengan kontraposisi dan konvers ekuivalen dengan invers.
Misalkan terdapat suatu bentuk implikasi p → q maka bentuk konvers invers dan kontraposisi dari implikasi tersebut berturut-turut adalah q → p, ~p → ~q, dan ~q → ~p. Hubungan antara implikasi dengan konvers invers dan kontraposisi diringkas seperti diagram berikut.
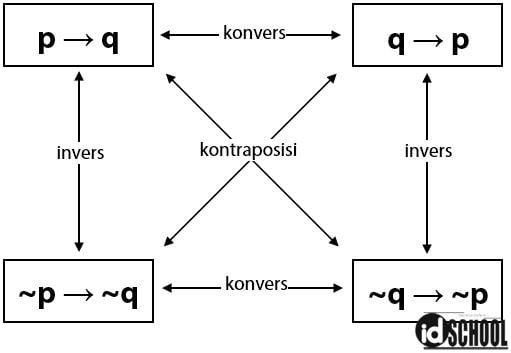
Baca Juga: 3 Metode Penarikan Kesimpulan
Bagaimana perbandingan nilai kebenaran implikasi dengan bentuk konvers invers dan kontraposisi dari implikasi tersebut? Apa saja perbedaan konvers invers dan kontraposisi dari suatu implikasi? Sobat idschool dapat mencari tahu jawabannya seputar konvers invers dan kontraposisi dari suatu implikasi melalui ulasan di bawah.
Table of Contents
Implikasi
Operator logika matematika untuk implikasi diberikan dalam bentuk garis lurus dengan sebuah anak panah pada ujung kanan (simbol implikasi: →). Dalam implikasi terdapat anteseden dan konsekuen, di mana anteseden merupakan penyabab dan konsukuen merupakan akibat. Untuk implikasi p → q maka yang disebut anteseden adalah p dan konsekuen adalah q.
Suatu implikasi memiliki nilai kebenaran Salah (S) atau False (F) untuk anteseden bernilai benar dan konsekuen bernilai salah (B → S). Selain itu nilai kebenaran dari suatu implikasi adalah Benar (B) atau True (T) seperti yang ditunjukkan pada tabel berikut.
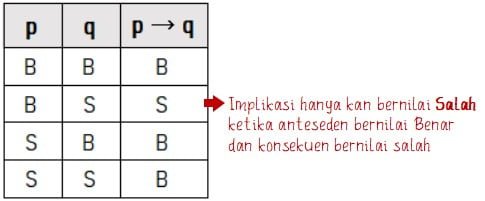
Dalam sebuah implikasi juga terdapat syarat cukup dan syarat perlu. Untuk implikasi jika p maka q, p adalah syarat cukup bagi q sedangkan q adalah syarat perlu bagi p.
Misalkan diketahui dua buah proposisi tunggal p dan q, bentuk implikasi dari dua proposisi tersebut adalah jika p maka q yang disimbolkan dengan p → q. Sebagai contoh dua proposisi yaitu Ani kehujanan dan Baju Ani menjadi basah. Implikasi dari dua proposisi tersebut adalah Jika Ani kehujanan maka baju Ani menjadi basah.
Pada contoh implikasi yang diberikan, Kehujanan merupakan syarat cukup untuk baju Ani menjadi basah. Sedangkan baju Ani menjadi basah merupakan syarat perlu bagi Ani kehujanan.
Alasannya, penyebab baju Ani menjadi basah bisa dikarenakan banyak hal seperti tersiram air, jatuh ke selokan, berkeringat, dan lain sebagainya. Sehingga kehujanan menjadi syarat cukup bagi baju Ani menjadi basah. Sementara baju basah menjadi syarat perlu untuk Ani kehujanan.
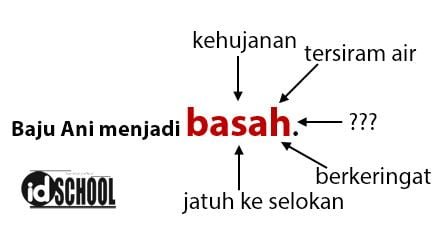
Baca Juga: Tautologi, Kontradiksi, dan Kontingensi
Bentuk Konvers Invers dan Kontraposisi dari Suatu Implikasi p → q
Konvers invers dan kontraposisi menggunakan simbol yang sama dengan implikasi yaitu →. Sebelumnya sudah disebutkan bahwa konvers ekuivalen dengan invers sementara implikasi ekuivalen dengan kontraposisi. Bentuk ekuivalen dari suatu proposisi majemuk dapat diketahui melalui nilai kebenaran yang sama.
Nilai kebenaran pada konvers invers dan kontraposisi diberikan seperti masing-masing ulasan berikut.
1) Konvers: q → p
Konvers pada bahasan logika matematika merupakan kondisi dimana anteseden dan konsekuen dari suatu implikasi bertukar posisi/tempat. Sebagai contoh: diberikan sebuah implikasi p → q maka konvers dari implikasi tersebut adalah q → p. Bentuk implikasi dan konvers tidak ekuivalen karena tabel kebenaran tidak menunjukkan nilai kebenaran yang sama.
Nilai kebenaran dari suatu implikasi dan konvers sesuai dengan nilai-nilai pada tabel kebenaran berikut.
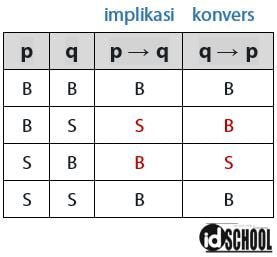
Berdasarkan tabel kebenaran di atas terlihat bahwa nilai kebenaran implikasi dan konvers berbeda. Perbedaan pertama terdapat pada saat anteseden bernilai benar (B) dan konsekuen bernilai salah (S). Perbedaan kedua terdapat pada saat anteseden bernilai salah (S) dan konsekuen bernilai salah (B).
Contoh implikasi dari konvers dari suatu implikasi:
- Implikasi: Jika ibu guru tidak memberikan pekerjaan rumah maka murid – murid menjadi senang.
Konvers: Jika murid – murid menjadi senang maka ibu guru tidak memberikan pekerjaan rumah.
- Implikasi: Jika Anton bagun kesiangan maka Anton terlambat ke sekolah.
Konvers: Jika Anton terlambat ke sekolah maka Anton bagun kesiangan.
Kesimpulan yang dapat diambil adalah implikasi tidak ekuivalen dengan konvers. Sehingga proposisi untuk bentuk implikasi tidak bernilai sama dengan bentuk konversnya.
2) Invers: ~p → ~q
Fungsi invers dalam matematika secara umum merupakan kebalikan aksi dari suatu fungsi. Pada logika matematika, invers dari suatu implikasi sama dengan bentuk implikasi dari ingkaran anteseden dan ingkaran konsekuen.
Diketahui sebuah implikasi p → q maka bentuk invers dari implikasi tersebut adalah ~p → ~q (jika bukan p maka bukan q). Kedua bentuk implikasi ini memiliki nilai yang berbeda (tidak saling ekuivalen). Untuk melihat perbedaan implikasi dan invers terdapat pada tabel kebenaran berikut.
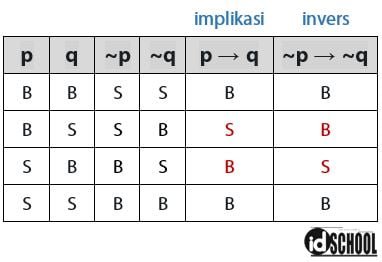
Berdasarkan tabel kebenaran di atas, implikasi dan invers memiliki nilai kebenaran yang berbeda. Perbedaan pertama terdapat pada saat anteseden bernilai benar (B) dan konsekuen bernilai salah (S). Perbedaan kedua terdapat pada saat anteseden bernilai salah (S) dan konsekuen bernilai salah (B).
Contoh implikasi dan invers dari suatu implikasi:
- Implikasi: Jika ibu guru tidak memberikan pekerjaan rumah maka murid – murid menjadi senang.
Invers: Jika ibu guru memberikan pekerjaan rumah maka murid – murid tidak menjadi senang.
- Implikasi: Jika Anton bagun kesiangan maka Anton terlambat ke sekolah.
Invers: Jika Anton tidak bagun kesiangan maka Anton tidak terlambat ke sekolah.
Implikasi tidak ekuivalen dengan inversnya, sehingga proposisi-proposisi antara implikasi tidak sama dengan invers.
3) Kontraposisi: ~q → ~p
Bentuk kontraposisi dari suatu implikasi merupakan pembalikan bentuk inversnya. Kondisi ini sama dengan bentuk implikasi dari ingkaran konsekuen dan ingkaran antesedennya.
Jika diketahui sebuah implikasi p → q maka kontraposisi dari implikasi tersebut adalah ~q → ~p (jika bukan q maka bukan p). Kedua bentuk implikasi ini merupakan bentuk ekuivalen yang dapat ditunjukkan melalui semua nilai kebenaran yang sama seperti pada tabel kebenaran berikut.
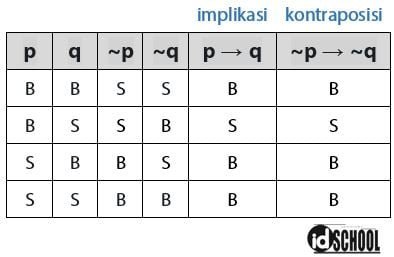
Contoh implikasi dan kontraposisi dari implikasi tersebut:
- Implikasi: Jika ibu guru tidak memberikan pekerjaan rumah maka murid – murid menjadi senang.
Kontraposisi: Jika murid – murid tidak menjadi senang maka ibu guru memberikan pekerjaan rumah
- Implikasi: Jika Anton bagun kesiangan maka Anton terlambat ke sekolah.
Kontraposisi: Jika Anton tidak terlambat ke sekolah maka Anton tidak bagun kesiangan.
Nilai kebenaran pada kolom implikasi sama dengan nilai kebenaran pada bentuk kontraposisinya sehingga dua bentuk implikasi tersebut ekuivalen. Sehingga proposisi-proposisi antara implikasi dan kontraposisi merupakan pernyataan yang ekuivalen.
Sekian ulasan materi bentuk konvers invers dan kontraposisi dari suatu implikasi beserta hubungan ketiganya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Logika Matematika (Konjungsi, Disjungsi, Implikasi, Biimplikasi)
