Fungsi trignomteri memiliki bentuk kurva berupa fungsi periodik yang nilainya berulang mebentuk suatu pola. Grafik fungsi trigonometri mempunyai amplitudo yang besar nilainya sama dengan harga mutlak nilai minimum dan maksimum fungsi trigonometri. Dalam grafik fungsi trigonometri juga terdapat periode yang menyatakan berapa memuat satu gelombang untuk setiap periode .
Fungsi dasar trigonometri meliputi fungsi sinus, cosinus, dan tangen. Selain ketiga fungsi dasar tersebut terdapat juga fungsi cosec (1/sin), sec (1/cos), cotan (1/tan), dan bentuk kombinasi fugsi dasar trigonometri lainnya.
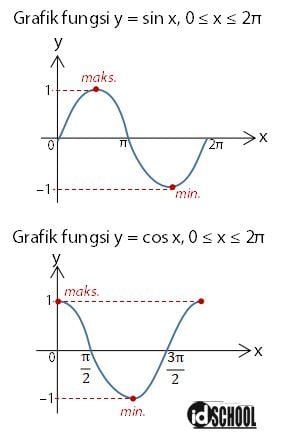
Besar nilai minimum dan maksimum fungsi trigonometri untuk fungsi dasar y = sin x dan y = cos x berturut-turut adalah –1 dan 1. Nilai minimum y = sin x salah satunya terjadi saat nilai x = 3/2π dan nilai minimum y = cos x dicapai saat (salah satunya) x = π. Sedangkan nilai maksimum y = sin x dicapai saat (salah satunya) x = 1/2π dan nilai maksimum y = cos x dicapai saat (salah satunya) x = 0.
Hasil tersebut dapat secara mudah diperoleh dengan melihat grafik fungsi y = sin x dan y = cos x.
Bentuk fungsi trignometri dapat berupa fungsi yang lebih rumit, misalnya y = sin 3x + cos 3x, y = 2 cos 2x – 4 sin x, atau bentuk yang lebih rumit lainnya. Fungsi trigonometri yang lebih rumit membutuhkan cara lain untuk menentukan nilai minimum dan maksimumnya.
Bagaimana cara menentukan nilai minimum dan maksimum fungsi trigonometri dengan berbagai bentuk? Sobat idschool dapat mencari cara mendapatkannya melalui ulasan di bawah.
Table of Contents
- 3 Cara Menentukan Nilai Minimum dan Maksimum Fungsi Trigonomteri
- Contoh Soal dan Pembahasan Nilai Minimum dan Maksimum Fungsi Trigonometri
Baca Juga: Cara Menggambar Grafik Fungsi y = sin x, y = 2 sin x, dan y = sin 2x
3 Cara Menentukan Nilai Minimum dan Maksimum Fungsi Trigonomteri
Ada tiga cara yang dapat digunakan untuk menentukan nilai minimum dan maksimum fungsi trigonometri. Mana yang paling bagus untuk digunakan? Jawabannya adalah bergantung dari bentuk persamaan tirgonometri yang akan dicari nilai minimum/maksimum.
Ketiga cara untuk menentukan nilai minimum dan maksimum fungsi trigonometri terdapat pada masing-masing bahasan di bawah.
1. Fungsi Trigonometri y = A sin x + C atau y = A cos x + C
Bentuk fungsi yang pertama ini dapat dikatakan cukup sederhana. Sehingga cara untuk menentukan nilai minimum dan maksimumnya juga cukup mudah dilakukan.
Nilai maksimum dan minimum fungsi trigonometri untuk fungsi sinus dan cosinus dapat ditentukan melalui amplitudo (A) dan konstanta (k). Amplitudo adalah simpangan terjauh sedangkan konstanta merupakan faktor bergesernya kurva secara vertikal.
Fungsi dasar y = sin x dan y = cos x memiliki nilai minimum = –1 dan nilai maksimum = 1. Dua keterangan ini akan sangat membantu dalam menentukan nilai minimum dan maksimum fungsi trigonometri yang serupa, misalnya y = k sin x + C atau y = k cos x + C.
Persamaan umum untuk menentukan nilai minimum dan maksimum fungsi trigonometri dengan bentuk tersebut diberikan seperti berikut.

Bentuk fungsi trigonometri ini cukup mudah untuk ditentukan nilai minimum dan maksimumnya. Perhatikan cara menentukan nilai minimum dan maksimum pada fungsi-fungsi trigonometri berikut.
- f(x) = –sin x
Nilai maksimum = |–1| = 1
Nilai minimum = – |–1| = –1
- g(x) = 3 cos (x – 15°)
Nilai maksimum = | 3 | = 3
Nilai minimum = – | 3 | = –3
- p(x) = –4 cos x + 1
nilai maksimum = |– 4| + 1 = 4 + 1 = 5
nilai minimum = –| –4 | + 1 = –4 + 1 = –3
2. Fungsi Trigonometri Y = A sin x + B cos x + C
Bentuk fungsi trigonometri dapat dinyatakan dalam kombinasi fungsi y = A sin x + B cos x + C. Cara menentukan nilai minimum dan maksimum pada bentuk fungsi trigonometri tersebut dilakukan dengan cara lain. Di mana nilai minimum dan maksimum fungsi trigonometri tersebut dapat dicari dengan melakukan perubahan ke dalam persmaan bentuk lain terlebih dahulu.
Rumus atau persamaan umum yang dapat digunakan untuk melakukan transformasi persamaan sesuai dengan bentuk berikut.
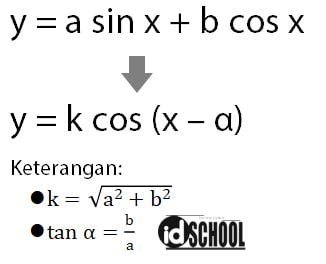
Bagaimana penggunaan persamaan di atas untuk menentukan nilai minimum dan maksimum fungsi trigonometri dapat dilihat seperti berikut.
Soal 1:
Tentukan nilai minimum dan maksimum fungsi f(x) = 3 cos x + 4 sin x + 1!
Mencari nilai k:
k = √(32 + 42)
k = √25 = 5
Sehingga, f(x) = 3 cos x + 4 sin x + 1 = 5 cos (x – α) + 1 dengan nilai minimum cos (x – α) = –1 dan nilai maksimum cos (x – α) = 1
- Nilai minimal f(x) = 5 cos (x – α) + 1 = 5(–1) + 1 = –5 + 1 = –4
- Nilai maksimal f(x) = 5 cos (x – α) + 1 = 5 + 1 = 6
Soal 2:
Tentukan nilai minimum dan maksimum dari f(x) = 2 cos x + √5 sin x – 1!
- Mencari nilai k:
k = √(22 + √52) - k = √(4 + 5) = √9 = 3
- Diketahui f(x) = 2 cos x + √5 sin x – 1
Persamaan tersebut dapat dinyatakan dalam persamaan f(x) = 3 cos (x – α) – 1.
- f(x) = 2 cos x + √5 sin x – 1 → f(x) = 3 cos (x – α) – 1
Diketahui bahwa nilai minimum cos (x – α) = – 1 dan nilai maksimum cos (x – α) = 1, sehingga nilai minimum dan maksimum fungsi trigonometeri tersebut adalah,
Nilai minimal f(x) = 3 cos(x–α) – 1 = 3(–1) + 1 = –2
Nilai maksimal f(x) = 3 cos(x–α) – 1 = 3(1) + 1 = 4
Baca Juga: Menyelesaikan Persamaan Fungsi Trigonometri
3. Nilai Minimum dan Maksimum Fungsi Trigonometri dengan Turunan
Cara berikutnya adalah menentukan nilai minimum dan maksimum fungsi trigonometri dengan turunan. Diketahui bahwa titik statsioner suatu fungsi terjadi saat turunan pertama fungsi sama dengan nol. Aturan ini juga berlaku untuk fungsi trigonometeri.
Turunan pertama dari fungsi trigonometri sama dengan nol akan menghasilkan letak absis untuk titik puncak kurva. Titik puncak tersebut dapat berupa nilai minimum atau nilai maksimum. Substitusi nilai absis yang diketahui pada persamaan akan menghasilkan nilai minimum atau nilai maksimum fungsi tersebut.
Sebagai contoh akan ditentukan nilai minimum dan maksimum fungsi trigonometri f(x) = 3 cos x + 4 sin x + 1.
Menentukan persamaan: f’(x) = 0
–3 sin x + 4 cos x = 0
–3 sin x = –4 cos x
sin x/cos x = –4/–3 = 4/3
tan x = 4/3
Proses perhitungan di atas menunjukan hasil bahwa nilai tan x = 3/4, sehingga dapat diperoleh dua kondisi. Dua kondisi tersebut berlaku untuk nilai minimum dan nilai maksimum.

Sehingga, nilai minimum dan maksimum untuk fungsi f(x) = 3 cos x + 4 sin x + 1 adalah sebagai berikut.
- Nilai minimum f(x) = 3 cos x + 4 sin x + 1
= 3(–3/5) + 4(–4/5) + 1
= –9/5 – 16/5 + 1 = –4
- Nilai maksimum f(x) = 3 cos x + 4 sin x + 1
= 3(3/5) + 4(4/5) + 1
= 9/5 + 16/5 + 1 = 6
Diperoleh hasil yang sama dengan sebelumnya, bukan?
Baca Juga: Cara Menggambar Grafik Fungsi Trigonmetri y = cos x, y = 2 cos x, y = cos 2x
Cara menentukan nilai minimum dan maksimum fungsi trigonometri dapat dilakukan untuk semua bentuk fungsi trigonometri. Namun, cara ini membutuhkan waktu sedikit lebih lama dilakukan dari dua cara sebelumnya. Sehingga, cara ini baik digunakan untuk fungsi trigonometri yang kompleks atau sangat rumit .
Contoh Soal dan Pembahasan Nilai Minimum dan Maksimum Fungsi Trigonometri
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman sobat idschool. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal Nilai Minimum Fungsi Trigonometri
Nilai terkecil yang dapat dicapai oleh y = 3 – 2 · sin x · cos x adalah ….
A. 3
B. 2
C. 1
D. 0
E. –2
Pembahasan:
Mencari bentuk lain dari persamaan fungsi trigonometri y = 3 – 2 sinx cos x:
y = 3 – 2 sinx cos x
y = 3 – sin 2x
Grafik sin x memiliki nilai tertinggi atau maksimum 1, sehingga nilai maksimum yang dapat dicapai sin 2x adalah 1. Jadi, nilai nilai terkecil yang dapat dicapai oleh y adalah,
y = 3 – 2 sin x cos x
y = 3 – sin 2x
y = 3 – 1 = 2.
Jadi, nilai terkecil yang dapat dicapai oleh y = 3 – 2 sinx cos x adalah 2.
Jawaban: B
Contoh 2 – Soal Nilai Maksimum Fungsi Trigonometri
Diketahui x = cos A – 2 sin B dan y = sin A + 2 cos B. Nilai minimum dari x2 + y2 = ….
A. 1
B. 2
C. 3
D. 4
E. 5
Pembahasan:
Berdasarkan soal dapat diketahui persamaan-persamaan berikut.
- x = cos A – 2 sin B
→ x2 = cos2A – 4 cos A sin A + 4 sin2B
- y = sin A + 2 cos B
→ y2 = sin2A + 4 sin A cos B + 4 cos2B
Menentukan persamaan x2 + y2:
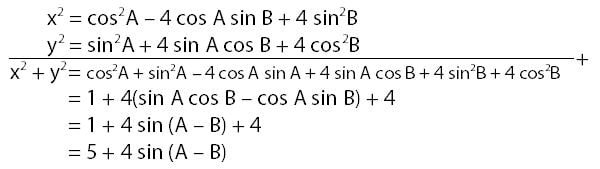
Nilai minimim untuk sin (A – B) adalah –1, sehingga nilai minimum untuk x2 + y2 adalah, x2 + y2 = 5 + 4 sin (A – B)
= 5 + 4(–1) = 1.
Jawaban: A
Contoh 3 – Soal Nilai Minimum dan Maksimum Fungsi Trigonometri

Pembahasan:
Informasi yang diberikan pada soal memuat beberapa persamaan berikut.
- x = sin α + √3 sin β
x2 = sin2α + 2√3 sin β sin α + 3 sin2β
- y = cos α + √3 cos β (cos α + √3 cos β)
y2 = cos2α + 2√3 cos α cos β + 3 cos2β
Persamaan untuk x2 + y2:
x2 + y2 = sin2α + 2√3 sin β sin α + 3 sin2β + cos2α + 2√3 cos α cos β + 3 cos2β
x2 + y2 = sin2α + cos2α + 2√3 sin β sin α + 2√3 cos α cos β + 3 sin2β + 3 cos2β
x2 + y2 = 1 + 2√3 (cos α cos β + sin α sin β) + 3 · 1
x2 + y2 = 4 + 2√3 cos (α – β)
Diperoleh persamaan x2 + y2 = 4 + 2√3 sin (α + β) yang nilainya akan maksimum saat nilai sin (α + β) maksimum. Nilai sin (α + β) maksimum sama dengan 1, sehingga nilai x2 + y2 akan maksimum saat memenuhi persamaan berikut.
x2 + y2 = 4 + 2√3 sin (α + β)
x2 + y2 = 4 + 2√3 · 1 = 4 + 2√3
Jadi, nilai a = 4, b = 2, dan a + b = 4 + 2 = 6
Jawaban: C
Demikianlah tadi ulasan cara menghitung nilai minimum dan maksimum fungsi trigonometri. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Limit pada Fungsi Trigonometri
