Cara menggambar grafik fungsi trigonometri y=cos x dapat dilakukan secara manual menggunakan pensil dan kertas melalui beberapa langkah. Bentuk grafik fungsi trigonometri y=cos x seperti dua buah parabola dengan arah terbukan berlawanan bukaan yang saling terhubung. Grafik fungsi trigonometri y=cos x selanjutnya dapat digunakan untuk membentuk grafik fungsi cosinus lain seperti y = 2 cos x, y = 2 cos x, y = cos 2x. y = cos (x+30o), dan lain sebagainya.
Grafik fungsi trigonometri y=cos x dapat digambar pada bidang datar dengan sumbu x berisi daftar sudut dan sumbu y meupakan nilainya. Nilai tertinggi pada fungsi y = cos x adalah 1 dan nilai terendahnya sama dengan -1. Sudut-sudut pada sumbu x merupakan sudut-sudut istimewa di mana nilai dari fungsi y=cos x berupa suatu nilai yang banyak diketahui. Bentuk bidang datar untuk menggambarkan grafik fungsi trigonometri y=cos x ditunjukkan seperti berikut.
Baca Juga: Fungsi Trigonometri dan Sudut Istimewa pada Trigonometri
Bagaimana cara menggambar grafik fungsi trigonometri y = cos x? Bagaimana cara menggambar grafik fungsi trigonometri y= 2 cos x, y = cos 2x, y = cos x + 1, atau fungsi cosinus lainnya? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Cara Menggambar Grafik Fungsi Trigonometri y=cos x
Sebelum mulai menggambar grafiknya, persiapkan peralatannya terlebih dahulu. Peralatan yang digunakan untuk menggambar grafik fungsi sinus trigonometri y = cos x adalah kertas, busur, jangka, dan pensil. Oke, mari kita mulai menggambar grafik fungsi trigonometri y = cos x.
Langkah-langkah menggambar grafik fungsi trigonometri y=cos x:
- Buat diagram kartesius, sumbu x mewakili sudutnya (dalam satuan derajat) dan sumbu y mewakili nilai fungsi nya.
- Buat lingkaran menggunakan jangka di sebelah kiri sumbu y.
- Ukur sudut istimewa pada lingkaran menggunakan busur. Tentukan semua letak titik koordinat yang mewakili sudut istimewa dan nilai fungsi trigonometrinya. Sudut istimewa dalam fungsi trigonometri yang biasa digunakan antara lain meliputi 30o, 45o, 60o, 90o, 120o, 135o, 150o, 180o, 210o, 225o, 240o, 270o, 300o, 330o, dan 360o.
- Hubungkan titik-titik yang diperoleh.
Contoh cara menggambar grafik fungsi trigonometri y = cos x dapat dilihat melalui beberapa langkah berikut.
Langkah #1:
Buat diagram kartesius, sumbu x mewakili sudutnya (dalam satuan derajat) dan sumbu y mewakili nilai fungsi nya.

Langkah #2:
Buat lingkaran di sebelah kiri sumbu y.
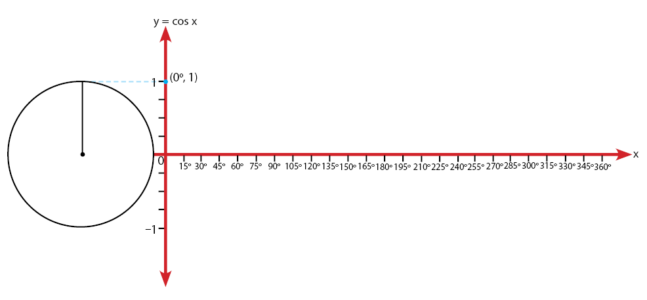
Langkah #3:
Ukur sudut istimewa pada lingkaran menggunakan busur. Tentukan semua letak titik koordinat yang mewakili sudut istimewa dan nilai fungsi trigonometrinya. Letak beberapa koordinat untuk besar sudut (α = 0o, 30o, 45o , 60o , 90o ) dan nilanya ditunjukkan pada gambar-gambar berikut
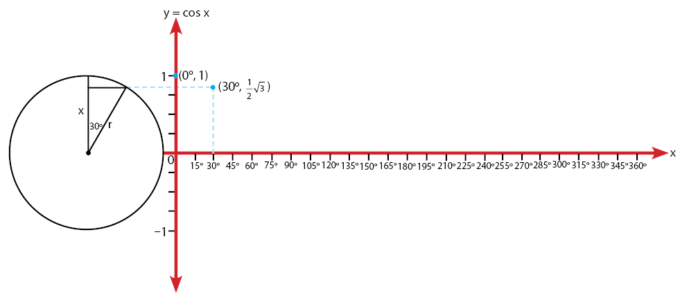
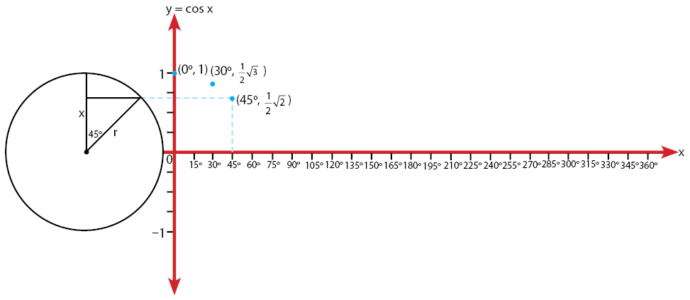
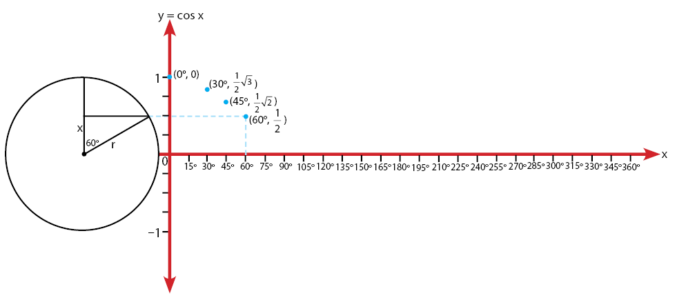



Serta, lakukan untuk semua sudut istimewa sehingga diperoleh semua pasangan antara sudut istimewa antara 0o– 360o dengan nilainya.
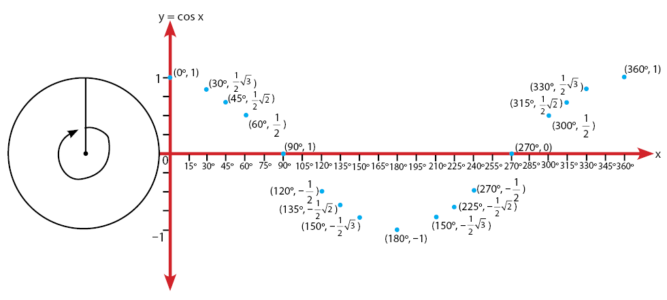
Langkah #4:
Hubungkan titik-titik yang diperoleh, sehingga terbentuk grafik fungsi y = cos x seperti gambar di bawah.

Baca Juga: Cara Menggambar Grafik Fungsi Trigonometri y = sin x, y = 2 sin x, dan y = sin 2x
Persamaan Umum Grafik Fungsi Cosinus Trigonometri
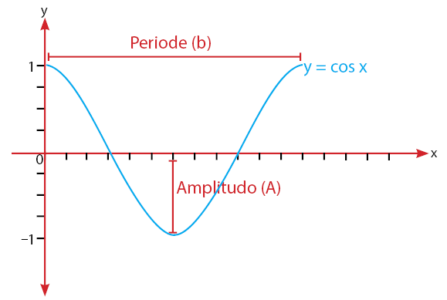
Secara umum, persamaan grafik fungsi cosinus trigonometri dapat dinyatakan melalui rumus seperti berikut.
y = A cos b(x ± α) ± c
Keterangan:
A = simpangan terjauh/amplitudo
b = banyaknya gelombang dalam rentang 0 – 2π
α = grafik geser ke kiri (+) atau ke kanan (–)
c = grafik geser ke atas (+) atau ke bawah (–)
Grafik dasar dari fungsi trigonometri y=cos x dan persamaan umum fungsi trigonometri di atas dapat digunakan untuk mempermudah pembuatan grafik fungsi cosinus lain. Beberapa fungsi cosinus antara lain y = 2 cos x, y = cos 2x, y = cos (x + 30o), y = cos x + 1, dan lain sebagainya. Selanjutnya, perhatikan beberapa grafik yang diperoleh dari pengembangan grafik fungsi trigonometri y=cos x dan grafik beberapa fungsi cosinus lain seperti beirkut..
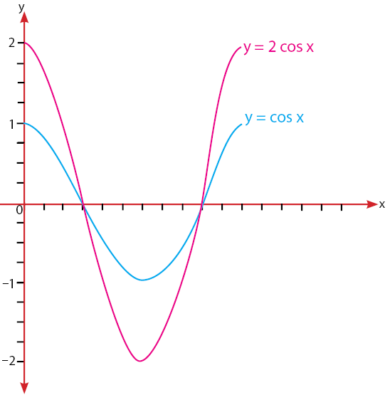
Grafik y = cos x dan y = 2 cos x: nilai amplitudonya berubah dari 1 menjadi 2.
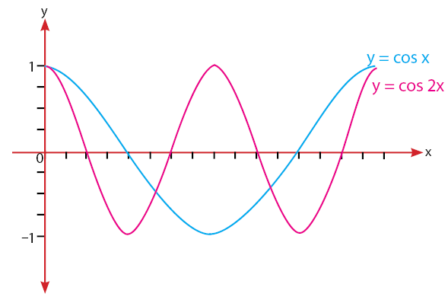
Grafik y = cos x dan y = cos 2x: banyaknya gelombang dalam rentang satu periode dari satu gelombang menjadi dua gelombang.
Grafik y = cos x dan y = cos (x – 30): geser grafik y = cos x ke arah kanan sejauh 30o.

Grafik y = cos x dan y = cos x + 1: Geser grafik y = cos x ke arah atas sebanyak satu satuan.

Sekian pembahasan mengenai cara menggambar grafik fungsi trigonometri y=cos x, y = 2 cos x, dan y = cos 2x. Ditambah bonus untuk grafik y = cos (x + 30o) dan y = cos x + 1. Semoga Bermanfaat! Jika ada bagian yang belum paham atau secara tidak sengaja ada bagian yang salah bisa dituliskan pada kolom komentar. Terimakasih.
Baca Juga: Cara Menentukan Nilai Maksimum dan Minimum Suatu Fungsi Trigonometri


Gambar grafik dri y= a)3 cos (2x+180)
b) y= sin(2x+90)
illla ma kuntum ta’lamun
Cara menggambar y= cos x-1