Statistik deskriptif merupakan analisis data mentah dari suatu populasi atau sampel ke dalam bentuk ringkas. Hasil eksplorasi data melalui analisis statistik deskriptif memungkinkan seseorang untuk melihat bagaimana karakteristik suatu data yang diolah. Cakupan eksplorasi data pada analisis statistik deskriptif mencakup penyajian secara numerik dan visualisasi,
Penyajian numerik berupa perhitungan nilai-nilai statistik berupa ukuran pemusatan, penyebaran, letak, dan distribusi data. Sementara visualisasi data dapat berbentuk diagram (chart) bar/batang, garis, pie, atau bentuk chart menarik lainnya. Dari analisis statistik deskriptif selanjutnya berguna untuk digunakan sebagai bahan presentasi atau melakukan analisis data lebih lanjut.

Apa saja yang dilakukan pada eksplorasi analisis data dengan statistik deskriptif? Bagaimana cara melakukan olah data atau analisis statitik deskriptif? Cari tahu jawabannya melalui ulasan langkah kerja dan contoh analisis statistik deskriptif pada ulasan di bawah.
Baca Juga: Perbedaan Statistik Deskriptif dan Inferensial
Daftar isi:
- Eksplorasi Data pada Analisis Statistik Deskriptif
- Cara Membaca/Interpretasi Nilai Hasil Analisis Statistik Deskriptif
Eksplorasi Data pada Analisis Statistik Deskriptif
Eksplorasi data pada analisis data statistik deskriptif secara numerik dilakukan dengan menampilkan nilai-nilai statistik. Beberapa nilai statisik yang ditampilkan antara lain termasuk ukuran pemusatan data dan ukuran keragaman data.
Ukuran pemusatan data mencakup nilai mean (rata-rata), median (nilai tengah), dan modus (data dengan frekuensi terbesar).
- Mean: rata-rata data yang diperoleh dari jumlah semua data dibagi banyak data (frekuensi)
- Median: nilai tengah dari data yang sudah diurutkan terlebih dahulu nilainya
- Modus: data dengan frekuensi terbesar atau data yang paling sering muncul
Sementara ukuran keragaman data mencakup nilai range (jangkauan), kuartil, varians (ragam), dan standar deviasi (simpangan baku), skewness (koefisien kecondongan) , dan kurtosis (keruncingan kurva).
- Range (jangkauan): seberapa jauh sebaran data dengan melihat nilai selisih data tertinggi/terbesar dengan data terendah/terkecil.
- Kuartil: nilai pembatas yang membagi data menjadi empat bagian sama banyak
- Varians (ragam): ukuran sebarapa jauh penyebaran data dari nilai rata-rata, semakin kecil nilai variansi menunjukkan data semakin dekat dengan rata-rata
- Standar deviasi (simpangan baku): memberikan ukuran yang lebih tepat untuk menentukan penyebaran data terhadap rata-rata
- Skewness (Sk) atau koefisien kecondongan: ukuran ketidaksimetrisan data melalui kemencengan data terhadap rata-rata
Sk > 0 → menceng kanan (positif)
Sk = 0 → kurva normal
Sk < 0 → menceng kiri (negatif) - Kurtosis (keruncingan kurva): ukuran keruncingan data yang dapat dinyatakan dalam 3 kondisi yaitu distribusi normal (kurtosis = 3), distribusi leptokurtic atau lebih runcing (kurtosis > 3), dan distribusi platikurtik atau cenderung lebih rata (kurtosis < 3).
Eksplorasi analisis data pada analisis deskriptif dapat dilakukan secara manual atau otomatis menggunakan software. Untuk pengerjaan manual dapat dilakukan dengan perhitungan menggunakan rumus-rumus yang sesuai. Setiap nilai-nilai statistik memiliki rumus yang berbeda untuk mendapatkannya.
Baca Juga:
1) Rumus Mean, Median, Modus
2) Rumus Variansi/Ragam
3) Cara Hitung dan Rumus Kuartil Bawah, Atas, dan Tengah
Untuk pengerjaan secara otomatis dapat menggunakanbantuan perangkat lunak (software) untuk mengolah data seperti SPSS, Microsoft Excel, R, dan lain sebagainya. Dengan menggunakan salah satu perangkat lunak tersebut dapat diperoleh langsung hasilnya berupa nilai-nilai statistik yang dibutuhkan pada analisis deskriptif.
Sebagai contoh, tabel di bawah adalah data inflasi umum di Indonesia pada tahun 2019 berikut. Data pada tabel di bawah akan dijadikan contoh bagaimana cara melakukan eksplorasi data pada analisis deskriptif.

Baca Juga: Penyajian Data dalam Bentuk Boxplot dan Cara Membacanya
Cara Membaca/Interpretasi Nilai Hasil Analisis Statistik Deskriptif
Visualisasi data dan analisis statistik deskriptif menggunakan Google Spreadsheet memberikan hasil nilai-nilai statistik yang dibutuhkan pada anlisis statistik deskriptif. Google Spreadsheet sendiri memiliki cara kerja yang sangat mirip dengan Microsoft Excel.
Kelebihannya, Google Spreadsheet salah satunya adalah dapat digunakan secara legal tanpa harus berlangganan atau membayar produknya. Sementera kekurangan Google Spreadsheet membutuhkan koneksi internet untuk memulai pemakaiannya dan memanfaatkan semua fiturnya menjadi secara optimal.
Berikut ini adalah hasil analisis statistik deskriptif yang dilakukan secara otomatis menggunakan Google spreadsheet.
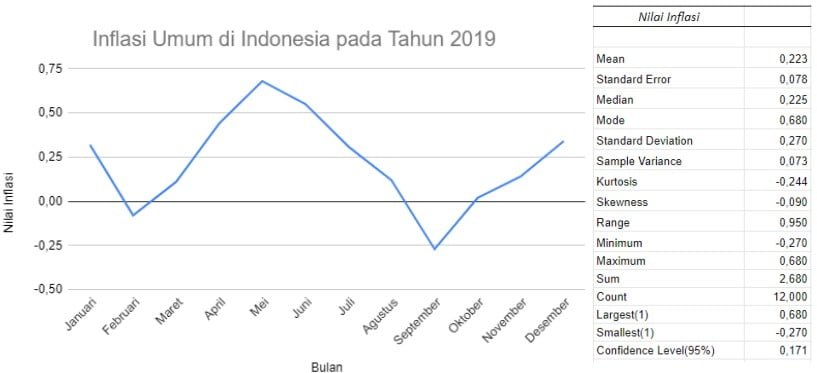
Gambar di sebelah kanan menampilkan bentuk data inflasi dalam bentuk diagram garis. Sedangkan tabel di sebelah kanan menampilkan nilai-nilai statistik penting dalam analisis statistik deskriptif.
Setiap nilai hasil analisis deskriptif dapat menggambarkan bagaimana karakteristik dari data yang diolah. Berikut ini adalah contoh cara membaca dan interpretasi nilai hasil analisis statistik deskriptik untuk data inflasi umum di Indonesia pada tahun 2019.
Ukuran pemusatan data dilihat dari nilai mean, median, dan modus.
Rata-rata inflasi umum di Indonesia pada tahun 2019 sama dengan yang ditunjukkan dari angka mean = 0,223. Nilai tengah inflasi pada tahun 2019 sama dengan nilai median = 0,225. Sementara nilai inflasi umum dengan frekuensi tertinggi sepanjang tahun 2019 sama dengan nilai modus = 0,68. Namun jika diamati lagi, nilai modus tersebut bukan nilai dengan frekuensi tertinggi nilai dari kedua belas data berbad. Nilai modus merupakan nilai tertinggi dari data tersebut.
Untuk ukuran keragaman dapat dilihat dari nilai range (jangkauan), standard deviataion (simpangan baku) dan sample variance (variansi sampel). Untuk bentuk kurva distribusi data dapat dilihat dari nilai kurtosis dan skewnees.
- Range = 0,95 → selisih inflasi tertinggi dan terendah di tahun 2019 adalah 0,95
- Standard deviation = 0,270 → sampel yang kita gunakan tersebar dekat dari rata-rata
- Sample variance = 0,073 → sampel yang kita gunakan tersebar dekat dari rata-rata
- Kurtosis = -0,244 → sampel memiliki distribusi platikurtik (cenderung rata) karena karena nilai kurtosis lebih kecil dari tiga
- Skewness = -0.090 → sampel data yang kita gunakan cenderung menceng kiri
Demikianlah tadi contoh cara melalukan olah data dan analisis statistik deskriptif. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Peluang Kejadian Majemuk dan Bersyarat