Materi perpangkatan dan bentuk akar kelas 9 berkaitan dengan cara melakukan perhitungan bilangan dengan bentuk pangkat dan akar. Contoh bilangan berpangkat adalah 23, 32, 53, dan lain sebagainya. Sementara contoh bilangan bentuk akar adalah √2, √3, √5, dan lain sebagainya.
Dalam operasi perpangkatan dan bentuk akar kelas 9 terdapat aturan yang berlaku untuk melakukan operasi hitung. Apa yang dipelajari pada materi perpangkatan dan bentuk akar kelas 9 adalah melakukan operasi hitung 23 + 23, 23 − 22, √28 + √50, √28 − √50, atau yang lainnya.
Tentunya operasi perhitungan dilakukan tanpa bantuan alat hitung seperti kalkulator, aplikasi ponsel, atau perangkat lunak komputer.
Baca Juga: Operasi Hitung Aljabar
Bagaimana cara melakukan operasi hitung perpangkatan dan bentuk akar? Sobat idschool dapat mencari tahu jawabannya melalui ulasan perpangkatan dan bentuk akar kelas 9 di bawah.
Daftar isi:
Aturan Operasi Hitung Bilangan Perpangkatan
Hasil nilai suatu bilangan berpangkat dihitung dengan mengalikan bilangan yang sama sebanya bilangan pangkatnya. Contohnya pada bilangan berpangkat 23. Cara menghitungnya adalah 23 = 2×2×2 = 8. Contoh lain untuk 32, nilainya sama dengan 32 = 3×3 = 9.
Perhatikan bahwa perhitungan dilakukan dengan mengalikan bilangan yang sama sebanyak bilangan pangkatnya. Secara umum operasi perpangkatan an sama dengan pekalian a dengan a sebanyak n kali.

Dalam operasi hitung perpangkatan terdapat aturan atau sifat operasi yang berlaku. Beberapa sifat operasi tersebut terdapat pada daftar di bawah.
- a0 = 1
- am × an = am+n
- am : an = am–n
- (am)n = amn
- (a × b)n = an × bn
- (a : b)n = an : bn
- Pangkat negatif:
Baca Juga: Cara menentukan satuan bilangan yang berpangkat banyak, contoh: satuan dari 22023?
Aturan Operasi Hitung Bilangan Bentuk Akar
Dalam melakukan operasi hitung bilangan bentuk akar juga terdapat aturan yang berlaku. Aturan tersebut banyak memiliki kemiripan dengan operasi hitung aljabar biasa.
Contohnya pada penjumlahan aljabar bilangan dengan variabel x + 2x = 3x. Untuk penjumlahan bilangan bentuk akar √2 + 2√2 = 3√2. Perhitungan yang dilakukan untuk kedua bentuk penjumlahan tersebut dilakukan dengan menjumlahkan bilangan bulat di depan.
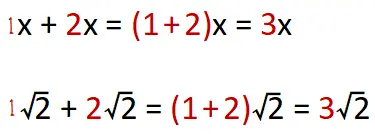
Operasi hitung bentuk akar tidak hanya sebatas penjumlahan. Bentuk operasi hitung dapat juga berupa pengurangan, perkalian, dan pembagian. Selain itu ada juga operasi pada bilangan dengan pangkat pecahan, menyederhanakan bentuk akar, dan merasionalkan bentuk akar.
Bentuk sifat operasi hitung bilangan perpangkatan dan bentuk akar kelas 9 meliputi beberapa aturan berikut.
1) Penjumlahan dan Pengurangan Bentuk Akar
Penjumlahan dan pengurangan bentuk akar dapat dilakukan pada bilangan yang memiliki bilangan yang sama di dalam tanda akar. Untuk dua bilangan dengan bentuk akar yang berbeda tidak bisa dilakukan penjumlahan atau pengurangan.
Operasi penjumlahan dapat dilakukan untuk menjumlahkan m√a + n√a. Namun tidak dapat digunakan untuk menjumlahkan m√a + n√b. Begitu juga untuk operasi pengurangan berlaku aturan yang sama.
Aturan operasi penjumlahan dan pengurangan bentuk akar:
- m√a + n√a = (m+n)√a
Contoh:
3√2 + 2√2 = (3+2)√2 = 5√2
2√3 + √3 = (2+1)√3 = 3√3
2√3 + √2 = tidak dapat dijumlah
- m√a – n√a = (m – n)√a
Contoh:
3√2 – 2√2 = (3–2)√2 = √2
2√3 – √3 = (2–1)√3 = √3
2√3 – √2 = tidak dapat dikurang
2) Perkalian dan Pembagian Bentuk Akar
Perkalian bentuk akar dilakukan dengan mengalikan bilangan di luar tanda akar dengan bilangan di luar tanda akar juga. Sementara untuk bilangan di dalam tanda akar dikalikan dengan bilangan di dalam tanda akar. Begitu juga untuk operasi pembagian, aturan untuk perkalian berlaku juga dalam pembagian bentuk akar.
Aturan operasi perkalian dan pembagian bentuk akar:
- m√a × n√b = (m×n)√a
Contoh:
3√2 × 2√3 = (3×2)√(2×3) = 6√6
2√3 × √5 = (2×1)√(3×5) = 2√15
- m√a : n√b = (m : n)√(a : b)
Contoh:
6√2 : 2√2 = (6:2)√(2:2) = 3√1 = 3
2√3 – √3 = (2–1)√3 = √3
3) Mengubah Pangkat Pecahan ke Bentuk Akar
Bilangan dengan pangkat pecahan memiliki bentuk ekuivalen dengan bilangan bentuk akar. Dengan bentuk ekuivalen tersebut, nilai bilangan dengan pangkat pecahan dapat dicari tahu nilainya.
Pada bilangan dengan pangkat pecahan, penyebut pecahan menjadi akar pangkat dan pembilangnya menjadi pangkat bilangan. Untuk bilangan a dengan pangkat pecahan m/n sama dengan akar n dari a pangkat m.
am/n = n√am
Contoh:
1.) 81/3 = 3√8 = 2
2.) 91/2 = √9 = 3
3.) 82/3 = 3√82 = 3√64 = 4
4) Menyederhanakan Bentuk Akar
Operasi menyederhanakan bentuk akar dibutuhkan untuk mencari bentuk akar yang paling sederhana. Bentuk operasi menyederhanakan bentuk akar menggunakan aturan perkalian bentuk akar.
Pada aturan perkalian bilangan dalam akar berlaku √(a×b) = √a×√b. Untuk perkalian bilangan dalam akar √(a2×b) = √a2×√b = a×√b = a√b.
Contohnya pada bilangan irasional √32, di mana bilangan 32 dapat dinyatakan dalam perkalian 16×2. Sehingga √32 = √(16×2) = √16 × √2 = 4√2.

Dalam menyederhanakan bentuk akar, penting untuk membuat perkalian bilangan dalam akar dengan salah satu bilangan yang dapat ditari nilai akarnya. Bilangan yang dapat ditarik akar dua adalah semua bilangan kuadrat seperti 1, 4, 9, 16, 25, dan lain sebaginya (rumus: n2).
5) Merasionalkan bentuk akar
Merasionalkan bentuk akar umumnya dilakukan pada pecahan yang memiliki penyebut dengan bilangan bentuk akar. Cara merasionalkan bentuk akar dilakukan dengan mengalikan akar sekawan.
Akar sekawan adalah bentuk akar yang akan membuat pasangan bentuk akarnya menjadi bilangan rasional. Contoh pasangan bentuk akar dan akar sekawan terdapat pada tabel berikut.
| Bentuk Akar | Akar Sekawan |
| √a | √a |
| a√b | a√b |
| a + √b | a − √b |
| √a + √b | √a − √b |
Cara merasionalkan bentuk akar terdapat pada tiga contoh dengan mengambil bentuk umum seperti berikut.
Baca Juga: Operasi Hitung Positif Negatif Bilangan Bulat
Ringkasan Sifat Perpangkatan dan Bentuk Akar Kelas 9
Rumus-rumus yang dapat digunakan untuk melakukan operasi hitung perpangkatan dan bentuk akar kelas 9 terdapat pada aturan-aturan berikut.
Baca Juga: Perbandingan Senilai dan Berbalik Nilai
Contoh Soal Perpangkatan dan Bentuk Akar Kelas 9
Beberapa soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan materi perpangkatan dan bentuk akar kelas 9 di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 Operasi Hitung Perpangkatan
Hasil dari 46 : (32×16) = ….
A. 221
B. 211
C. 25
D. 23
Pembahasan:
Operasi pembagian dan perkalian pada soal akan lebih mudah dilakukan dengan mengetahui cara melakukan operasi perpangkatan dan bentuk akar kelas 9 pada pembahasan di atas.
Bagaimana cara menentukan hasil dari 46 : (32×16) terdapat pada penyelesaian di bawah.
Menghitung 46 : (32 × 16)
= (22)6 : (25 × 24)
= 212 : (25 × 24)
= 212 : 25+4
= 212 – 9
= 23
Jadi, hasil dari 46 : (32 x 16) = 23
Jawab: E
Contoh 2 Soal Menyederhanakan Bentuk Akar
Hasil dari √48 + 2√27 − √147 adalah ….
A. √3
B. 2√3
C. 3√3
D. 4√3
Pembahasan:
Hasil dari penjumlahan dan pengurangan bentuk akar dapat dilakukan saat bilangan di dalam tanda akar sama.
Untuk itu perlu membuat bilangan-bilangan bentuk akar tersebut menjadi bentuk akar yang memiliki bilangan sama di dalam tanda akar.
Menentukan hasil √48 + 2√27 − √147
= √(16×3) + 2√(9×3) − √(49×3)
= √16 × √3 + 2 × √9 × √3 − √49 × √3
= 4√3 + 2 × 3√3 − 7√3
= 4√3 + 6√3 − 7√3
= (4 + 6 − 7)√3 = 3√3
Jadi, hasil dari √48 + 2√27 − √147 adalah 3√3.
Jawaban: C
Demikianlah tadi ulasan aturan operasi yang berlaku pada perpangkatan dan bentuk akar kelas 9. Terima kasih sudah mengunjungi idshcool(dot)net, semoga bermanfaat!

