Jarak titik ke garis sama dengan panjang ruas garis terpendek yang menghubungkan titik dengan garis. Cara menentukan jarak titik ke garis dilakukan dengan melakukan proyeksi titik pada garis. Panjang garis yang menghubungkan titik dengan proyeksi titik tersebut pada garis sama dengan jarak titik ke garis.
Ruas garis yang menghubungkan titik ke titik proyeksi disebut garis proyektor. Sifat garis proyektor adalah tegak lurus terhadap garis yang memuat titik proyeksi.
Jarak titik garis sama dengan panjang garis proyektor. Cara menghitung panjang garis proyektor dapat menggunakan berbagai rumus seperti Teorema Pythagoras, Aturan Cosinus, dan Luas Segitiga.
Bagaimana cara menghitung jarak titik ke garis? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Menentukan Ruas Garis yang Menjadi Jarak Titik ke Garis
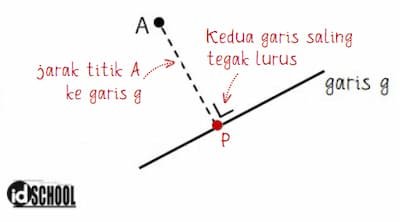
Sebuah titik A terletak di luar garis g. Cara menentukan jarak titik A ke garis g dilakukan dengan melakukan proyeksi titik A pada garis g terlebih dahulu. Misalkan hasil proyeksi titik A ke garis g adalah titik P.
Sebuah ruas garis yang diperoleh dengan menghubungkan titik A ke titik P adalah garis AP. Ruas garis AP tersebut akan tegak lurus dengan garis g. Di mana ruas garis AP dan garis g memiliki hubungan saling tegak lurus, Jarak titik A ke garis g sama dengan panjang ruas garis AP.
Langkah menentukan mana ruas garis yang menjadi jarak titik ke sebuah garis penting untuk diketahui agar tidak salah menentukan panjang ruas garisnya. Untuk menentukan panjang ruas garis yang menjadi jarak titik ke sebuah garis memiliki banyak cara, bergantung dari ruas garis yang akan dihitung panjangnya.
Baca Juga: Pasangan Garis Saling Sejajar, Berpotongan dan Bersilangan pada Kubus ABCD EFGH
Cara Menghitung Jarak Titik ke Garis
Setelah mengetahui mana ruas garis yang menjadi jarak titik garis, perhitungan perlu dilakukan untuk mengetahui panjang ruas garis tersebut. Beberapa soal di bawah menunjukkan cara bagaimana cara menentukan dan menghitung jarak titik garis.
Soal 1: Sebuah kubus ABCD.EFGH yang mempunyai panjang rusuk 6 cm. Tentukan jarak titik A dan garis EF!
Jawab:
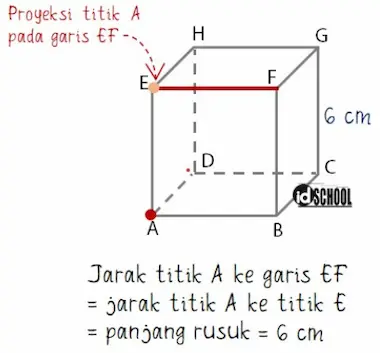
Proyeksi titik A pada garis EF adalah titik E. Sehingga jarak titik A ke garis EF sama dengan jarak titik A ke titik E yaitu ruas garis AE.
Diketahui bahwa ruas garis AE merupakan rusuk kubus. Sehingga, jarak titik A ke garis EF sama dengan panjang rusuk kubus yaitu AE = 6 cm.
Soal 2: Diketahui kubus ABCD.EFGH yang mempunyai panjang rusuk 12 cm, jarak titik C ke garis AG adalah ….
Jawab:
Misalkan proyeksi titik C pada garis AG adalah P. Maka jarak titik C ke garis AG sama dengan panjang ruas garis CP.
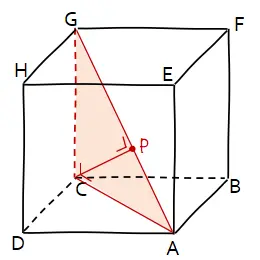
Pada sebuah kubus, panjang diagonal bidang = rusuk√2 dan panjang diagonal ruang = rusuk√3. Pada kubus ABCD.EFGH di atas, garis AG adalah diagonal ruang dan garis AC adalah diagonal bidang. Sehingga panjang AG dan AC berturut-turut adalah AG = 6√3 dan AC = 6√2.
Berikutnya perhatikan segitiga ACG!
Segitiga ACG dapat dipandang dengan dua cara. Pertama adalah segitiga dengan alas AC dan tinggi CG. Kedua adalah segitiga dengan alas AG dan tinggi CP.
Menghitung panjang ruas garis CP:
12 × 12√2 = 12√3 × CP
√3CP = 12√2
CP = 12√2/√3 × √3/√3
CP = 12√6/3 = 4√3 cm
Jadi, jarak titik C ke garis AG adalah CP = 4√3 cm.
Baca Juga: Cara Menghitung Jarak Garis ke Garis
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan yang diberikan untuk mengukur keberhasilan mengerjakan soal dan tingkat pemahaman materi. Selamat berlatih!
Contoh 1 – Soal Jarak Titik ke Garis
Diketahui kubus ABCD EFGH dengan panjang rusuk 6 cm. Jarak titik C ke garis FH adalah ….
A. 2√6 cm
B. 3√6 cm
C. 4√6 cm
D. 5√6 cm
E. 6√6 cm
Pembahasan:
Antara titik C dan dua titik pada garis FH dapat dihubungkan sehingga tersebut sebuah segitiga CFH seperti berikut.

Perhatikan segitiha FCH memiliki panjang sisi yang sama yaitu CH = CF = FH = diagonal bidang = 6√2 cm. Ketiga sisi segitiga sama besar, sehingga segitiga tersebut merupakan segitiga sama sisi. Besar ketiga sudut pada segitiga sama sisi adalah sama besar yaitu 60o.
Selanjutnya perhatikan segitiga COF. Perbandingan sisi depan (CO) dan sisi miring (FC) pada segitiga CFO sama dengan nilai sin 60o. Panjang CO dapat dicari dari persamaan fungsi trigonometri tersebut.
Menghitung panjang CO:
CO/FC = sin 60o
CO = FC × sin 60o
CO = 6√2 × 1/2√3
CO = 3√6 cm
Jadi, jarak titik C ke garis FH pada kubus ABCD.EFGH dengan panjang rusuk 6 cm adalah CO = 3√6 cm.
Jawaban: B
Contoh 2 – Soal Jarak Titik ke Garis
Kubus ABCD.EFGH mempunyai panjang rusuk 12 cm. Titik T merupakan perpotongan antara diagonal EG dan FH.
Jarak titik A ke ruas garis CT adalah ….
A. 12√3 cm
B. 12√2 cm
C. 8√6 cm
D. 8√3 cm
E. 8√2 cm
Pembahasan:
Misalkan proyeksi titik A ke garis CT adalah titik P, jarak titik ke garis CT sama dengan panjang ruas garis AP.
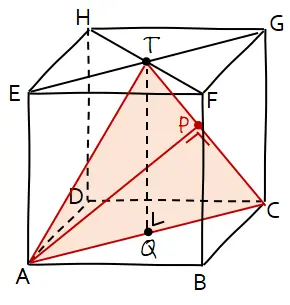
Dari soal diketahui bahwa panjang rusuk kubus ABCD.EFGH adalah 12 cm.
Sehingga,
- Panjang diagonal bidang = rusuk√2
AC = 12√2 cm - TG = ½ × panjang diagonal bidang
TG = ½ × 12√2 = 6√2 cm - TQ = panjang rusuk kubus
TQ = 12 cm
Dari segitiga CGT dapat dihitung panjang CT menggunakan Teorema Pythagoras.
Menghitung panjang CT:
CT2 = TG2 + CG2 = (6√2)2 + 122
CT2 = 72 + 144 = 216
CT = √(36×6) = 6√6 cm
Selanjutnya perhatikan segitiga ACT. Segitiga tersebut dapat dipandang dengan dua cara. Pertama adalah segitiga dengan alas CT dan tinggi AP. Kedua adalah segitiga dengan alas AC dan tinggi TQ.
Panjang AP dapat dihitung seperti langkah penyelesaian berikut.
Menghitung panjang AP:
L ΔACT = L ΔACT
6√6 × AP = 12√2 × 12
6√6 × AP = 144√2
AP = 144√2/6√6 = 24√2/√6
Menyederhanakan bilangan AP:
AP = 24√2/√6 × √6/√6
AP = 24√12/6 = 4√12
AP = 4 × √(4×3)
AP = 4 × √4 × √3
AP = 4 × 2 × √3 = 8√3 cm
Jadi, jarak titik A ke ruas garis CT adalah AP = 8√3 cm.
Jawaban: D
Sekian pembahasan mengenai jarak titik ke garis pada dimensi tiga. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga Dimensi Tiga: Jarak Titik ke Bidang