Kubus adalah salah satu bentuk bangun ruang bangun datar yang cukup mudah dikenali. Di mana terdapat 6 buah sisi berbentuk persegi dan 12 rusuk berupa ruas garis. Setiap kubus ABCD.EFGH terdapat pasangan garis saling sejajar, berpotongan, dan bersilangan. Setiap satu bidang pada kubus sejajar dengan satu bidang lain sehingga ada tiga pasang bidang yang saling sejajar.
Kubus ABCD.EFGH memiliki 6 sisi yang memiliki bentuk sama berupa persegi. Banyaknya rusuk dalam kubus ABCD.EFGH berjumlah 12 yang panjangnya sama.
Bangun ruang berbentuk kubus memiliki 2 macam diagonal yaitu diagonal sisi dan diagonal ruang. Banyak diagonal sisi kubus sama dengan dua kali sisi kubus yaitu 12 diagonal sisi. Sedangkan banyak diagonal ruang kubus sama dengan 4 diagonal ruang.
Gambaran bangun ruang berbentuk kubus beserta keterangan bangian-bagiannya diberikan seperti gambar berikut.
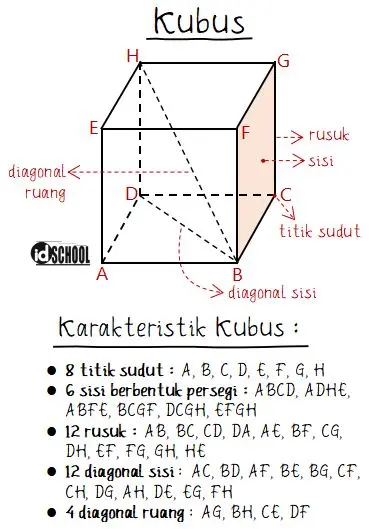
Baca Juga: Rumus Volume Kubus
Mana saja pasangan garis saling sejajar pada kubus ABCD-EFGH? Apa saja pasangan garis yang saling berpotongan dan bersilangan? Sobat idcshool dapat mencari tahu jawaban mana saja garis saling sejajar, berpotongan, dan bersilangan pada kubus ABCD-EFGH melalui ulasan di bawah.
Daftar isi:
Pasangan Garis Saling Sejajar, Berpotongan, dan Bersilangan
Sebelumnya sobat idschool perlu mengetahui bagaimana dua garis dikatakan saling sejajar, berpotongan, dan bersilangan. Dari definisi tersebut, selanjutnya sobat idschool dapat menentukan pasangan garis saling sejajar, berpotongan, dan bersilangan pada suatu kubus.
Dua buah garis dikatakan saling sejajar jika kedua garis tidak memiliki titik potong. Untuk dua garis saling berpotongan terdapat pada dua buah garis yang memiliki satu titik potong. Biasanya, dua buah garis yang saling sejajar dan berpotongan terdapat pada bidang datar yang sama.
Contoh pasangan garis yang saling sejajar pada kubus ABCD.EFGH adalah AB dan EF. Sedangkan contoh pasangan garis yang saling berpotongan adalah DC dam GC.

Sedangkan dua buah ruas garis dikatakan saling bersilangan jika garis-garis tersebut terletak di bidang yang berbeda. Dua garis yang saling bersilangan tidak memiliki titik potong.
Selain pasangan garis saling sejajar, berpotongan, dan bersilangan terdapat juga garis yang saling berimpit. Dua garis yang saling berimpit terletak pada satu garis lurus sehingga hanya terlihat sebagai satu garis.

Baca Juga: Materi Pengantar Dimensi Tiga (Bangun Ruang)
Daftar Pasangan Garis Saling Sejajar, Berpotongan, dan Bersilangan
Perhatikan kubus ABCD.EFGH dengan 12 rusuk yaitu AB, BC, CD, DA, AE, BF, CG, DH, EF, FG, GH, dan HE berikut.

Pada kubus ABCD-EFGH di atas terdapat pasangan garis saling sejajar, berpotongan, dan bersilangan. Banyak pasangan garis saling sejajar, berpotongan, dan bersilangan berturut-turut adalah 18, 24, dan 24. Daftar pasangan garis saling sejajar, berpotongan, dan bersilangan terdapat pada daftar berikut.
Daftar pasangan garis saling sejajar pada kubus ABCD-EFGH:
- AB // CD;
- AB // GH;
- AB // EF;
- CD // EF;
- CD // GH;
- GH // EF;
- AE // BF;
- AE // CG;
- AE // DH;
- BF // CG;
- BF // DH;
- CG // DH;
- AD // BC;
- AD // FG;
- AD // EH;
- BC // FG;
- BC // EH;
- FG // EH
Daftar pasangan garis saling berpotongan kubus ABCD-EFGH:
- AD dan BC;
- AD dan CD;
- EF dan FG;
- EH dan GH;
- AB dan AD;
- BC dan CD;
- EF dan EH;
- EH dan GH;
- AB dan BF;
- AE dan EF;
- BF dan EF;
- AB dan AE;
- BC dan CG;
- BC dan BF;
- CG dan FG;
- BF dan FG;
- CD dan CG;
- CD dan DH;
- CG dan GH;
- DH dan BH;
- AD dan DH;
- AE dan EH;
- AD dan AE;
- DH dan EH
Daftar pasangan garis saling bersilangan pada kubus ABCD-EFGH:
- AB dan FG;
- AB dan EH;
- AB dan CG;
- AB dan DH;
- AD dan EF;
- AD dan GH;
- AD dan BF;
- AD dan CG;
- AE dan BC;
- AE dan FG;
- AE dan CD;
- AE dan BH;
- BC dan DH;
- BC dan EF;
- BC dan GH;
- BF dan EH;
- BF dan CD;
- BF dan GH;
- CG dan EG;
- CG dan EH;
- CD dan FG;
- CD dan EH;
- DH dan EF;
- DH dan FG
Baca Juga: [Dimensi Tiga] Jarak Garis ke Bidang pada Bangun Ruang
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan bagaimana pasangan garis saling sejajar, berpotongan, dan bersilangan pada kubus ABCD-EFGH. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Menentukan Kedudukan Suatu Garis Terhadap Garis Lain

Contoh 2 – Soal Pasangan Garis Saling Sejajar, Berpotongan, dan Bersilangan
Perhatikan gambar kubus ABCD.EFGH di bawah!

Pasangan garis yang saling bersilangan adalah ….
A. AB dan GH
B. BC dan CD
C. AE dan CG
D. DH dan EF
Pembahasan:
Dua buah garis dikatakan bersilangan jika kedua garis terletak pada bidang yang berbeda dan tidak memiliki titik potong. Hubungan 2 garis yang terdapat pada pilihan jawaban adalah sebagai berikut.
- AB dan GH: sejajar
- BC dan CD: berpotongan
- AE dan CG: sejajar
- DH dan EF: bersilangan
Jadi, pasangan garis yang saling bersilangan adalah DH dan EF.
Jawaban: D
Baca Juga: Rumus 4 Macam Bangun Ruang Sisi Datar dan Karakteristiknya
Contoh 3 – Soal Pasangan Garis Saling Sejajar, Berpotongan, dan Bersilangan

Pembahasan:
Dua buah garis bersilangan terdapat pada 2 garis yang terletak pada bidang yang berbeda dan tidak memiliki titik potong. Garis pertama bersilangan tegak lurus dengan garis kedua jika terdapat pada garis ketiga yang sejajar garis pertama dan tegak lurus garis kedua. Sehingga, garis yang bersilangan tegak luru adalah BD dan AE.
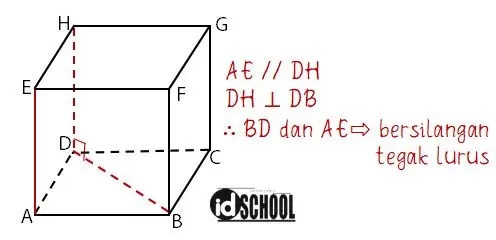
Jadi, pasangan garis yang saling bersilangan tegak lurus adalah BD dengan AE.
Jawaban: D
Contoh 4 – Soal Pasangan Garis Saling Sejajar, Berpotongan, dan Bersilangan
Perhatikan gambar kubus berikut!

Pasangan garis dan bidang yang sejajar adalah ….
A. AB dan BCGF
B. AD dan EFGH
C. CG dan ABCD
D. EH dan CDHG
Pembahasan:
Garis dan bidang dikatakan sejajar jika garis berada pada suatu bidang yang sejajar dengan bidang tersebut. Ruas garis AD berada pada bidang ABCD, di mana bidang ABCD sejajar EFGH. Sehingga, hubungan garis AD dan EFGH adalah sejajar.
Jadi, pasangan garis dan bidang yang sejajar adalah AD dan EFGH.
Jawaban: B
Demikianlah tadi ulasan pasangan garis saling sejajar, berpotongan, dan bersilangan pada kubus ABCDEFGH. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Materi Jarak pada Dimensi Tiga
