Ada 10 contoh soal PK UTBK SNBT 2024 dari simulasi-tes.bppp.kemdikbud.go.id untuk peserta ujian. Soal PK (Pengetahuan Kuantitatif) dari halaman tersebut telah disalin di bawah. Tentunya dengan pembahasan yang lebih jelas. Kesepuluh contoh soal PK UTBK SNBT 2024 adai di bawah.
Daftar isi:
- Soal 1: Nilai minimum fungsi kuadrat
- Soal 2 – 4:
- Soal 5: Perhatikan kumpulan data b, –11, 3, –5
- Soal 6: Segi empat ABCD adalah belah ketupat
- Soal 7: Tiga bilangan asli berbeda yang kurang dari 10 dipilih …
- Soal 8: Segitiga ABC siku-siku dengan …
- Soal 9: Perhatikan barisan bilangan real 2, a, 8, ….
- Soal 10: Fungsi f didefinisikan dengan f(x) = x2 – 3x …
Soal 1: Nilai minimum fungsi kuadrat
Nilai minimum fungsi kuadrat f adalah –8 dan grafik fungsi tersebut melalui titik (–1, 0) dan titik (3, 0). Grafik fungsi tersebut juga melalui titik (4, b) dengan b = ….
(A) 42
(B) 21
(C) 10
(D) 5
(E) 0
Jawab: (C)
Dari soal diketahui:
- Nilai minimum fungsi kuadrat f adalah –8: yp = –8
- Grafik fungsi tersebut melalui titik (–1, 0) dan titik (3, 0) → grafik memotong sumbu x pada dua titik yaitu x1 = –2 dan x2 = 3.
Dari informasi awal yang diberikan dapat diperoleh sumbu simetri atau absis untuk titik puncak yaitu setengah dari jarak titik perpotongan grafik dengan sumbu x. Dua titik perpotongan grafik dengan sumbu x adalah x1 = –2 dan x2 = 3. Sehingga absis dari titik puncak grafik fungsi adalah xp = 1/2(3 – (–1)) = 1/2 × 4 = 2.
Dapat diketahui bahwa titik puncak grafik adalah (1, –8). Gambaran grafik fungsi kuadrat yang sesuai keterangan pada soal nampak seperti berikut.
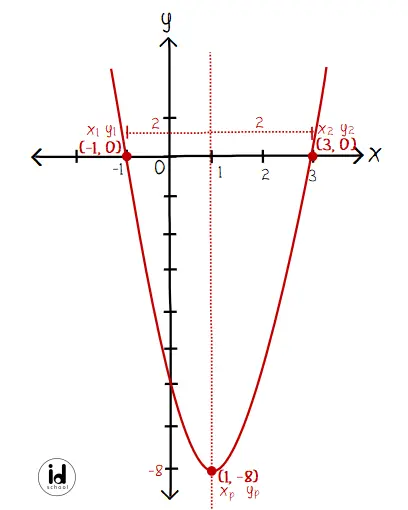
Bentuk umum persamaan fungsi kuadrat: y = a(x – x1)(x – x2)
Diketahui bahwa grafik melalui titik (–1, 0); titik (3, 0); dan titik (1, -8). Persamaan fungsi kuadrat tersebut dapat diketahui dengan cara berikut.
1) Mencari nilai a:
Rumus: yp = a(xp – x1)(xp – x2)
Sehingga,
a(1 + 1)(1 – 3) = –8
a · 2 · (–2) = -8
2) Persamaan grafik fungsi kuadrat:
Rumus yang digunakan: y = a(x – x1)(x – x2)
Sehingga,
y = 2(x – (-1))(x – 3)
= 2(x + 1)(x – 3)
= 2(x2 – 2x – 3) = 2x2 – 4x – 6
Setelah mendapktan persamaan fungsi kuadrat tersebut, selenjutnya dapat dihitung nilai b. Caranya substitusi titik (4, b) ker persamaan fungsi kuadrat tersebut.
Mencari nilai b:
b = 2(4)2 – 4(4) – 6
b = 32 – 16 – 6 = 10
Jadi, grafik fungsi tersebut juga melalui titik (4, b) dengan b = 10 (C).
Soal 2 – 4:
Bilangan empat angka a094 kurang dari 6.000
Soal no 2:
Jika bilangan tersebut dibagi 3 bersisa 1, maka a = ….
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Jawab: (C)
Ciri bilangan habis dibagi 3 adalah jumlah digit-digit bilangan yang menyusunnya habis dibagi tiga.
Bilangan yang diberikan pada soal terdiri dari 4 digit angka yaitu a, 0, 9, dan 4. Diketahui bilangan tersebut sisa satu ketika dibagi tiga. Sehingga kemungkinan jumlah empat digit dari bilangan tersebut adalah 16 (saat a = 3), 19 (saat a = 6), 22 (saat a = 9), dan seterusnya.
Dari soal diketahui bahwa bilangan kurang dari 6.000, sehingga nilai a yang memenuhi adalah a = 3. Bilangan tersebut adalah 3094.
Soal nomor 3:
Banyak faktor prima dari bilangan empat angka tersebut adalah ….
(A) 2
(B) 2
(C) 4
(D) 5
(E) 6
Jawab: (C)
Faktor prima adalah bilangan-bilangan prima yang dapat membagi habis suatu bilangan. Bilangan prima adalah bilangan yang hanya dapat dibagi oleh satu dan bilangan itu sendiri. Himpunan bilangan prima = {2, 3, 5, 7, 11, 13, 17, 19, 23, dan seterusnya}.
Faktorisasi prima untuk 3094 adalah 2×7×13×17, atau bilangan-bilangan prima yang dapat membagi habis 3.094 adalah 2, 7, 13, dan 17 (banyaknya ada empat). Jadi, banyak faktor prima dari bilangan empat angka tersebut adalah 4 (C).
Soal nomor 4
Banyak faktor positif dari bilangan empat angka tersebut adala ….
(A) 17
(B) 16
(C) 15
(D) 14
(E) 4
Jawab: (B)
Faktor positif adalah bilangan bulat positif yang dapat membagi habis suatu bilangan. Faktor positif dari bilangan 3.094 adalah 1, 2, 7, 13, …, 3.094 dengan banyak belum diketahui.
Banyak faktor positif suatu bilangan dapat dihitung menggunakan faktorisasi prima dengan ketentuan seperti berikut.
- Faktosisati prima bilangan A = ap × bq × cr × ds
- Banyak faktor positif untuk bilangan A = (p + 1) × (q + 1) × (r + 1) × (s + 1)
Sehingga,
- Faktosisati prima 3.094 = 2 × 7 × 13 × 17 (semua bilangan prima yang menjadi faktor 3.094 memiliki pangkat 1)
- Banyak faktor positif untuk 3.094 = 2 × 2 × 2 × 2 = 16
Jadi, banyak faktor positif dari bilangan empat angka tersebut adalah 16.
Soal 5: Perhatikan kumpulan data b, –11, 3, –5
Perhatikan kumpulan data b, –11, 3, –5
Pernyataan mana saja yang bernilai benar berdasarkan kumpulan data di atas?
- Rata-rata kumpulan data tersebut –5 jikan b = –11
- Median kumpulan data tersebut –6 jika b = –11
- Modus kumpulan data tersebut –5 jikan b = –5
- Jangkauan kumpulan data tersebut 3 jika b = –8
(A) (1), (2), dan (3) SAJA yang benar
(B) (1) dan (3) SAJA yang benar
(C) (2) dan (4) SAJA yang benar
(D) HANYA (4) yang benar
(E) SEMUA pilihan benar
Jawab: (A)
Rata-rata (mean) untuk data tunggal sama dengan jumlah semua data dibagi banyak data. Ada 4 data yang dikatahi yaitu b, –7, 3, –5.
Rata-rata data jika b = –11:
Median adalah nilai tengah dari data yang telah diurutkan. Empat nilai data yang diberikan adalah b = –7, –7, 3, –5. Data setelah diurutkan menjadi –7, –7, –5, 3.
Nilai median jika b = –7:
Modus adalah data yang sering muncul atau modus adalah data dengan frekuensi tertinggi. Jika b = –5 maka empat datanya adalah –5, –7, 3, –5.
Nilai –5 muncul sebanyak dua kali dan nilai lainnya hanya sekali. Sehingga modus kumpulan data tersebut jika b = –5 adalah Modus = –5.
Jangkauan adalah selisih data dengan nilai tertinggi dengan data dengan nilai terendah. Jika b = –8, kelompok data menjadi –8, –7, 3, –5.
- Nilai terendah: xmin = –8
- Nilai tertinggi: xmaks = 3
- Jangkauan = xmaks – xmin = 3 – (–8) = 11
Sehingga,
- Rata-rata kumpulan data tersebut –5 jikan b = –11 → BENAR
- Median kumpulan data tersebut –6 jika b = –11 → BENAR
- Modus kumpulan data tersebut –5 jikan b = –5 → BENAR
- Jangkauan kumpulan data tersebut 3 jika b = –8 → SALAH, seharusnya jangkauan = 11
Kesimpulan: (1), (2), dan (3) SAJA yang benar
Soal 6: Segi empat ABCD adalah belah ketupat
Segi empat ABCD adalah belah ketupat.
Berdasarkan informasi di atas, berikan tanda √ pada kolom berikut yang benar.
| Pernyataan | Benar | Salah |
| ABCD mempunyai dua pasang sudut berhadapan sama besar | ||
| ABCD mempunyai dua pasang sisi sama panjang | ||
| Kedua diagonal ABCD sama panjang |
Jawab: Benar, Benar, Salah
Bentuk belah ketupat:
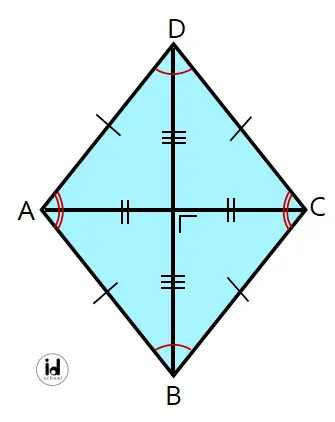
Merangkum dari Cuemath, ciri-ciri belah ketupat meliputi beberapa sifat berikut:
- Sudut-sudut yang berhadapan kongruen atau sama besar.
- Sisi-sisi yang berhadapan sama panjang dan sejajar.
- Diagonal saling membagi dua.
- Jumlah dua sudut yang berdekatan atau berurutan adalah 180°.
ABCD merupakan belah ketupat, sehingga:
- ABCD mempunyai dua pasang sudut berhadapan sama besar → Benar
- ABCD mempunyai dua pasang sisi sama panjang → Benar
- Kedua diagonal ABCD sama panjang → Salah, seharusnya kedua diagonal belah ketupat saling membagi dua.
Jadi, tanda √ pada kolom yang benar secara berurutan terletak pada kolom Benar, Benar, dan Salah.
Soal 7: Tiga bilangan asli berbeda yang kurang dari 10 dipilih …
Tiga bilangan asli berbeda yang kurang dari 10 dipilih sekaligus secara acak.
Berapakah banyaknya dari empat pernyataan berikut yang bernilai benar berdasarkan informasi di atas?
1) Peluang semua bilangan yang terplih prima kurang dari 1/20
2) Peluang semua bilangan yang terpilih genap kurang dari 1/25
3) Peluang semua bilangan yang terpilih ganjil lebih dari 1/7
4) Peluang jumlah semua bilangan yang terpilih kurang dari 8 adalah 1/42
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Jawab: (C)
Bilangan asli kurang dari 10 adalah A = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Banyak cara memilih tiga bilangan asli berbeda secara acak adalah 3C9. Sehingga banyak ruang sampelnya adalah:
A = kejadian terambil tiga bilangan prima
Banyak bilangan prima kurang dari sepuluh adalah Prima = {2, 3, 5, 7}. Banyak cara mengambil tiga angka bilangan prima dari empat bilangan prima yang ada sama dengan 3C4.
P(A) = peluang kejadian terambilnya tiga bilangan prima
B = kejadian terambil tiga bilangan genap
Banyak bilangan genap kurang dari sepuluh adalah Genap = {2, 4, 6, 8}. Banyak cara mengambil tiga angka bilangan prima dari empat bilangan prima yang ada sama dengan 3C4.
P(B) = peluang kejadian terambilnya tiga bilangan genap
C = kejadian terambil tiga bilangan ganjil
Banyak bilangan genap kurang dari sepuluh adalah Ganjil = {1, 3, 5, 7, 9}. Banyak cara mengambil tiga angka bilangan prima dari empat bilangan prima yang ada sama dengan 3C5.
P(C) = peluang kejadian terambilnya tiga bilangan ganjil
D = kejadian terambil jumlah tiga bilangan kurang dari 8
Kemungkinan terambil tiga bilangan dengan jumlah kurang dari 8 adalah pengambilan {(1, 2, 3); (1, 2, 4)}. Sehingga banyak kejadian terambil jumlah tiga bilangan kurang dari 8 adalah n(D) = 2.
P(D) = peluang kejadian terambil jumlah tiga bilangan kurang dari 8
Sehingga,
1) Peluang semua bilangan yang terplih prima kurang dari 1/20 → BENAR,
karena P(A) = 1/21 < 1/20
2) Peluang semua bilangan yang terpilih genap kurang dari 1/25 → SALAH,
karena P(B) = 1/21 > 1/20
3) Peluang semua bilangan yang terpilih ganjil lebih dari 1/7 → SALAH,
karena P(C) = 5/42 < 1/7 = 6/42
4) Peluang jumlah semua bilangan yang terpilih kurang dari 8 adalah 1/42 → BENAR,
karena P(D) = 1/42
Jadi, banyaknya pernyataan yang bernilai benar ada 2 (C).
Soal 8: Segitiga ABC siku-siku dengan …
Segitiga ABC siku-siku dengan ∠A – ∠B = 60o dan ∠C = αo .
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?
| P | Q |
| α | 80 |
(A) P > Q
(B) Q > P
(C) P = Q
(D) Tidak dapat ditentukan hubungan P dan Q
Jawab: (D)
Diketahui bahwa segitiga ABC merupakan segitiga siku-siku. Sehingga salah satu besat sudut segitiga ABC adalah 90o.
Diketahui juga bahwa selisih sudut A dan B adalah ∠A – ∠B = 60o. Nilai-nilai kemungkinanbesar sudut A, sudut B, dan sudut C terdapat pada tabel berikut.
| ∠A | ∠B | ∠C = αo |
| 90o | 60o | 30o |
| 60o | 90o | 30o |
| ∠A | 90o – ∠A | 90o |
Ada dua kemungkinan nilai αo yaitu αo = 30o dan αo = 90o sehingga akan ada kemungkinan nilai P yaitu P = 30 atau P = 90. Di sisi lain, diketahui nilai Q = 80. Nilai P adapat lebih kecil dari Q = 80 (saat P = 30) dan nilai P dapat lebih besar dari Q = 80 (saat P = 90).
Ada dua hubungan kuantitas yang tidak sama. Jadi, hubungan antara kuantitas P dan Q berikut yang benar adalah Tidak dapat ditentukan hubungan P dan Q.
Soal 9: Perhatikan barisan bilangan real 2, a, 8, ….
Perhatikan barisan bilangan real 2, a, 8, ….
Apakah 16 merupakan salah satu suku barisan tersebut?
Putuskan apakah pernyataan (1) dan (2) berikut cukup untuk menjawab pertanyaan tersebut.
1. Barisan tersebut adalah barisan aritmatika
2. Barisan tersebut adalah barisan bilangan positif.
(A) Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
(B) Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
(C) Pernyataan (1) dan (2) cukup untuk menjawab pertanyaan, tetapi salah satu dari keduanya tidak cukup.
(D) Pernyataan (1) ataupun pernyataan (2) SAJA sudah cukup untuk menjawab pertanyaan.
(E) Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
Jawab: (A)
Diketahui barisan bilangan real: 2, a, 8, …
Saat diektahui bahwa barisan tersebut adalah barisan aritmatika (pernyataan 1) maka dapat dibentuk rumus Un dengan mencari bedanya terlebih dahulu.
Beda barisan:
8 – a = a – 2
Sehingga dapat diperoleh rumus Un = 2 + 5(n – 1) = 5n – 3 dengan barisan bilangan yang dibentuk adalah 2, 5, 8, 11, 14, 17, …. Maka pertanyaan apakah 16 merupakan salah satu suku barisan tersebut? dapat dijawab dengan TIDAK.
Saat diketahui barisan tersebut adalah barisan bilangan positif (pernyataan 2), tidak ada informasi pasti yang bisa digunakan untuk mengetahui pola barisan bilangan yang dibentuk. Sehingga informasi dari pernyataan 2 tidak bisa digunakan untuk menjawab pertanyaan yang diberikan.
Kesimpulan: Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
Soal 10: Fungsi f didefinisikan dengan f(x) = x2 – 3x …
Fungsi f didefinisikan dengan f(x) = x2 – 3x.
Jawab:
Demikianlah tadi pembahasan sepuluh contoh soal pengetahuan kuantitatif UTBK SNBT 2024 dari simulasi tes yang diberikan panitia penyelenggara SNPMB. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
